初中數學課堂巧用發展性理答

張紅琴

摘 要：理答就是教師對學生回答問題后的反應和處理。有一種非重要的理答方式就是“發展性理答”，主要分為四類：追問、探問、轉問、反問。初中數學教師要學會巧用這“四問”來提升學生的能力，調動學生的學習積極性，使課堂充滿張力和活力。

關鍵詞：數學課堂；發展性理答；勾股定理

華東師范大學崔允漷教授認為：“理答就是教師對學生回答問題后的反應和處理，理答行為既是一種教學行為，它也是一種評價行為。”理答可以分為好幾種類型，其中有一種非重要的理答方式就是“發展性理答”。

發展性理答是指在學生回答不完整、不正確等情況下再次組織問題，再次進行理答。這種理答屬于較高水平的理答，能引導學生深入思考，促進學生思維發展的理答，主要分為以下四類：追問、探問、轉問、反問。初中數學課堂上教師要巧用這“四問”來提升學生的能力，調動學生的學習積極性。

一、巧用追問，提高學生思維的深度

追問是指對一個學生刨根究底地問，即當學生就某一問題回答后，為引導學生深入思考而創設一些問題，引領學生進入思維的深處。

在“勾股定理的應用”教學中，有這樣的教學片段：

老師提問：如圖1，已知邊長為2的等邊三角形ABC，如何求它的面積？

老師追問：很好。為什么會想到“過點A作AD⊥BC”？

學生回答：因為三角形要求面積，必須要有高，所以想到作高。

老師繼續追問：那么作垂直有沒有起到別的作用？

學生想了想，回答：作垂直還起到了構造直角三角形的作用，在直角三角形ABD中，用勾股定理求出了高AD的長。

老師總結：他說得非常準確，作垂直，不僅得到了三角形的高，還構造出了直角三角形，把三角形ABC轉化為兩個直角三角形，這種數學思想方法叫做“化斜為直”，就是將銳角或鈍角三角形轉化為直角三角形。

在這段教學中老師通過連續追問，使學生自己挖掘到問題的本質，找到解決問題的一般方法，老師只需進行簡單歸納提煉即可。

二、巧用探問，降低學生理解的難度

探問是指當學生由于自身知識有所欠缺、問題本身有一定難度等原因無法回答時，教師通過提問，給予一定的引導，降低思維難度，將問題化繁為簡，化難為易。

在“勾股定理的應用”的教學中，有這樣一道習題：

如圖2，在Rt△ABC中，∠C=90°，AC=12，BC=9，AB的垂直平分線分別交AB、AC于點D、E，求AE、EC的長。

請了一個學生回答，他想不出辦法。

老師探問：看到垂直平分線你能想到什么呢？

學生回答：線段垂直平分線上的點到線段兩端的距離相等，我覺得應該將BE連起來（如圖3），則BE=AE。

老師追問：很好，思路完全正確，你還想到了什么？

學生回答：BE+EC=AC=12，但是接下來還沒想好。

老師沒有放棄，繼續探問：你覺得BE和CE位置上有什么關系嗎？

學生回答：它們都在Rt△BCE中，我想到了，可以用勾股定理列方程，設AE=BE=x，在Rt△BCE中，CE2+ BC2=BE2，則92+（12-x）2=x2，從而算出AE和BE。

在這段教學中，老師兩次運用探問，幫助學生降低了思維難度，最終找到了解決問題的辦法。

三、巧用轉問，增加學生參與的廣度

轉問是指當一個學生回答不準確或者不完整時，轉而問其他學生，讓問題得到更多的討論，使問題得到更好的解決。在“平方差公式”的探索過程中，有這樣的教學片段：

老師提問：如圖4，可以用什么方法計算這個圖形陰影部分的面積？

學生甲答：將它補成一個邊長為a的正方形，減去一個邊長為b的正方形即可，面積為a2-b2。

老師追問：很好，還有別的辦法嗎？

學生甲回答不出。

老師探問：這是一個不規則的圖形，剛才你用“補”的方法求出了它的面積，那么我們除了用“補”的辦法還經常用什么方法求面積呢？

學生甲答：還有“割”的辦法，但具體怎么割我還沒有想好。

老師轉問全班同學：甲同學想到了用補或割的辦法求陰影部分面積，給大家提供了很好的方法和思路，非常好，那么有人想到了其他的辦法嗎？大家可以討論一下。

經過討論，學生乙想到了辦法，回答：如圖5，可以將它分割成兩個全等的梯形，上底是b，下底是a，高是（a-b），所以面積為：

學生丙也想到了方法，回答：如圖6，可以將它分為兩個矩形，然后拼成一個長為（a+b），寬為（a-b）的大矩形，這個矩形的面積為（a+b）（a-b）。

接著老師順勢總結出平方差公式。

在這一教學中老師通過追問、探問甲同學，將問題深入，在甲同學回答不出來后，采用了轉問全班同學的方法，讓這個問題得到學生充分的思考和討論，得出了另外兩種方法。老師通過轉問讓更多的學生積極參與到課堂互動中來，并且學生的思維也更加開闊。

四、巧用反問，增強學生反思的力度

反問是指引導學生進行反思，反過來想想這樣對嗎，進而明確自己答案的不足，這樣比老師直接否定更利于學生接受和和理解。

在勾股定理及其逆定理的教學中，老師出了這樣一道例題讓學生完成：

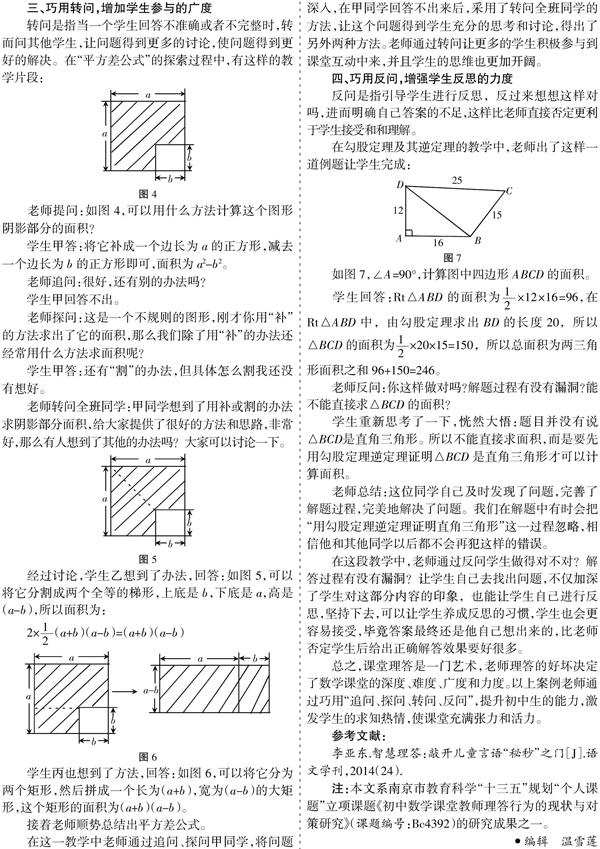
如圖7，∠A=90°，計算圖中四邊形ABCD的面積。

老師反問：你這樣做對嗎？解題過程有沒有漏洞？能不能直接求△BCD的面積？

學生重新思考了一下，恍然大悟：題目并沒有說△BCD是直角三角形。所以不能直接求面積，而是要先用勾股定理逆定理證明△BCD是直角三角形才可以計算面積。

老師總結：這位同學自己及時發現了問題，完善了解題過程，完美地解決了問題。我們在解題中有時會把“用勾股定理逆定理證明直角三角形”這一過程忽略，相信他和其他同學以后都不會再犯這樣的錯誤。

在這段教學中，老師通過反問學生做得對不對？解答過程有沒有漏洞？讓學生自己去找出問題，不僅加深了學生對這部分內容的印象，也能讓學生自己進行反思，堅持下去，可以讓學生養成反思的習慣，學生也會更容易接受，畢竟答案最終還是他自己想出來的，比老師否定學生后給出正確解答效果要好很多。

總之，課堂理答是一門藝術，老師理答的好壞決定了數學課堂的深度、難度、廣度和力度。以上案例老師通過巧用“追問、探問、轉問、反問”，提升初中生的能力，激發學生的求知熱情，使課堂充滿張力和活力。

參考文獻：

李亞東.智慧理答：敲開兒童言語“秘秒”之門[J].語文學刊，2014（24）.

注：本文系南京市教育科學“十三五”規劃“個人課題”立項課題《初中數學課堂教師理答行為的現狀與對策研究》（課題編號：Bc4392）的研究成果之一。