HPM視角下反證法的教學設計研究

張艷蓉　張府柱

摘? 要：該文從數學史融入數學教學的視角，開發教學設計，在真實的教學情境中實踐教學設計。研究梳理了數學教育領域的相關理論，從學生認知、思想方法和數學史3個維度來設計課堂教學，并總結出數學史融入數學教學的一般流程。

關鍵詞：HPM? 反證法? 教學設計

中圖分類號：G642 ? ?文獻標識碼：A 文章編號：1672-3791（2019）11（b）-0120-03

近幾年，關于HPM的研究發展迅速，HPM的文章也是層出不窮，但文章的涉及面很多是中小學。基于已有的研究出發，能夠以HPM的視角對反證法進行教學，采用設計研究的方法，解決反證法教與學的問題，并以此更深一步研究，主要圍繞以下問題展開。

（1）學生理解反證法是否呈現出歷史相似性，歷史相似性研究是HPM領域研究中的一個方向，也是HPM研究者進行數學史融入數學教學的理論基礎。

（2）HPM視角下反證法教學對學生對數學概念、定義的理解以及對學生的情感態度與價值觀有什么影響？從HPM視角下去實施教學，問題是此教學是否對學生有影響，能否解決教學中存在的問題。

（3）HPM視角下數學反證法教學對教師的專業發展有什么影響？可以從教師對HPM教學知識、教學能力、教學信念來考察參與HPM視角下數學反證法教學過程中的專業發展，此問題可以分解為：①HPM視角下數學反證法教學對教師的信念產生的影響;②HPM視角下數學反證法教學對教師知識產生的影響;③HPM視角下數學反證法對教師的教學能力產生的影響。

1? 數學反證法的歷史

數學的發展出現過3次危機，每一次都和一個悖論有關，而最終的解決又勢必推動數學的向前發展，取得重大的突破，產生劃時代的數學成就。

什么是悖論呢？從推理過程看上去合乎情理，但結果卻得出了矛盾。悖論在很多情況下表現得出不符合排中律的矛盾命題：由真，可以推出它為假;由假，則可以推出它為真。這種嚴格性大家公認為是數學的一個主要特點，因此如果數學中出現悖論則會造成對數學可靠性的懷疑。

第一次數學危機由希帕索斯悖論引發，這個悖論的產生和勾股定理有著密切的聯系，并且最終促成了無理數的發現，對以后的數學發展產生了深遠的影響，在解決這次危機的過程中，有許許多多的科學家為之付出了努力，有的甚至還付出了生命的代價。

數學第一次危機發生在公元前580～568年之間的古希臘，數學家、哲學家畢達哥拉斯創立了畢達哥拉斯學派，這個學派發現并且證明了勾股定理，畢達哥拉斯在完成這一定理證明后欣喜若狂，殺牛百只以示慶賀。因此，這一定理還又獲得了一個帶神秘色彩的稱號：“百牛定理”，所以在西方將勾股定理稱為畢達哥拉斯定理[3]。

“萬物皆數”是該學派的哲學基石，是畢達哥拉斯提出的著名命題“一切數均可表示成整數或整數之比”，因為整數可以看成是分母為1的分數，整數與整數的比就是分數，分數和有理數的等價性，整數或整數之比實際上就是有理數，畢達哥拉斯學派的數學信仰就是現在我們所熟悉“一切數都可以表示成分數”。畢達哥拉斯定理（勾股定理）提出后，希帕索斯（學派中的一個成員）發現了一個問題：一個邊長為1的正方形的對角線長度既不能用整數表示，也不能用分數表示，而只能用另外一個屬來表示，這個數就是，這就是希帕索斯悖論，也叫作畢達哥拉斯悖論。這個的出現在數學界掀起了一場風暴。它直接動搖了畢達哥拉斯學派的數學信仰，使畢達哥拉斯學派為之大為恐慌。

在當時直接導致了人們認識上的危機，畢達哥拉斯學派認為希帕索斯就是魔鬼的化身，這位天才的思想家被投進了大海，為科學獻身的第一人。但是希帕索斯的名字卻和一樣，讓后人永遠地記住了他，希帕索斯也成了有史以來第一個使用反證法的人。

設正方形的邊長為1，其對角線為a，那么根據畢達哥拉斯定理α2=2，假設a是分數，設（p，q既約），有，即，從而可得q是一個偶數，那么q也是一個偶數，再令q=2m，代到q2=2p2里面，4m2=2p2也就是4m2=p2，這樣就得到p2是一個偶數，那么p也一定是一個偶數，這和p，q既約是相矛盾的，從而可以得到a不能表示成分數，也就是說邊長為1的正方形的對角線不能用整數之比來表示。

這種現象并不是唯一的，而是普遍的，比方一邊長為1另一邊長為2的矩形的對角線也不能用整數之比來表示，這無異于在平靜的水面上投下了一塊巨石一般，在當時的數學上和認識上掀起了軒然大波，引起了認識上的恐慌。為了擺脫這種尷尬，許多學者開始致力于化解這一危機。從這次數學危機得出，僅憑直覺和經驗不一定正確，要經過推理證明才是可靠的。

2? 反證法教學設計與研究

反證法是逆向思維的典型方法，其獨特的思維方式對提高數學思想有著重要的意義。它不僅具有強大的論證威力，而且越是困難的問題它越有功效。要想深刻理解反證法，就要深刻地領悟“正難則反”的思維原理。通過證明反論題為假而間接證明原論題為真的方法，叫作反證法，反證法證明步驟。

（1）反設：假設命題的結論不成立，即假設結論的反面成立，這個假設叫作“反證假設”。

（2）歸謬：由反證假設出發，運用已知條件，進行正確推理，導致矛盾。

（3）肯定：由所得矛盾，斷定反證假設不成立，從而肯定結論成立。

其中第（2）步是關鍵，主要尋找以下矛盾：與反證假設相矛盾;與已知條件相矛盾;與已知事實、定義、公理、前此定理相矛盾;自相矛盾。

3? 反證法應用

當用直接證法無法下手甚至不可能時，可使用反證法。

反證法更適用于：否定性問題;唯一性問題;存在性問題;無限性問題;同一性問題（逆命題成立）;學科起始性定理;命題結論的反面中唯一，應用窮舉反證法。基于HPM反證法的教學設計需要考慮教學設計要解決教學問題，需要了解具體的數學內容的歷史，科學準確地理解其本質，在學生現有的認知基礎上，應用教學理論來完成教學設計。在教學設計中恰當地融入數學史，使得教學更加符合學生認知，學生更容易理解，更好地解決數學問題，提高學生學習興趣，增強學生學習自信心[1]。

3.1 教學設計的3個維度

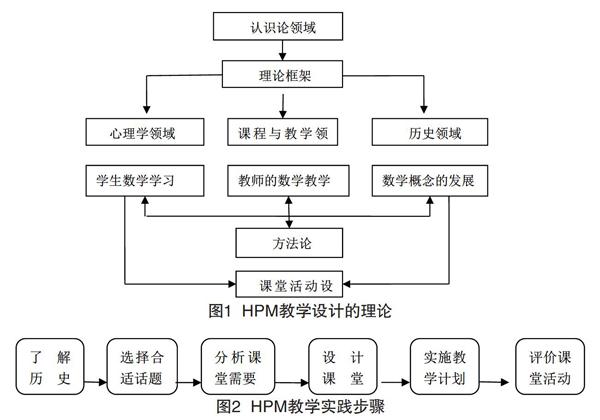
一個教學設計要考慮課程與教學論領域，同時還要注意課程標準、教學內容、教學方法，教師的數學教學觀等直接影響到教學（見圖1）。

如何設計HPM理論與實踐連接，把數學史融入到教學中，從而設計有效的教案;關鍵是促進教師專業發展，引領教師的HPM。通過建立HPM學術共同體把HPM領域教學實踐，從理論與實踐兩個方面解決上述問題（見圖2）。

3.2 教學設計的策略

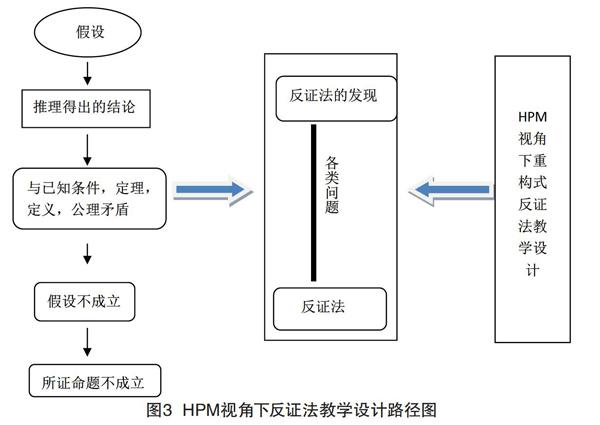
融入數學史的反證法教學，關鍵部分就是教學設計，如何設計HPM視角下的反證法教案呢，經過閱讀部分研究者的HPM的設計及反證法的教學有了設計思路（見圖3）。

根據以上HPM設計框架初步設計了反證法的教學設計，讓學生經歷數學反證法的演進過程，從中發現反證法的原理，以重構式來進行反證法概念教學，以系列趣味題來激起學習的興趣，在探索中學習歷史，發現數學。

4? 反證法研究的學生反饋及教學反思

（1）這種融入教學史的方式受到學生的喜歡，學生情感價值觀也得到提升，培養了學生探索創新的能力，但是學生的成績或理解水平沒有得到很大的提升，這也反映出1、2次的課程的HPM教學不可能改變學生的成績，只有通過長期的HPM教學實踐，才能改變學生的學習興趣，培養學生的學習模式。從對學生的反饋來看，仍有不少學生表示反證法不好理解，效果也沒有想象得好，實踐中還需繼續摸索。

（2）HPM視角下的反證法教學，僅僅教學研究的需要和嘗試，教師準備也比較費時，但也有利于教師的專業發展。首先，教師的教育信念有了變化，教師認識到讓學生理解定義及定理的重要，數學歷史讓教師感受到對學生認知的理解的重要性。其次，教師教學知識的增加了不少，在教學設計過程中，教師的數學史知識有所增加;教師了解教學設計的大體思路，如何設計更有利于達到教學效果。最后，教師的教學能力也得到提升，表現在教師開始有意識地關注與學生的互動，利用機會去激發學習動機，引導學生討論;同時，意識到在設計教學時，需關注學生的認知起點及認知過程的漸進性，知道選擇加工史料的方式方法，了解到如何從教育研究的角度幫助教學。

5? 研究的啟示

反證法教學設計要考慮學生的認識情況、對反證法的理解、對數學史的認識，建立數學的學習要與數學的歷史發展相聯系，有效地設計把數學史融入到課堂教學中去。通過研究述，構建了數學史融入數學課堂教學模式，總結出數學史融入數學課堂教學的一般實施流程。數學史融入數學課堂教學對老師要求更高，把數學史融入課堂教學需要老師將數學史的資料進行加工，使學生容易吸收真正達到優化課堂教學如何培養領域的教師專業化，如何促進教師應用來提升教學率。當前教師面臨著數學史知識缺乏、學生的升學壓力以及可直接應用的HPM視角下數學歸納法教學的設計研究案例缺乏等問題。解決這些問題的根本方法就是探索出領域的教師專業發展模式，以及詳細地分析教師專業發展的分析框架。

參考文獻

[1] 馮振舉，曲安京.HPM視野下的數學新課程內容構成[J].課程教材教法，2007，27（9）：38-42.

[2] 尹靜，王篤勤.教育設計研究與教師實踐性知識的構建[J].河北大學學報：哲學社會科學版，2013，38（2）：65-68.

[3] 李文林.數學史概論[M].3版.北京：高等教育出版社，2011.

[4] 周余峰.一次公開課的啟示——談新課程理念下的教學觀[J].數學教學通訊：中等教育，2013（24）：27-28.

[5] 陳惠勇.數學史觀下的數學概念教學新模式[J].高等數學研究，2007，10（5）：58-62.

[6] 沈衛國.康托對角線法中的邏輯問題及由此引出的反證法使用中必須注意的推理誤區[J].前沿科學，2017，11（2）：42-50.