數形結合思想在小學教學中的實踐運用
郝杰
摘 要:在新課程教育背景下,除了要求小學生掌握基本知識以外還要提高專業技能。尤其在數學學科上,更強調學生數學邏輯思維的養成。其中“數形結合”思想普遍應用在小學數學教育中,它不僅能夠降低數學難度,讓學生對數學知識有更好的理解,還能提高課堂教學效率。主要就“數形結合”思想在小學數學教學中的實踐運用進行探討。
關鍵詞:數形結合;小學數學;教學形式
一、“數形結合”思想的含義
“數形結合”思想是數學科目學習中的一種很重要的思想。它是指在研究相關數學問題時,根據數據想象圖形、根據圖形想象數據、將數與形相結合來思考問題的方法[1]。“數形結合”思想在小學數學教學中的實踐運用簡化了數學難度,使數學知識更直觀化地呈現出來,增強了小學生對數學的感性認知,有助于數學能力的提升。
二、“數形結合”思想下的教學形式
(一)從“數”到“形”轉化
從“數”到“形”的轉化適合代數知識在問題解決中的運用,主要是數與數之間的加減乘除。代數的學習要求學生有相應的邏輯能力和理解能力,但是小學生思想發育還不成熟,對于有些知識理解不到位,通過“幾何”轉化可以直觀地了解數量關系,從而增強學生對知識的理解。
(二)從“形”到“數”轉化
從“形”到“數”的轉化也就是在幾何學習中進行實踐運用,畢竟幾何問題對想象力有一定的要求,通過此種轉化可以將幾何思維轉化為數量關系,在一定程度上降低了學習難度。
三、數形結合思想在小學數學教學中的實踐運用
(一)利用數形結合思想培養小學生興趣
“數形結合”教育思想不但簡化了數學學習的難度,還豐富了教學形式,吸引了學生的注意力,使學生在好奇心的驅使下探究學習,全面理解教材內容,從而增加學生在數學學習上的信心,提高學習興趣。例如在學習“6~10的認識和加減法”時,為了使學生對5以上位數的加減法有更深的認識,教師可以采用“數”變“形”的教學方式,將6~10之間的數字通過圖形表示出來,從而增強學生對數字運算的感性認知。如9-5的運算,教師可以在多媒體上展示九朵花,其中五朵為玫瑰花,剩余四朵為月季花,引導學生9-5相當于在九朵花中拿掉五朵玫瑰花,剩下的月季花數就是該運算的答案。再比如對六年級下冊“負數”的學習中,小學生很難分清楚什么是正數什么是負數,教師就可以將正負數用數軸表示,為了增加講述過程中的趣味性,在0處畫一棵大樹,小麗向大樹左邊走了4 m,小紅向大樹右邊走了2 m,左邊表示正方向,右邊就是反方向,那么小麗行走的距離和方向表示為“4”,小紅行走的距離和方向表示為“-2”。以此種方式培養學生數學學習興趣,提高教學質量。
(二)利用數形結合思想提高數學理解能力
數學學習存在抽象性,尤其是在幾何學習中,不但是教師教學中的難點,也是學生在學習過程中最頭疼的部分,由于幾何知識對空間想象力要求比較高,小學生的思想發育程度難以滿足復雜知識點的要求,往往在幾何學習中遇到阻礙,理解不夠透徹。因此,教師可以將“形”轉換為“數”降低難度,幫助學生理解。例如,在“角的初步認識”教學中,為了讓學生學會對角進行區分和判斷,讓學生利用量角器測量直角的角度、鈍角的角度以及銳角的角度,從而將90°、大于90°、小于90°的概念與直角、鈍角、銳角概念進行聯系,加深小學生對角的認識。
(三)利用數形結合思想提高問題解決能力
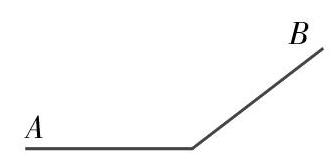
數學學習的目的是運用數學知識解決問題,其中數形結合思想可以為學生提供解題思路和方法。但是在此過程中還需要教師正確合理的引導,培養學生解決問題中善于將數量關系轉化為圖形,又或者將圖形轉化為數量關系,使“數形結合”思想牢固在學生心中。例如小學常見題型:汽車從A地出發到B地,先平地行駛,再上坡,其中平地上行駛速度為15 km/h,行駛了2 h,上坡行駛速度為10 km/h,行駛了4 h,汽車下坡速度為20 km/h,那么汽車從B地到A地用了多長時間?如果直接讓小學生進行解答,題中一大堆數據容易給學生造成困難,在思路上不能夠清晰梳理,如果將“數形結合”思想引用到解題思路中,教師就可以引導學生將路線圖畫出來,然后根據圖形掌握路徑情況,從而了解問題中存在的數量關系,再結合數學公式解決問題。
由此可知,小學數學教學需要不斷探究,將“數形結合”思想運用到數學教學活動中,善于在“數”“形”之間的互相轉變,不斷提高學生學習興趣,對數學問題的解決能力,在實踐活動中體會該思想的應用價值,從而將其內化于心,在潛移默化中變為一種解決問題的思想,提高小學生數學綜合能力。
參考文獻:
[1]周仁倫.數形結合思想在小學數學教學中的實踐運用[J].文理導航(下旬),2018(4):27-28.
[2]宋成文.基于“數形結合”思想的小學數學高效教學課堂的構建[J].中華少年,2018(4):164.

