同域重組，“玩”轉數學

裘永福

[摘? 要] 在核心素養深入踐行的當下課堂中，我們的復習課不能沒有核心素養的價值引領，不能僅僅為了復習而復習，也不能僅為了教學而教學. 此時，“同域重組”這一教育教學新名詞可以為我們的數學復習課堂開啟新航標. 文章談談同域重組教學在初三數學復習教學中的應用，談談核心素養的滲透策略.

[關鍵詞] 同域重組;初三數學;復習課;核心素養

“同域重組”是近幾年教學科研中的一個新名詞，就是將同一門學科甚至不同學科間相關聯的知識內容串聯成一個板塊或框架進行教學的一種方式. 狹義地來講，就是將現有的學材進行再加工，重新構建成新學材的過程. 經過實踐，筆者認為該種教學方式在初三數學復習課的教學中有著積極的作用，下面結合教學過程中的實例簡要談談筆者的幾點見解.

制定復習計劃是初三數學復習實施的第一步，也是極其重要的一步，它是勾勒即將開展的復習課“圖紙”的過程，“良好的開端等于成功的一半”，合理的復習計劃是確保復習課高效實施的重要條件. 照本宣科式的復習計劃雖可以取得一定的成效，但效果不佳，在重視創造力培養的當下，“炒冷飯”式的復習已不再適合新時代的學生. “同域重組”是教師針對所授班級的學生特點進行學材再建構的過程，具有一定的針對性和個性化，利于復習計劃的制定及復習中的時間支配.

函數部分是初中數學的重點和難點，通常使很多學生望而生畏，也使教師覺得在復習中難以把控，反復強調后學生依舊不理解是教師在復習函數時普遍的感受. 不難發現，函數部分的難點不在于單純的函數問題，而在于函數知識與其他知識的融合，這便是同域知識，因此教師在復習函數時要將函數與其他板塊知識的融合作為復習的重點. 如在一輪復習時將現有學材進行重組，將平面直角坐標系、方程（組）、不等式（組）、一次函數、二次函數、反比例函數、函數的應用進行整合，強調同域知識間的融合. 這樣可以更好地支配復習的時間，有針對性地進行復習，提高復習的效率.

將同域知識進行重組而不按考綱進行復習聽起來有點荒誕，但其實質是通過對學材及學生的分析，取其精華，省去重復的無用功，使得其實用性更強的復習方式. 這種復習真正實現了以學定教、以教促學，將復習與生長、知識與技能、思想與方法悄然無息地融合在復習的活動中，學生生長的不僅僅是數學思想與方法，還有數學學科特有的學科素養.

掌握

學習的過程就是知識建構的過程，學生知識建構的效果是復習效果的重要衡量指標. 復習課是穩固基礎、提高能力的過程，讓學生感知知識間的內在聯系與系統性是復習的重要目標，同域知識的重組可以在這一方面起到積極的作用.

統計與概率的內容難度不大，是中考數學的易得分點，因此將這兩部分內容整合后即可縮短復習時間. 利用上述知識導圖可以讓學生體會到概率與統計之間的聯系，感知到描述與分析數據的方法. 在復習過程中，再加之少而精且具有代表性的問題即可取得復習成效，讓學生系統掌握該部分的知識. 而且在這個復習的過程中，學生的站位和視角都會發生改變，這種站位和視角才是我們中考復習所需要的，也是學生能力提升的關鍵切口所在.

提高學生的數學能力也是復習的重要目標，誠然，人的各方面能力都是從鍛煉中積累起來的. 片面地說，復習是為了提高學生的解題能力，而在這個過程中，綜合問題是最好的學習與練習資源，在對同域知識的挖掘與重組中，開發綜合問題是提高學生的數學整體能力、讓學生學會融會貫通的有效方法.

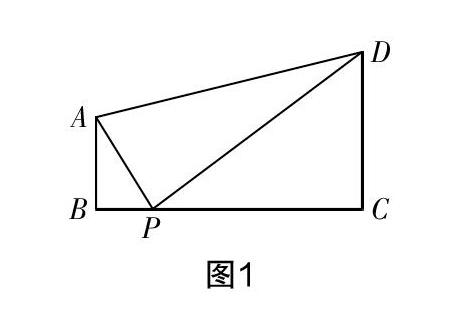
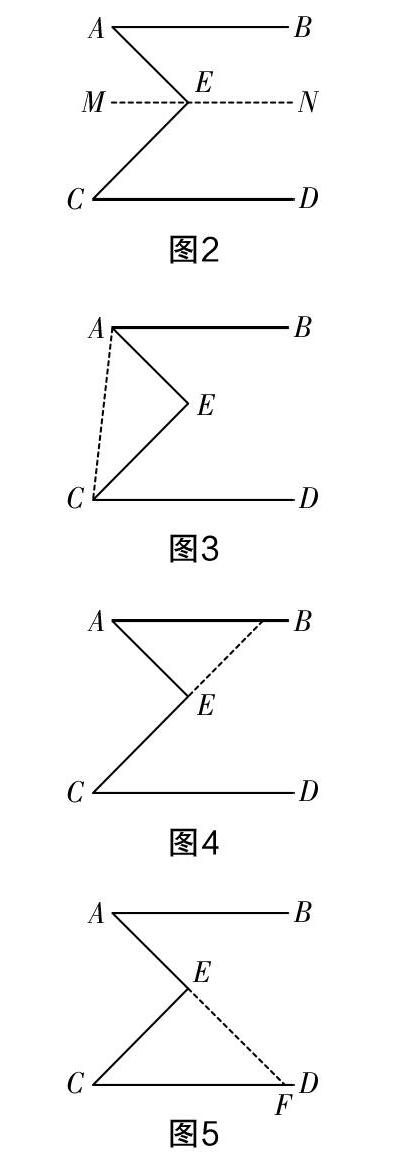
如在復習課“圖形的相似”中，下面是一個常用的例題：

上述問題是典型的“一線三等角”問題，主要是利用三角形相似得出相關結論. 顯然，與圖形有關的同域知識有很多，包括全等三角形、多邊形、圓的有關問題、路徑最短問題等. 因此我們可以針對圖3對問題進行開發.

問題1：在點D變化的過程中，AE的長度是否存在最小值？如果存在，求出此時BD的長度.

問題2：如果以A為圓心，以AE為半徑的圓與BC相切，此時BD的長度為多少？

問題3：當△ADE為等腰三角形時，求對應的BD的長度.

上述三個問題中，問題1為長度的最值問題，利用函數思想，設BD=x，AE=y，將y表示成關于x的二次函數，利用函數的最值解決問題;問題2為三角形與圓結合的問題，過點A作BC的垂線，垂線段的長度即和AE相等，再結合BA·CE=BD·CD列出方程求解;問題3為三角形問題，需要分三種情況來求解.

由上述問題可以看出，我們在復習時的內容并不是單一的，一個知識板塊下可以衍生出其余的知識，這便是同域知識的存在. 通過對同域知識的挖掘，可以讓問題的容量無限擴大，學生的思維能力也能得到發散，學會在數學中將前后知識融會貫通，從而得到整體的提高.

“教育如果沒有情感，就沒有愛，就像池塘沒有水一樣”，數學情感也是數學學習的重要部分，在教育中如果忽視了情感的培養，則學生往往思維能力不強. 數學情感指的是在數學活動中，通過一系列的探索與實踐，學生對數學產生的強烈求知欲與好奇心，感受數學學習的過程，體會數學的價值，對數學產生積極的肯定及愉快的情感體驗. 而興趣是最好的老師，只有將知識和情感有意結合起來，才能將學生的潛能激發出來，培養他們的創造能力.

引入環節是課堂教學的“開場舞”，該環節的效果很大程度上決定了學生對該堂課教學內容的興趣. 不管是新授課還是復習課，引入環節同等重要. 如三角形的有關內容是初中數學的重要內容，其中包括三角形、全等三角形、相似三角形，它們屬于同域內容. 在同域知識重組復習時，如何恰到好處地設置引入環節是我們需要斟酌的. 下面以同域重組復習課“三角形的那些事”為例，談談引入過程.

師：三角形是我們初中數學中的“大腕”，大家知道它有多重要嗎？

生1：考得比較多、分數占比較大.

師：沒錯，這位同學的憂患意識比較強，隨時都將考分放在重要的位置. 能不能具體說明呢？

生2：一個三角形我們需要掌握它的邊、角、三條重要線段，兩個三角形需要掌握全等和相似.

師：你想到了多個方面，思維很開闊，其他同學還有要補充的嗎？

生3：一個三角形中還有特殊三角形的性質及判定.

生4：還有三角形的外角.

生5：銳角三角函數也是與三角形有關的內容.

……

師：大家表現都很棒，集體的智慧真是無限的，剛才同學們已經將與三角形有關的知識基本上全部羅列出來了，接下來我們就一起用問題來仔細說說三角形的那些事兒.

上述環節既是引入，也是對知識的回顧，通過這種方式的提問，讓學生回顧了與三角形有關的基礎內容，留在學生腦海中的知識點雖然有些零散，但相互補充之后已經很全面了，在這個基礎上教師再呈現系統的知識導圖，其效果明顯優于教師直接進行知識點的灌輸. 用這種方式，可以引起學生對數學的興趣，簡單的提問可以讓學生體會到成功的喜悅，思考問題的魅力，也可以讓學生對同域重組的知識有系統的認識，誘發學生的數學情感.

同域重組復習是一種“不走尋常路”的復習方式，是一種有針對性的個性化教學，教師可以隨時根據所教授班級學生的實際情況對教學內容進行調整，以適應學生的變化. 它建立在教師對學材再開發的基礎上，因此，對于教師而言，提高個人基本功及數學素養是非常重要的，只有教師對學材不斷探索、對問題不斷開發，才能引領學生“玩”轉數學，真正凸顯同域重組的價值，引領學生核心素養的漸進提升.