2018年中考數學文化型試題背景賞析

余小芬 閔蓉 劉成龍

[摘? 要] 文章分析了2018年中考數學文化型試題的六類命題背景：以“算經十書”為背景，以《數書九章》為背景，以《算法統宗》為背景，以“勾股定理”證明為背景，以“割圓術”為背景，以“楊輝三角”為背景.

[關鍵詞] 中考數學;試題背景;數學文化;賞析

數學是人類文化的重要組成部分，數學課程應適當反映數學的歷史、應用和發展趨勢……數學科學的思想體系、數學的美育價值、數學家的創新精神、數學課程應幫助學生了解數學在人類文明發展中的作用，逐步形成正確的數學觀. 所謂數學文化，從狹義上講是指數學的思想、精神、方法、觀點、語言，以及它們的形成和發展;從廣義上講就是除上述內涵以外，還包含數學家、數學史、數學美、數學教育、數學發展中的人文成分、數學與社會的聯系、數學與各種文化的關系等等. 2011年版《義務教育數學課程標準》指出：“數學文化作為教材的組成部分，應滲透在整套教材中.為此，教材可適時地介紹有關背景知識，包括數學在自然與社會中的應用，以及數學發展史的有關材料，幫助學生了解在人類文明發展中數學的作用，激發學習數學的興趣，感受數學家治學的嚴謹，欣賞數學的優美. ”因此，在各版本的初中數學教材中，涌現了一大批與數學文化有關的閱讀材料或例題、習題，例如“方程”史話、楊輝三角、漫畫勾股世界、海倫——秦九韶公式、投針實驗等等. 這些內容的設置，不僅有利于弘揚博大精深的數學文化，還能激發學生的數學學習興趣，開拓學生視野，幫助學生理解數學、熱愛數學，從而不斷提升他們的數學核心素養. 近年來，以數學文化作為試題背景已成為中考命題的新亮點、新趨勢. 例如2015年湖南常德中考以“角谷猜想”為背景考查代數式的運算，2016年孝感中考以“趙爽弦圖” 為背景考查正方形性質、正切三角函數定義，2016年鹽城中考以“費馬點”為背景考查線段長度最值問題等. 2018年，各地中考堅持“立德樹人”“文化育人”的基本理念，命制了一批背景豐富的數學文化試題，本文對這些優秀試題的命題背景進行賞析，以饗讀者.

以“算經十書”為背景

“算經十書”是中國傳統數學的經典. 所謂“算經十書”，指的是中國十部古算書：《周髀算經》《九章算術》《孫子算經》《五曹算經》《夏侯陽算經》《張丘建算經》《海島算經》《五經算術》《緝古算經》《綴術》（元豐年間已失傳，后來以《數術記遺》代之）. 唐代國子監內設算學館，置有博士、助教，指導學生學習數學，規定這十部書作為課本. “算經十書”分別總結了當時的數學成就，對數學的發展起到了巨大的推動作用，構成了具有中華民族自身特色的傳統數學體系.

例1? （2018年江西中考第9題）中國的《九章算術》是世界現代數學的兩大源泉之一，其中有一問題：“今有牛五、羊二，直金十兩. 牛二、羊五，直金八兩. 問牛羊各直金幾何？”譯文：今有牛5頭，羊2頭，共值金10兩;牛2頭，羊5頭，共值金8兩. 問牛、羊每頭各值金多少？設牛、羊每頭各值金x兩、y兩，依題意，可列出方程組為__________.

評析? 《九章算術》是中國古代第一部數學專著，是“算經十書”中最重要的一種. 該書內容十分豐富，全書采用問題集的形式，收集246個與生產、生活實踐有聯系的應用問題，系統總結了戰國、秦、漢時期的數學成就. 同時，《九章算術》在數學上還有其獨到的成就，不僅最早提到分數問題，也首先記錄了盈不足等問題. “方程”這章還在世界數學史上首次闡述了負數及其加減運算法則. 《九章算術》是一本綜合性的歷史著作，是當時世界上最先進的應用數學，它的出現標志中國古代數學形成了完整的體系. “方程”是《九章算術》的第八章，“方程”指的是一次方程組，而一次方程組又是利用算籌（算籌表示未知數的系數及相應的常數項）布置而成的，其形狀有如方陣，故稱之為方程. 我國古代數學家劉徽在《九章算術注》指出：“程，課程也. 二物者二程，三物者三程，皆如物數程之，并列為行，故謂之方程.” 本題根據“牛的單價×牛的數量+羊的單價×羊的數量=總價”，不難得到方程組為5x+2y=10，

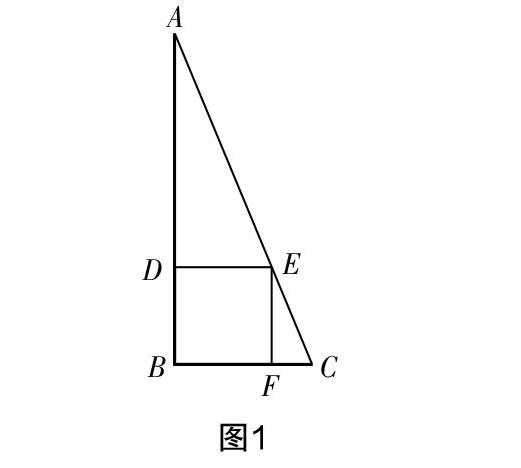
例2? （2018年岳陽中考第15題）《九章算術》是我國古代數學名著，書中有下列問題：“今有勾5步，股12步，問勾中容方幾何？”其意思為：“今有直角三角形，勾（短直角邊）長為5步，股（長直角邊）長為12步，問該直角三角形能容納的正方形的邊長最大是多少步？”

評析? “勾股”是《九章算術》的第九章，主要介紹利用勾股定理求解各種問題. 本題以《九章算術》中幾何問題為背景，考查對勾股定理的應用及求解直角三角形的最大內接正方形. 如圖1，設在Rt△ABC中，能容納的最大正方形DEFB的邊長為x，由相似不難得到=，即=，解得正方形邊長x=.

特別指出，2018年全國各地中考中，以《九章算術》為背景考查列（或解）一次方程組的試題較多，比如2018年湖北襄陽中考第13題、2018年河南中考第6題、2018年廣州中考第8題、2018年湖北宜昌中考第19題等.

例3? （2018年安徽中考第16題）《孫子算經》中有這樣一道題，原文如下：今有百鹿入城，家取一鹿，不盡，又三家共一鹿，適盡. 問：城中家幾何？大意為：今有100頭鹿進城，每家取一頭鹿，沒有取完，剩下的鹿每3家共取一頭，恰好取完. 問：城中有多少戶人家？請解答上述問題.

評析? 《孫子算經》作者及成書年代不詳，傳本的《孫子算經》共三卷，上卷、中卷系統敘述了算籌記數法和籌算的乘、除、開方及分數等計算的步驟及法則，以及簡單的面積、體積的計算問題. 下卷是各種應用問題，其中著名的“物不知其數”：“今有物不知其數，三三數之余二，五五數之余三，七七數之余二，問物幾何？”舉世聞名，被譽為“中國剩余定理”或“孫子定理”. 還比如經典問題“雞兔同籠”： “今有雉兔同籠，上有三十五頭，下有九十四足，問雉兔各幾何？”更是古今中外“雞兔同籠”問題的始祖.

本題以《孫子算經》中分鹿問題為背景，考查學生對一元一次方程的理解. 由題意，可設城中有x戶人家，于是有x+=100，從而解得城中有75戶人家.

以《數書九章》為背景

《數書九章》又被稱作《數學大略》《數學九章》，其作者是我國南宋著名的數學家秦九韶（1202—1261年）. 《數書九章》全書九章十八卷，九章九類：大衍類、天時類、田域類、測望類、賦役類、錢谷類、營建類、軍族類、市物類，每類9題，共81題. 該書內容豐富至極，上至天文、星象、歷律、下至河道、水利、建筑、運輸，包括各種幾何圖形和體積，錢谷、賦役、市場、牙厘的計算和互易. 《數書九章》在一次同余式組解法和高次方程數值解法等方面取得了具有世界意義的光輝成就，我國數學史家梁宗巨對其這樣評價：“《數學九章》是一部劃時代的巨著，內容豐富，精湛絕倫. ”秦九韶也被美國著名科學史家薩頓譽為是“他那個名族，他那個時代，并且確實也是各個時代最偉大的數學家之一”.

例4? （2018年長沙中考第11題）我國南宋著名數學家秦九韶的著作《數書九章》里記載有這樣一道題目：“問有沙田一塊，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知為田幾何？”這道題講的是：有一塊三角形沙田，三條邊長分別為5里，12里，13里，問這塊沙田面積有多大？題目中的“里”是我國市制長度單位，1里=500 m，則該沙田的面積為（? ? ）

A. 7.5 km2 ? ? ? ? B. 15 km2

C. 75 km2 ? ? ? ? ?D. 750 km2

評析? 本題以《數書九章》中問題為背景，考查對勾股定理的應用. 根據題目中數據，不難得到52+122=132，故這個三角形是直角三角形. 再根據單位換算得：5里=2.5 km，12里=6 km，故該沙田的面積為×2.5×6=7.5 km2.

以《算法統宗》為背景

《算法統宗》是明代數學家程大位所著，它是一部以珠算為主要計算工具的應用數學著作. 全書共收集了595個問題，并穿插有大量的圖形和詩詞形式的歌訣. 梁宗巨先生指出：“明代在西方數學輸入之前，最大的成就可以說是珠算的發明，最重要的數學書要算程大位的《算法統宗》. ”

例5? （2018年邵陽中考第10題）程大位是我國明朝商人，珠算發明家. 他60歲時完成的《直指算法統宗》是東方古代數學名著，詳述了傳統的珠算規則，確立了算盤用法. 書中有如下問題：“一百饅頭一百僧，大僧三個更無爭，小僧三人分一個，大小和尚得幾丁. ”意思是：有100個和尚分100個饅頭，如果大和尚1人分3個，小和尚3人分1個，正好分完，問大、小和尚各有多少人？下列求解結果正確的是（? ? ）

A. 大和尚25人，小和尚75人

B. 大和尚75人，小和尚25人

C. 大和尚50人，小和尚50人

D. 大、小和尚各100人

評析? 本題以經典問題“百僧分百饅”為背景，考查二元一次方程組及其解法. 由題意，設大和尚有x人，小和尚y人，不難得x+y=100，

3x+=100， 故解得大和尚25人，小和尚75人.

2018年取材于《算法統宗》的中考試題還有福建中考第8題、浙江紹興中考第12題等.

以“勾股定理”證明為背景

例6? （2018年成都中考第22題）漢代數學家趙爽在注解《周髀算經》時給出的“趙爽弦圖”是我國古代數學的瑰寶. 如圖2所示的弦圖中四個直角三角形都是全等的，它們的兩直角邊之比均為2 ∶ 3. 現隨機向該圖形內擲一枚小針，則針尖落在陰影區域的概率為_________.

評析? 《周髀算經》是流傳到現在的一部最早的數學著作，同時也是一部“蓋天說”（中國古代的一種宇宙觀，認為天像一個斗笠，大地像一個翻扣的盆）的天文學著作. 《周髀算經》約成書于公元前100年，全書共二卷，內容是一些天文歷法及有關的數學問題，所包含的數學內容有分數計算、等差數列、勾股定理和測量等. 特別是關于勾股定理的論述，比畢達哥拉斯要早六百多年. 從古至今，《周髀算經》可以說是最純粹的中國國粹之一. 據史書記載，《周髀算經》并未直接給出勾股定理的證明方法，而是漢代數學家趙爽利用弦圖對此進行了證明. 弦圖精妙地展現了幾何圖形的截、割、拼、補，其構思精巧，富有創意，既表達著邏輯的嚴謹，又呈現了幾何的直觀，是數形結合的典范. 本題以趙爽弦圖為載體，考查勾股定理和幾何概型.

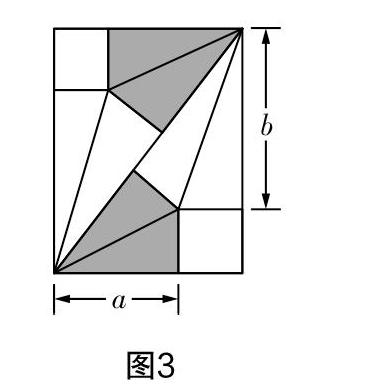
例7? （2018年溫州中考第10題）我國古代偉大的數學家劉徽將勾股形（古人稱直角三角形為勾股形）分割成一個正方形和兩個全等的直角三角形，得到一個恒等式，后人借助這種分割方法所得到的圖形證明勾股定理. 如圖3所示的矩形由兩個這樣的圖形拼成，若a=3，b=4，則該矩形的面積為（? ? ）

A. 20 ? ? B. 24C. D.

評析? 本題以數學家劉徽對勾股定理的證明為背景，讓學生從另一角度欣賞了圖形的割補技巧，感受我國數學文化的博大精深，感悟古代數學家的智慧和才能. 問題解決的關鍵是計算出小正方形的邊長，圖5的矩形由兩個直角三角形構成，每個直角三角形的邊長均滿足勾股定理：（x+3）2+（x+4）2=（3+4）2，其中x為小正方形的邊長，由此解出x，得到矩形的面積為（x+3）（x+4）.

以“割圓術”為背景

魏晉時期的數學家劉徽首創割圓術，為計算圓周率建立了嚴密的理論和完善的算法. “割圓術”是以圓內接正多邊形的面積來無限逼近圓面積，即“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體而無所失矣. ”“割圓術”通過無限分割的方式，體現了有限到無限、以直代曲的極限思想.

例8? （2018年宜賓中考第13題）劉徽是中國古代卓越的數學家之一，他在《九章算術》中提出了“割圓術”，即用內接或外切正多邊形逐步逼近圓來近似計算圓的面積. 設☉O的半徑為1，若用外切正六邊形來近似估計☉O的面積，則S=______（結果保留根號）.

評析劉徽用割圓術證明“半周半徑相乘得積步”的圓面積公式時，正是從內接正六邊形（“六觚”）開始割圓，依次得到內接正十二邊形（“十二觚”）、正二十四邊形（“二十四觚”）……認為割圓到最后就得到一個和圓重合的正無窮多邊形. 本題就以“割圓術”的最簡單情形（正六邊形）為背景，考查多邊形的內角和、銳角三角函數、勾股定理、三角形面積等基礎知識. 如圖4，由ABCDEF為正六邊形得△ABO為等邊三角形，又☉O的半徑為1，故OG=1，BG=AG=，因此AB=，所以S=6S=6×××1=2.

以“楊輝三角”為背景

“楊輝三角”是我國宋朝數學家楊輝于1261年在其所著《詳解九章算法》一書中提出的，歐洲人將楊輝三角稱為“帕斯卡三角”（于1654年由法國人帕斯卡發現）. 由此可見，我國比歐洲至少要早三百年發現這一偉大成果. “楊輝三角”結構對稱優美，蘊含豐富的規律和結論，古往今來、古今中外，吸引著無數數學愛好者去認識它、研究它. 同時，它也是現行高中教材中二項式定理中的重要內容，是中考、高考命題的良好素材.

例9? （2018年宜昌中考第8題）1261年，我國南宋數學家楊輝用圖5中的三角形解釋二項和的乘方規律，比歐洲的相同發現要早三百多年，我們把這個三角形稱為“楊輝三角形”. 請觀察圖中的數字排列規律，則a，b，c的值分別為（? ? ）

評析? 本題以“楊輝三角”為背景，考查學生的觀察能力，不難發現“楊輝三角形”左右兩邊上的數都是1，其余的數為它肩上的兩數之和，故a=1+5=6，b=5+10=15，c=10+10=20.

總之，中考試題中滲透數學文化，不僅弘揚了古今中外數學所取得的卓越成就，推廣了數學經典著作，而且幫助學生開闊了眼界、增長了知識、啟迪了心智.

基金項目：四川省“西部卓越中學數學教師協同培養計劃”項目（ZY16001）.

作者簡介：余小芬（1986-），四川內江人，碩士，講師，主要研究方向：數學教育及中高考研究;閔蓉（1999-），四川眉山人，內江師范學院數信學院數學與應用數學專業2017級3班學生;劉成龍（1985-），四川內江人，碩士，講師，主要研究方向：數學教育及中高考研究.