中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化的政策仿真與模擬
張樨樨 劉鵬

摘要:在中國(guó)海洋漁業(yè)產(chǎn)業(yè)面臨資源枯竭、投產(chǎn)失衡、負(fù)生態(tài)效應(yīng)背景之下,海洋牧場(chǎng)生態(tài)系統(tǒng)成為支撐藍(lán)色糧倉(cāng)戰(zhàn)略、促進(jìn)海洋經(jīng)濟(jì)發(fā)展、改善海域生態(tài)不可或缺的重要實(shí)體。激發(fā)海洋牧場(chǎng)政策內(nèi)驅(qū)力,挖掘海洋牧場(chǎng)發(fā)展?jié)摿Γ苿?dòng)漁業(yè)產(chǎn)業(yè)新舊功能轉(zhuǎn)換及轉(zhuǎn)型升級(jí)是促進(jìn)中國(guó)海洋經(jīng)濟(jì)內(nèi)涵式發(fā)展的核心要義之一。科學(xué)確定海洋牧場(chǎng)生態(tài)系統(tǒng)的各子系統(tǒng)構(gòu)成及評(píng)價(jià)指標(biāo),構(gòu)建系統(tǒng)動(dòng)力學(xué)模型解析生態(tài)系統(tǒng)多變量間雜糅關(guān)系;選取政策調(diào)節(jié)變量對(duì)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化的政策組合進(jìn)行5種模式仿真,嘗試模擬2017—2035年不同政策模式下中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)發(fā)展趨勢(shì)。由對(duì)比分析可知:10個(gè)牧場(chǎng)區(qū)在海洋科研投入、水產(chǎn)技術(shù)推廣人員與機(jī)構(gòu)構(gòu)成方面存在顯著差異;海洋牧場(chǎng)生態(tài)系統(tǒng)的良性發(fā)展依賴海洋科研與環(huán)境投入,環(huán)境保護(hù)與提升的不間斷投入需持續(xù)增強(qiáng);海洋科研投入以技術(shù)升級(jí)為媒介提升牧場(chǎng)環(huán)境質(zhì)量,但水產(chǎn)技術(shù)推廣的投入產(chǎn)出效率較低,應(yīng)重點(diǎn)關(guān)注水產(chǎn)技術(shù)推廣人員隊(duì)伍建設(shè)與再培訓(xùn)。發(fā)揮科技與環(huán)境政策協(xié)同效應(yīng)是提升政策績(jī)效的關(guān)鍵,健全完善“政企學(xué)研”多元融合投入機(jī)制,加快水產(chǎn)技術(shù)推廣工作,改革向常態(tài)化、專業(yè)化、信息化轉(zhuǎn)變,以域外經(jīng)驗(yàn)借鑒為契機(jī)打造水產(chǎn)技術(shù)推廣人才培養(yǎng)特色化體系,打磨政策適配與銜接細(xì)節(jié),形成海洋牧場(chǎng)生態(tài)系統(tǒng)環(huán)境保護(hù)與科技創(chuàng)新協(xié)同發(fā)展的創(chuàng)新政策模式。
關(guān)鍵詞:海洋牧場(chǎng);生態(tài)系統(tǒng);系統(tǒng)動(dòng)力學(xué);政策仿真;系統(tǒng)模擬
中圖分類號(hào):F205 文獻(xiàn)標(biāo)識(shí)碼:A 文章編:號(hào)1002-2104(2019)12-0168-09 DOI:10.12062/cpre.20190611
中國(guó)海疆遼闊,岸線綿長(zhǎng),擁有優(yōu)越的海洋生態(tài)條件與豐富的海水資源。受人口增長(zhǎng)、工業(yè)污染、長(zhǎng)期粗放式發(fā)展等諸多因素的影響,海洋生態(tài)環(huán)境逐漸惡化,資源嚴(yán)重衰退,中國(guó)海洋經(jīng)濟(jì)的長(zhǎng)期良性可持續(xù)發(fā)展受到嚴(yán)重威脅。海洋漁業(yè)的投產(chǎn)不均、過(guò)度開(kāi)發(fā)導(dǎo)致海洋漁業(yè)資源加速枯竭的同時(shí)[1],破壞了海洋生態(tài)經(jīng)濟(jì)系統(tǒng)平衡。海洋牧場(chǎng)作為促進(jìn)海洋經(jīng)濟(jì)綠色發(fā)展、加快傳統(tǒng)海洋漁業(yè)轉(zhuǎn)型的可持續(xù)發(fā)展性強(qiáng)、綜合效益高的新模式,不僅能夠涵養(yǎng)海洋資源,提升經(jīng)濟(jì)效益,而且優(yōu)化海域環(huán)境,促進(jìn)多產(chǎn)業(yè)融合,已成為中國(guó)海洋經(jīng)濟(jì)生態(tài)系統(tǒng)良性發(fā)展的重要引擎。
中國(guó)海洋牧場(chǎng)建設(shè)與發(fā)展時(shí)間較短,尚處在由漁業(yè)農(nóng)牧化向生態(tài)養(yǎng)殖、科普研發(fā)、休閑娛樂(lè)、觀光旅游等模塊集成綜合體過(guò)渡的發(fā)展階段,問(wèn)題集中涌現(xiàn)。2017年的《國(guó)家級(jí)海洋牧場(chǎng)示范區(qū)建設(shè)規(guī)劃(2017—2025)》提出,到2025年,在全國(guó)范圍內(nèi)建成178個(gè)具有輻射示范效應(yīng)的國(guó)家級(jí)海洋牧場(chǎng)。同時(shí)指出,雖然海洋牧場(chǎng)建設(shè)取得成績(jī),與海洋生態(tài)文明建設(shè)與漁業(yè)轉(zhuǎn)型升級(jí)要求還存在較大差距,支持政策體系有待完善、科技與環(huán)境支撐薄弱、固定資產(chǎn)投產(chǎn)比偏低、牧場(chǎng)建設(shè)系統(tǒng)化程度不高、配套技術(shù)推廣不到位等表征較為突出,問(wèn)題散亂且雜糅。以上種種問(wèn)題均可在海洋牧場(chǎng)生態(tài)圈系統(tǒng)的集成與優(yōu)化中找到病根,診治切不可“頭痛醫(yī)頭,腳痛醫(yī)腳”。鑒于此,本研究在模擬仿真中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)實(shí)景下進(jìn)行政策組合與效果評(píng)價(jià),在生態(tài)系統(tǒng)協(xié)同優(yōu)化演進(jìn)過(guò)程中,深入挖掘系統(tǒng)各要素運(yùn)行機(jī)制,科學(xué)確定適配政策的應(yīng)用時(shí)機(jī)與尺度。
1文獻(xiàn)述評(píng)
通過(guò)文獻(xiàn)聚合,梳理提煉與海洋牧場(chǎng)相關(guān)的研究焦點(diǎn)與熱點(diǎn),分為四個(gè)專題進(jìn)行文獻(xiàn)匯總與評(píng)析。
第一,從國(guó)家與地區(qū)層面研究海洋牧場(chǎng)的相關(guān)政策。韓楊通過(guò)分析建國(guó)以來(lái)中國(guó)海洋漁業(yè)配套政策提出,中國(guó)在投產(chǎn)控制、生態(tài)環(huán)境與監(jiān)管機(jī)制上存在一些問(wèn)題,導(dǎo)致了政策成效不理想[1]。通過(guò)梳理美國(guó)海洋漁業(yè)發(fā)展主要政策及與中國(guó)的對(duì)比發(fā)現(xiàn),中國(guó)海洋漁業(yè)管理在資源評(píng)估管理體系等方面與美國(guó)存在一定差距,應(yīng)從漁業(yè)管理計(jì)劃、資源份額管理等方面逐步加以完善[2]。Pablo Pita等[3]運(yùn)用EFLA框架分析英國(guó)、西班牙、葡萄牙等歐盟國(guó)家和歐洲的海洋漁業(yè)相關(guān)政策法規(guī),結(jié)果表明,歐洲在海洋漁業(yè)政策實(shí)施上嚴(yán)格遵循生態(tài)原則,發(fā)展可持續(xù)性逐步提升。Rob Southwick等[4]認(rèn)為,經(jīng)濟(jì)信息對(duì)海洋休閑漁業(yè)與海洋管理政策制定尤為重要,良好的經(jīng)濟(jì)反饋能夠提升公眾對(duì)產(chǎn)業(yè)的認(rèn)可度,有利于政策實(shí)行。
第二,從利益相關(guān)者視角探討海洋牧場(chǎng)政策擬定過(guò)程中的利益沖突問(wèn)題。Saba Siddiki[5]發(fā)現(xiàn),美國(guó)開(kāi)始通過(guò)構(gòu)建多維利益相關(guān)者團(tuán)隊(duì)進(jìn)行海洋牧業(yè)的政策研究與制定,該方法可以權(quán)衡包括政府組織和非政府組織的多方利益,在一定程度上能夠保證政策順利推行。Luke Fairbanks等[6]調(diào)查美國(guó)新英格蘭海水養(yǎng)殖業(yè)利益相關(guān)者對(duì)該行業(yè)的認(rèn)知發(fā)現(xiàn),各方利益相關(guān)者普遍認(rèn)為社會(huì)與政治因素對(duì)行業(yè)的影響不確定,很可能導(dǎo)致未來(lái)的利益沖突,建議政府建立區(qū)域性聯(lián)合機(jī)構(gòu)來(lái)推廣近海養(yǎng)殖與海域開(kāi)發(fā)。Luiz等[7]運(yùn)用GIS方法評(píng)估,由其他利益相關(guān)者綜合制定的巴西南部地區(qū)的海洋牧場(chǎng)選址政策方案,結(jié)果顯示存在較大風(fēng)險(xiǎn),各方專家與其他利益相關(guān)者對(duì)海洋牧場(chǎng)選址問(wèn)題考慮的方向有所不同:專家意見(jiàn)更為重視選址的生態(tài)環(huán)境標(biāo)準(zhǔn),而其他利益相關(guān)者更為注重物流問(wèn)題。Jinkai Yu等[8]闡述了中國(guó)海水養(yǎng)殖現(xiàn)狀及發(fā)展?jié)摿Γ赋鲞M(jìn)一步發(fā)展需要各方利益相關(guān)者的參與,建議設(shè)立海水養(yǎng)殖利益相關(guān)者管理部門,解決該產(chǎn)業(yè)轉(zhuǎn)型難、技術(shù)支撐不夠、風(fēng)險(xiǎn)較大等問(wèn)題。Lindland等[9]運(yùn)用扎根方法,探究挪威某沿海社區(qū)居民與其他利益相關(guān)者對(duì)海洋牧場(chǎng)發(fā)展的態(tài)度。研究表明,不同利益相關(guān)群體的潛在價(jià)值觀影響該態(tài)度,這些影響因素直接影響挪威沿海地區(qū)海洋漁業(yè)產(chǎn)業(yè)政策的制定。
第三,衡量海洋牧場(chǎng)、海水養(yǎng)殖的投入產(chǎn)出及關(guān)聯(lián)效應(yīng)。Eoin Grealis等[10]利用愛(ài)爾蘭水產(chǎn)養(yǎng)殖業(yè)投入產(chǎn)出數(shù)據(jù),通過(guò)里昂惕夫生產(chǎn)函數(shù)估計(jì)水產(chǎn)部門的相關(guān)乘數(shù),并將乘數(shù)用于分析可持續(xù)水產(chǎn)養(yǎng)殖業(yè)戰(zhàn)略目標(biāo)達(dá)成情況。結(jié)果表明,愛(ài)爾蘭水產(chǎn)養(yǎng)殖業(yè)不僅促進(jìn)了經(jīng)濟(jì)發(fā)展,增加了就業(yè),還顯著提升了經(jīng)濟(jì)發(fā)展的可持續(xù)性。Ma Dolores等[11]以西班牙加利西亞為例,通過(guò)均衡投入產(chǎn)出法分析了海水養(yǎng)殖對(duì)經(jīng)濟(jì)社會(huì)的影響。結(jié)果表明,海水養(yǎng)殖業(yè)發(fā)展能夠?yàn)樵摬块T創(chuàng)造收益,還可以提升其他部門收益。Jordi Guillen等[12]通過(guò)對(duì)歐盟海水牧場(chǎng)投入的描述性統(tǒng)計(jì)分析,結(jié)合投入政策梳理發(fā)現(xiàn),雖然在高投入下歐盟海洋牧場(chǎng)產(chǎn)出沒(méi)有顯著提升,但相關(guān)投入提升了海水養(yǎng)殖業(yè)的整體質(zhì)量和產(chǎn)品安全性,在保持生態(tài)友好發(fā)展模式的同時(shí),為消費(fèi)者帶來(lái)了品質(zhì)更高的產(chǎn)品。Lavanya等[13]通過(guò)構(gòu)建隨機(jī)超越對(duì)數(shù)函數(shù),分析紅樹(shù)林對(duì)印度海洋牧場(chǎng)的效用。結(jié)果顯示,紅樹(shù)林的涵養(yǎng)作用對(duì)海洋牧場(chǎng)產(chǎn)量的貢獻(xiàn)率較高。Holden等[14]以可持續(xù)發(fā)展視角考量加拿大不列顛哥倫比亞地區(qū)海洋漁業(yè)的社會(huì)經(jīng)濟(jì)效應(yīng)與生態(tài)效應(yīng)。通過(guò)對(duì)沿海養(yǎng)殖群體、原住民等主體的行為調(diào)查發(fā)現(xiàn),當(dāng)?shù)睾Q鬂O業(yè)產(chǎn)業(yè)在社會(huì)、經(jīng)濟(jì)、生態(tài)各層面存在較大發(fā)展?jié)摿Υ诰颍岢龅胤胶Q鬂O業(yè)發(fā)展應(yīng)與當(dāng)?shù)匾?guī)劃與政策適配。
第四,海洋牧場(chǎng)發(fā)展?jié)摿υu(píng)價(jià)及影響因素分析。Ian P. Davie等[15]依據(jù)國(guó)家綜合發(fā)展?jié)摿Α⒄咧贫ǖ纫蛩貙?duì)海洋牧場(chǎng)樣本進(jìn)行評(píng)估發(fā)現(xiàn),太平洋與加勒比海地區(qū)的政策管理有序,增長(zhǎng)潛力大;中國(guó)海洋牧場(chǎng)產(chǎn)出較高,但海域選擇存在一定生態(tài)問(wèn)題,私人資本介入影響了發(fā)展的可持續(xù)性。胡求光等[16]從資源、經(jīng)濟(jì)、環(huán)境、科技四個(gè)維度構(gòu)建海洋牧場(chǎng)發(fā)展?jié)摿υu(píng)價(jià)體系,對(duì)2007年和2011年中國(guó)海洋牧場(chǎng)區(qū)發(fā)展?jié)摿M(jìn)行橫縱向比較。結(jié)果表明,雖然海洋牧場(chǎng)區(qū)發(fā)展?jié)摿φw呈上升趨勢(shì),但支撐其發(fā)展的因素有所不同,區(qū)域內(nèi)部存在發(fā)展不平衡現(xiàn)象。梁鑠等[17]運(yùn)用隨機(jī)前沿分析等方法預(yù)測(cè)中國(guó)海水養(yǎng)殖生產(chǎn)潛力,中國(guó)海水養(yǎng)殖的空間及環(huán)境約束不大,但未進(jìn)行充分開(kāi)發(fā)。Johann Hofherr等[18]針對(duì)歐盟海水養(yǎng)殖產(chǎn)需不均衡問(wèn)題,探究海水養(yǎng)殖增長(zhǎng)速度緩慢的原因,發(fā)現(xiàn)歐盟并不存在海水養(yǎng)殖空間不足的問(wèn)題。進(jìn)一步研究發(fā)現(xiàn),局部空間的不同產(chǎn)業(yè)競(jìng)爭(zhēng)導(dǎo)致該問(wèn)題出現(xiàn),產(chǎn)業(yè)之間尚未形成相互促進(jìn)的協(xié)同效應(yīng)。Safford等[19]從科研人員對(duì)海洋牧場(chǎng)的影響這一獨(dú)特視角出發(fā),通過(guò)海洋牧場(chǎng)相關(guān)科學(xué)家、政府官員及從業(yè)者的深度訪談發(fā)現(xiàn),科學(xué)家與政府人員、從業(yè)者的互動(dòng)交流會(huì)受到其專業(yè)的影響,不同專業(yè)科學(xué)家對(duì)產(chǎn)業(yè)的關(guān)注點(diǎn)存在顯著差異。為保證產(chǎn)業(yè)良性發(fā)展,需要廣泛征集多領(lǐng)域科學(xué)家的見(jiàn)解。
由以上文獻(xiàn)梳理可知,學(xué)界對(duì)海洋牧場(chǎng)的相關(guān)研究呈現(xiàn)零散狀態(tài),研究成果的系統(tǒng)性偏弱,多側(cè)重于測(cè)算產(chǎn)出效率、技術(shù)效率及產(chǎn)量等。國(guó)外海洋牧場(chǎng)發(fā)展的經(jīng)驗(yàn)與教訓(xùn)有待深度挖掘提煉。政策研究方面?zhèn)戎赜诤Q竽翀?chǎng)經(jīng)濟(jì)子系統(tǒng)與環(huán)境子系統(tǒng)的單項(xiàng)政策擬定及該過(guò)程中的利益沖突問(wèn)題,對(duì)海洋牧場(chǎng)綜合生態(tài)系統(tǒng)缺乏生態(tài)圈與群落認(rèn)知,單一的經(jīng)濟(jì)視角或環(huán)境視角難以規(guī)避政策短視與非協(xié)同適配引致的合力降低。鑒于此,本研究運(yùn)用系統(tǒng)思維構(gòu)建中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)評(píng)測(cè)體系,借助系統(tǒng)動(dòng)力學(xué)模型,仿真出進(jìn)行系統(tǒng)優(yōu)化的5種政策模式,模擬異質(zhì)化政策模式下海洋牧場(chǎng)生態(tài)系統(tǒng)的發(fā)展趨勢(shì),通過(guò)施政結(jié)果對(duì)比分析進(jìn)行政策甄別與評(píng)價(jià),為現(xiàn)階段中國(guó)海洋牧場(chǎng)發(fā)展政策擬定與搭配提供論據(jù)支持與理念指導(dǎo)。
2中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)評(píng)測(cè)模型構(gòu)建
2.1海洋牧場(chǎng)生態(tài)系統(tǒng)評(píng)測(cè)指標(biāo)體系構(gòu)建
在生態(tài)經(jīng)濟(jì)系統(tǒng)概念影響下,學(xué)界將海洋漁業(yè)經(jīng)濟(jì)生態(tài)系統(tǒng)劃分為漁業(yè)生產(chǎn)系統(tǒng)(或經(jīng)濟(jì)系統(tǒng))與生態(tài)系統(tǒng),關(guān)注生產(chǎn)活動(dòng)與生態(tài)環(huán)境的相互作用[20]。現(xiàn)有與生態(tài)經(jīng)濟(jì)系統(tǒng)相關(guān)的系統(tǒng)動(dòng)力學(xué)研究成果會(huì)根據(jù)研究目的不同,擴(kuò)大系統(tǒng)范圍,融合科技、環(huán)境、資源等子系統(tǒng)[21-22]。如朱莊瑞等[23]為評(píng)價(jià)土地節(jié)約集約政策的有效性,劃分為行政效益、社會(huì)效益、經(jīng)濟(jì)效益子系統(tǒng),得到了不同維度的政策評(píng)價(jià)效果。鑒于此,本研究鎖定廣義的海洋牧場(chǎng)生態(tài)系統(tǒng),該系統(tǒng)是由經(jīng)濟(jì)子系統(tǒng)、科研子系統(tǒng)、水產(chǎn)技術(shù)推廣子系統(tǒng)、環(huán)境子系統(tǒng)構(gòu)成的綜合性復(fù)雜系統(tǒng)。各子系統(tǒng)相互擾動(dòng)影響,構(gòu)成綜合系統(tǒng)性突出的海洋牧場(chǎng)生態(tài)群落。在征詢專家意見(jiàn)及現(xiàn)有研究基礎(chǔ)上[16,24],各子系統(tǒng)的觀測(cè)指標(biāo)選擇綜合考慮了中國(guó)海洋牧場(chǎng)發(fā)展中變量間關(guān)系及數(shù)據(jù)可獲取性,經(jīng)過(guò)多輪篩選確定。經(jīng)濟(jì)子系統(tǒng)中選擇涉海就業(yè)人數(shù)、海水養(yǎng)殖面積、海水養(yǎng)殖產(chǎn)量、農(nóng)林漁業(yè)固定資產(chǎn)投資、GDP等指標(biāo),綜合反映海洋牧場(chǎng)建立及發(fā)展過(guò)程中涉及的人力資源、自然資源、投資與產(chǎn)量、產(chǎn)值等投入產(chǎn)出情況。構(gòu)建水產(chǎn)技術(shù)推廣子系統(tǒng)是由于技術(shù)水平與產(chǎn)出經(jīng)濟(jì)效益之間往往存在巨大鴻溝[25],水產(chǎn)技術(shù)推廣水平能夠折射出專業(yè)技術(shù)的普及應(yīng)用程度,關(guān)系到技術(shù)的實(shí)際經(jīng)濟(jì)產(chǎn)出。科研與水產(chǎn)技術(shù)推廣子系統(tǒng)主要選擇海洋科研機(jī)構(gòu)經(jīng)費(fèi)投入、海洋科研機(jī)構(gòu)專利、海洋科研機(jī)構(gòu)課題、水產(chǎn)技術(shù)推廣機(jī)構(gòu)數(shù)量、水產(chǎn)技術(shù)推廣實(shí)有人員情況等變量,兩個(gè)子系統(tǒng)通過(guò)海洋牧場(chǎng)科技水平這一變量作用于經(jīng)濟(jì)子系統(tǒng)。環(huán)境子系統(tǒng)主要選擇污染投資、污染處理及保護(hù)區(qū)建設(shè)方面的指標(biāo)。選定指標(biāo)參見(jiàn)表1。
2.2海洋牧場(chǎng)生態(tài)系統(tǒng)評(píng)測(cè)模型構(gòu)建與檢驗(yàn)
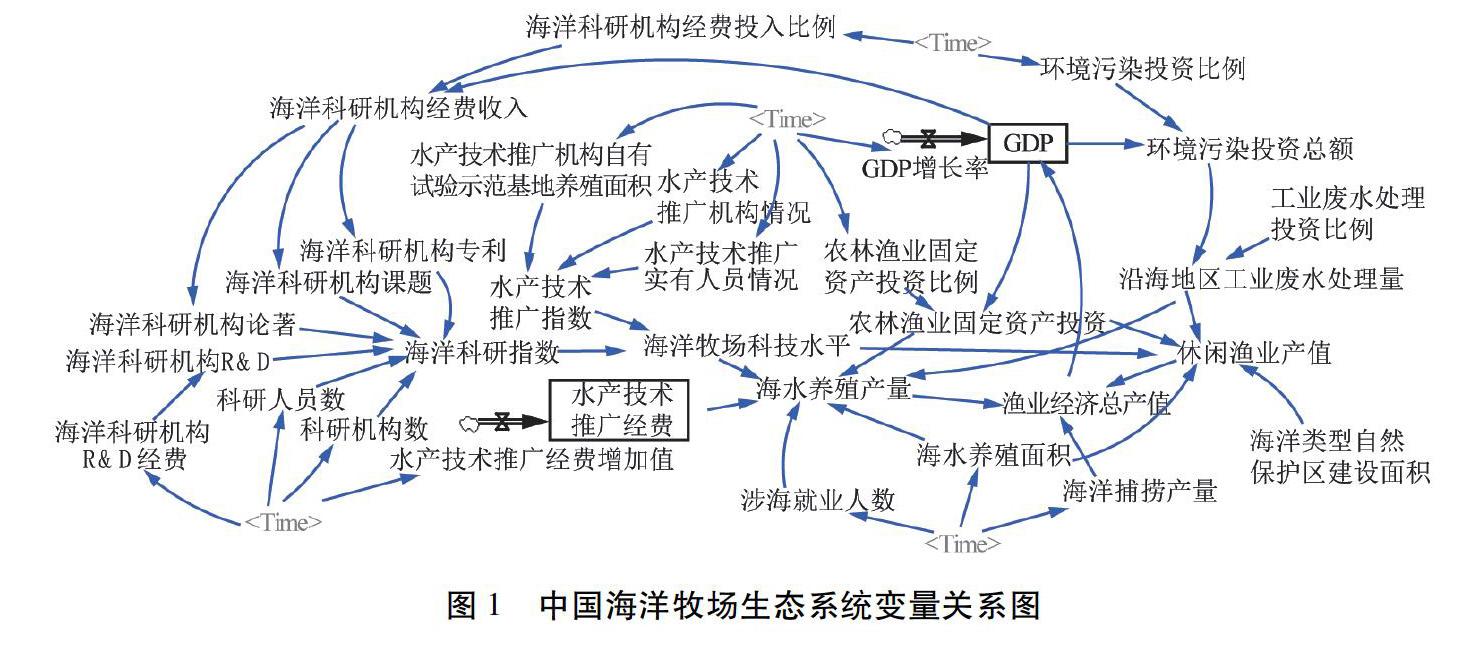
變量間關(guān)系方程構(gòu)建主要依賴基本函數(shù)關(guān)系、利用已有數(shù)據(jù)回歸等方法,對(duì)函數(shù)關(guān)系不明顯的變量間方程,主要利用Vensim中的表函數(shù)構(gòu)建。數(shù)據(jù)來(lái)源為2011—2017年的《中國(guó)統(tǒng)計(jì)年鑒》《中國(guó)海洋統(tǒng)計(jì)年鑒》《中國(guó)漁業(yè)統(tǒng)計(jì)年鑒》《中國(guó)環(huán)境統(tǒng)計(jì)年鑒》及相關(guān)統(tǒng)計(jì)公報(bào)等。基于系統(tǒng)動(dòng)力學(xué),構(gòu)建中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)模擬模型,詳見(jiàn)圖1。變量間主要反饋關(guān)系回路存在如下幾條:
第一,海洋科研機(jī)構(gòu)專利→海洋科研指數(shù)→海洋牧場(chǎng)科技水平→海水養(yǎng)殖產(chǎn)量→漁業(yè)經(jīng)濟(jì)總產(chǎn)值→GDP→海洋科研機(jī)構(gòu)經(jīng)費(fèi)收入→海洋科研機(jī)構(gòu)專利。
第二,沿海地區(qū)工業(yè)廢水處理量→海水養(yǎng)殖產(chǎn)量→漁業(yè)經(jīng)濟(jì)總產(chǎn)值→GDP→環(huán)境污染投資總額→沿海地區(qū)工業(yè)廢水處理量。
第三,沿海地區(qū)工業(yè)廢水處理量→休閑漁業(yè)產(chǎn)值→漁業(yè)經(jīng)濟(jì)總產(chǎn)值→GDP→環(huán)境污染投資總額→沿海地區(qū)工業(yè)廢水處理量。
第四,農(nóng)林漁業(yè)固定資產(chǎn)投資→海水養(yǎng)殖產(chǎn)量→漁業(yè)經(jīng)濟(jì)總產(chǎn)值→GDP→農(nóng)林漁業(yè)固定資產(chǎn)投資。
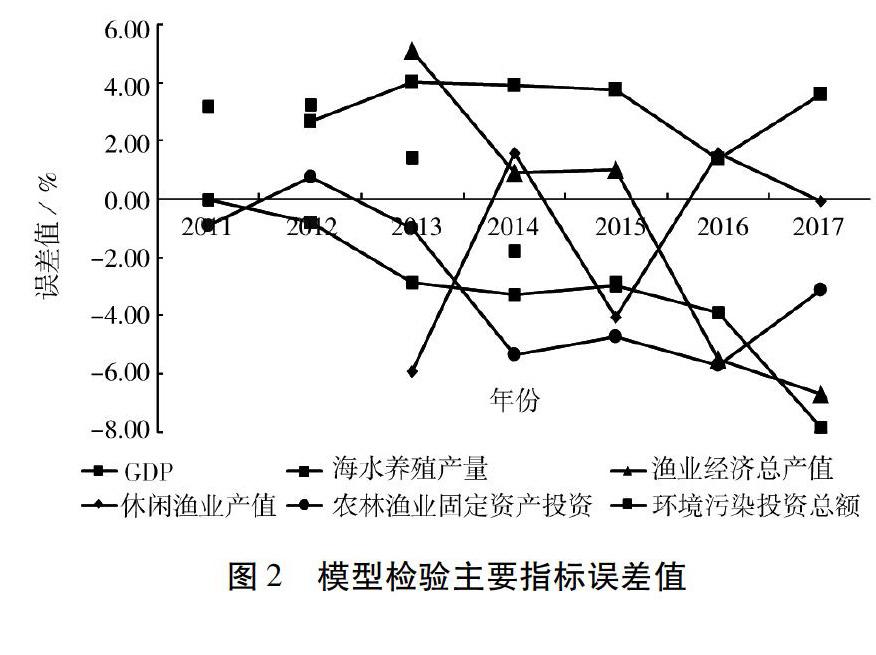
為保證所建系統(tǒng)能夠更貼切地模擬現(xiàn)實(shí),系統(tǒng)動(dòng)力學(xué)模型通過(guò)輸入初始真實(shí)值模擬并與現(xiàn)有數(shù)據(jù)進(jìn)行比對(duì)的方式進(jìn)行模型檢驗(yàn),但尚無(wú)統(tǒng)一誤差分析標(biāo)準(zhǔn)確定模型構(gòu)建是否優(yōu)良,通常在5%誤差水平即可接受。由于研究目的不同,部分指標(biāo)在10%左右誤差水平,主要觀測(cè)指標(biāo)模擬良好,依然可接受[22,26]。本模型檢驗(yàn)將2011年全國(guó)數(shù)據(jù)設(shè)置為初始值,模擬2011—2017年中國(guó)海洋牧場(chǎng)運(yùn)行狀況,主要指標(biāo)誤差情況見(jiàn)圖2。圖中主要指標(biāo)各年份誤差值基本在5%甚至2%水平以下,部分指標(biāo)誤差值高于5%但仍在可接受范圍內(nèi),故所有指標(biāo)(包括圖中未列出的)誤差值均在可接受范圍內(nèi),模擬效果良好,能夠較為真實(shí)客觀地反映中國(guó)海洋牧場(chǎng)運(yùn)行及發(fā)展情況。
3中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化政策仿真
3.1政策調(diào)節(jié)變量選取與參數(shù)賦值
海洋牧場(chǎng)生態(tài)系統(tǒng)不是簡(jiǎn)單的漁業(yè)養(yǎng)殖,而是三次產(chǎn)業(yè)融合、涉及政企學(xué)研農(nóng)等各方利益相關(guān)者的綜合性系統(tǒng)工程。僅依靠市場(chǎng)機(jī)制難以實(shí)現(xiàn)各項(xiàng)資源優(yōu)化配置,該系統(tǒng)的優(yōu)化與更新需要通過(guò)科學(xué)高效的政策組合激發(fā)政策績(jī)效來(lái)推動(dòng)實(shí)現(xiàn)。根據(jù)海洋牧場(chǎng)區(qū)(《國(guó)家級(jí)海洋牧場(chǎng)示范區(qū)建設(shè)規(guī)劃(2017—2025)》對(duì)全國(guó)沿海各省海洋牧場(chǎng)建設(shè)與發(fā)展計(jì)劃的說(shuō)明,確定天津、河北、遼寧、江蘇、浙江、福建、山東、廣東、廣西、海南沿海十省市為海洋牧場(chǎng)區(qū))的建設(shè)與成長(zhǎng)狀況,考量海洋牧場(chǎng)生態(tài)系統(tǒng)模擬模型中的變量,選取海洋科研機(jī)構(gòu)經(jīng)費(fèi)投入比例、水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率、水產(chǎn)技術(shù)推廣實(shí)有人員與機(jī)構(gòu)之比、環(huán)境污染投資比例、工業(yè)廢水處理投資比例作為政策調(diào)節(jié)變量。為排除對(duì)不同政策模式參數(shù)設(shè)置的主觀臆想,基于對(duì)海洋牧場(chǎng)區(qū)十省市數(shù)據(jù)(個(gè)別缺省年份數(shù)據(jù)由數(shù)據(jù)推算補(bǔ)足)的描述性統(tǒng)計(jì)分析來(lái)設(shè)計(jì)仿真方案。
海洋牧場(chǎng)十省市2011—2017年科研經(jīng)費(fèi)投入比例變化相對(duì)平緩。近5年,山東維持在10.0左右的較高水平,河北則低于1.0,其他省市基本在2.0~6.0之間(見(jiàn)圖3)。由于各省市不同年份水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率變化幅度較大,選取較為穩(wěn)定合理的變化值作為仿真參數(shù)。天津、山東、遼寧的水產(chǎn)技術(shù)推廣人員與機(jī)構(gòu)之比在2016年明顯降低,之后維持穩(wěn)定增長(zhǎng),其他省市一直保持在較穩(wěn)定水平(見(jiàn)圖4),研究選取2016—2017年均值作為參考值;環(huán)境污染投資比例除個(gè)別省市變化幅度較大,其他省市均穩(wěn)定在一定區(qū)間,可以0.75為界選取仿真參數(shù)(見(jiàn)圖5)。工業(yè)廢水處理投資比例由于相關(guān)數(shù)據(jù)缺省年份較多,處理方法同水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率指標(biāo)。
3.2政策模式仿真設(shè)計(jì)
依據(jù)海洋牧場(chǎng)現(xiàn)有管理政策體系,本研究嘗試設(shè)計(jì)5種政策模式進(jìn)行仿真(見(jiàn)表2)。原模式為海洋牧場(chǎng)發(fā)展當(dāng)前政策,政策組合的指標(biāo)取值依據(jù)闡釋如下:十八大提出建設(shè)海洋強(qiáng)國(guó)戰(zhàn)略以來(lái),海洋各產(chǎn)業(yè)的投入快速增長(zhǎng),海洋科研機(jī)構(gòu)經(jīng)費(fèi)投入比例由較低水平逐漸提升至較高水平,之后維持在6.00~7.50水平。2012年發(fā)布的全國(guó)水產(chǎn)技術(shù)推廣工作“十二五”規(guī)劃提出,改革水產(chǎn)技術(shù)推廣體系,將工作重心下移,使得水產(chǎn)技術(shù)推廣實(shí)有人員與機(jī)構(gòu)之比在長(zhǎng)期發(fā)展中處于穩(wěn)定比例。規(guī)劃提出積極落實(shí)2012年中央一號(hào)文件中關(guān)于“一個(gè)銜接,兩個(gè)覆蓋”政策,使得水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率獲得較大幅度提升,近兩年逐漸穩(wěn)定。十八大報(bào)告中強(qiáng)調(diào),要著力解決突出環(huán)境問(wèn)題,加強(qiáng)農(nóng)業(yè)面源污染防治,逐步改善先污染后治理的老模式,故環(huán)境污染投資比例依然處在較高水平,而工業(yè)廢水處理投資比例相對(duì)較低。
模式1在各維度上均保持了較高指標(biāo)水平,處于科技、環(huán)境投入較高、發(fā)展速度較快的理想政策配置水平。2017年,農(nóng)業(yè)部制定的《“十三五”漁業(yè)科技發(fā)展規(guī)劃》中提出了“兩大工程”:以科技引領(lǐng)海洋強(qiáng)國(guó)戰(zhàn)略,面向海洋漁業(yè)的科技創(chuàng)新工程和旨在促進(jìn)海洋漁業(yè)發(fā)展調(diào)結(jié)構(gòu)轉(zhuǎn)方式的水產(chǎn)技術(shù)推廣能力工程。加大科研投入并加強(qiáng)水產(chǎn)技術(shù)轉(zhuǎn)化推廣,故海洋牧場(chǎng)科技與技術(shù)指標(biāo)可能維持在高位。2016年,國(guó)務(wù)院印發(fā)的《“十三五”生態(tài)環(huán)境保護(hù)規(guī)劃》中強(qiáng)調(diào),逐步健全與完善生態(tài)文明建設(shè)體制機(jī)制,為環(huán)保釋放諸多紅利。因此,環(huán)境相關(guān)指標(biāo)可能維持在較高水平。
模式2相比模式1,調(diào)低了水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率水平。《“十三五”漁業(yè)科技發(fā)展規(guī)劃》強(qiáng)調(diào),重點(diǎn)建設(shè)水產(chǎn)技術(shù)推廣軟實(shí)力,發(fā)揮機(jī)制優(yōu)勢(shì),而不僅僅依賴高額資金投入,故未來(lái)政策動(dòng)向可能在水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率上有所調(diào)整。
模式3相比模式1,調(diào)低了環(huán)境相關(guān)指標(biāo)的投入。《“十三五”生態(tài)環(huán)境保護(hù)規(guī)劃》表明,在經(jīng)濟(jì)下行壓力加大情況下,部分地區(qū)環(huán)保相關(guān)投入可能減弱,借此調(diào)低環(huán)境相關(guān)變量水平作為政策變動(dòng)的一種可能性。
模式4相比模式1,調(diào)低了水產(chǎn)技術(shù)推廣實(shí)有人員與機(jī)構(gòu)之比。從年鑒數(shù)據(jù)來(lái)看,2015年,該指標(biāo)在一部分海洋牧場(chǎng)區(qū)出現(xiàn)明顯降低。《“十三五”漁業(yè)科技發(fā)展規(guī)劃》提出,推進(jìn)水產(chǎn)技術(shù)推廣體系公共服務(wù)能力建設(shè),建設(shè)重點(diǎn)示范基地,提高技術(shù)推廣人員素質(zhì)能力,不求數(shù)量求質(zhì)量,在此施政趨勢(shì)調(diào)整下,該指標(biāo)存在降低概率。
模式5相比模式1,調(diào)低了海洋科研機(jī)構(gòu)經(jīng)費(fèi)投入比例。模式5主要模擬經(jīng)濟(jì)下行壓力之下,科研機(jī)構(gòu)經(jīng)費(fèi)投入降低的情況。《“十三五”海洋領(lǐng)域科技創(chuàng)新專項(xiàng)規(guī)劃》強(qiáng)調(diào),海洋科研發(fā)展的總體思路之一是完善以企業(yè)為主體的海洋技術(shù)創(chuàng)新體系,促進(jìn)投入多元化。《“十三五”漁業(yè)科技發(fā)展規(guī)劃》也強(qiáng)調(diào)了未來(lái)要引導(dǎo)企業(yè)增加科技投入。由此可見(jiàn),政府對(duì)科研機(jī)構(gòu)經(jīng)費(fèi)投入有可能降低,通過(guò)投資主體組合優(yōu)化提升海洋科技創(chuàng)新效率。
4中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)發(fā)展態(tài)勢(shì)模擬
以2017年數(shù)據(jù)為初始值,選取海洋牧場(chǎng)科技水平、海水養(yǎng)殖產(chǎn)量、休閑漁業(yè)產(chǎn)值、漁業(yè)經(jīng)濟(jì)總產(chǎn)值為主要觀測(cè)變量,其他作為輔助解釋變量進(jìn)行海洋牧場(chǎng)生態(tài)系統(tǒng)模擬預(yù)測(cè)。海洋牧場(chǎng)科技水平由海洋科研與水產(chǎn)技術(shù)推廣相關(guān)變量復(fù)合構(gòu)建,綜合反映海洋牧場(chǎng)科技的長(zhǎng)期發(fā)展。海水養(yǎng)殖產(chǎn)量、漁業(yè)經(jīng)濟(jì)總產(chǎn)值為衡量海洋牧場(chǎng)產(chǎn)出的顯性指標(biāo)。休閑漁業(yè)作為一種多產(chǎn)業(yè)融合的新業(yè)態(tài),不僅反映海洋牧場(chǎng)的經(jīng)濟(jì)產(chǎn)出,還能折射出牧場(chǎng)區(qū)的生態(tài)環(huán)境狀況。運(yùn)用Vensim PLE軟件,模擬2017—2035年所設(shè)5種政策模式下的海洋牧場(chǎng)發(fā)展態(tài)勢(shì),主要觀測(cè)指標(biāo)的模擬結(jié)果見(jiàn)圖6~圖9。
觀察圖6~圖9可知,原模式(現(xiàn)有政策組合)的4項(xiàng)主要觀測(cè)變量的模擬值基本處于中游水平。在復(fù)雜系統(tǒng)的運(yùn)維過(guò)程中,各子系統(tǒng)的高效協(xié)同尤為重要,亟待探尋中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化政策群的最優(yōu)投入產(chǎn)出比。
首先,模式1下各觀測(cè)變量處于較好發(fā)展水平,符合該政策模式下最優(yōu)參數(shù)設(shè)置。在豐沛的科研與水產(chǎn)技術(shù)推廣相關(guān)資源投入下,海洋牧場(chǎng)科技水平穩(wěn)步提升。環(huán)境投入增加有效改善了牧場(chǎng)環(huán)境水平,海洋牧場(chǎng)的海水養(yǎng)殖產(chǎn)量、休閑漁業(yè)產(chǎn)值、漁業(yè)經(jīng)濟(jì)總產(chǎn)值呈現(xiàn)較快增長(zhǎng)。
其次,模式2盡管調(diào)低了水產(chǎn)技術(shù)推廣經(jīng)費(fèi)增長(zhǎng)率,在海洋科研機(jī)構(gòu)高投入、多人員推廣的條件下,牧場(chǎng)海水養(yǎng)殖產(chǎn)量及休閑漁業(yè)穩(wěn)步發(fā)展,帶動(dòng)漁業(yè)經(jīng)濟(jì)總產(chǎn)值提升。表明政府水產(chǎn)技術(shù)推廣經(jīng)費(fèi)投入對(duì)海洋牧場(chǎng)生態(tài)系統(tǒng)運(yùn)維的經(jīng)濟(jì)性效用較為有限,引導(dǎo)多機(jī)構(gòu)、多組織、多企業(yè)參與水產(chǎn)技術(shù)推廣,實(shí)現(xiàn)投入多元化與收益分配比例調(diào)整能夠有效提升海洋牧場(chǎng)科技水平。中國(guó)水產(chǎn)技術(shù)推廣體系正逐步趨于完善,推廣工作體制改革方向明確,能夠在有限資源投入下最大限度地發(fā)揮水產(chǎn)技術(shù)推廣機(jī)構(gòu)與人員效用。
再者,模式3的低投入環(huán)境政策導(dǎo)致海水養(yǎng)殖產(chǎn)量、休閑漁業(yè)產(chǎn)值在未來(lái)增速放緩,甚至低于現(xiàn)行發(fā)展政策模式增速,使得漁業(yè)經(jīng)濟(jì)總產(chǎn)值整體增速顯著降低。模式3與改變科技政策的模式2、4、5相比,對(duì)海洋牧場(chǎng)經(jīng)濟(jì)產(chǎn)出的負(fù)向影響更為凸顯。海洋環(huán)境是海洋牧場(chǎng)生態(tài)系統(tǒng)健康運(yùn)行的重要基礎(chǔ),也是海洋生態(tài)文明的核心要素。環(huán)境投入增加,生態(tài)環(huán)境質(zhì)量提升,能夠促進(jìn)海洋牧場(chǎng)經(jīng)濟(jì)系統(tǒng)有序健康發(fā)展[27];反之,忽略環(huán)境投入,破壞了海洋牧場(chǎng)生態(tài)群落賴以生存的根基,將會(huì)影響整個(gè)沿海地區(qū)經(jīng)濟(jì)與社會(huì)發(fā)展。不僅如此,圖6顯示,模式3在未改變科技相關(guān)政策的情況下,海洋牧場(chǎng)科技水平也有一定程度下降,主要是經(jīng)濟(jì)發(fā)展緩慢導(dǎo)致其他投入降低造成,更加印證了環(huán)境投入關(guān)系到海洋牧場(chǎng)生態(tài)系統(tǒng)的可持續(xù)性發(fā)展,應(yīng)持續(xù)不間斷、有計(jì)劃地投入。
值得注意的是,調(diào)低了水產(chǎn)技術(shù)推廣實(shí)有人員與機(jī)構(gòu)之比和海洋科研投入的模式4與模式5。模式4與模式5在主要觀測(cè)變量發(fā)展態(tài)勢(shì)模擬值上產(chǎn)生重大分化,提供了政策模式調(diào)整的關(guān)鍵提示信息。觀察圖6,兩者的海洋牧場(chǎng)科技水平在2022年以前均低于現(xiàn)行政策模式,模式4略高;在2022年以后,模式4的海洋牧場(chǎng)科技水平發(fā)展超過(guò)了原模式,而模式5依然低位運(yùn)行。這說(shuō)明與水產(chǎn)技術(shù)推廣工作相比,科研投入對(duì)海洋牧場(chǎng)科技發(fā)展速度與水平起決定性作用。由圖7可知,2023年左右,模式5與模式4的海水養(yǎng)殖產(chǎn)量增速產(chǎn)生較大差異:模式4在海洋科研高投入之下,海水養(yǎng)殖產(chǎn)量增速加快,僅次于最優(yōu)狀態(tài)的模式1;低科研投入下的模式5則一直保持低于現(xiàn)行發(fā)展模式的增長(zhǎng)率。圖8顯示出模式4的休閑漁業(yè)產(chǎn)值高于模式5,均高于原模式并呈現(xiàn)出加速上升趨勢(shì)。圖9中的兩大模式下的漁業(yè)經(jīng)濟(jì)總產(chǎn)值也存在顯著差異,模式4的增速明顯高于模式5。從休閑漁業(yè)與海洋經(jīng)濟(jì)產(chǎn)值兩大經(jīng)濟(jì)子系統(tǒng)的指標(biāo)來(lái)看,模式4對(duì)經(jīng)濟(jì)效應(yīng)的提升更為立竿見(jiàn)影。通過(guò)模式4與模式1比較,兩者的海水養(yǎng)殖產(chǎn)量、休閑漁業(yè)產(chǎn)值、漁業(yè)經(jīng)濟(jì)總產(chǎn)值增長(zhǎng)速度相差不大,結(jié)合模式2的模擬仿真結(jié)果可以得出,龐大的水產(chǎn)技術(shù)推廣人員隊(duì)伍、水產(chǎn)技術(shù)推廣經(jīng)費(fèi)的高投入并不一定能夠快速高效地提升中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)的產(chǎn)出與發(fā)展水平。水產(chǎn)技術(shù)推廣體系革新、水產(chǎn)技術(shù)推廣工程建設(shè)、水產(chǎn)技術(shù)推廣服務(wù)體系完善等軟實(shí)力提升才是成本約束下最大化收益的最優(yōu)政策選擇。
從前瞻性視角考量,經(jīng)過(guò)多角度對(duì)比分析可知,模式4相比各項(xiàng)投入最優(yōu)的模式1,更為符合中國(guó)海洋牧場(chǎng)發(fā)展現(xiàn)狀與趨勢(shì),政策適應(yīng)性強(qiáng),投入產(chǎn)出比較為理想,是成本約束下收益較高的施政選擇。
5研究結(jié)論與政策啟示
首先,從可持續(xù)發(fā)展視角看,中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)尚處于初級(jí)發(fā)展階段,海洋牧場(chǎng)生態(tài)系統(tǒng)良性發(fā)展在較大程度上依賴于海洋科研與環(huán)境投入。但高科研投入不能彌補(bǔ)環(huán)境投入過(guò)低對(duì)海洋牧場(chǎng)生態(tài)系統(tǒng)造成的不可逆轉(zhuǎn)的毀壞性影響,過(guò)低的環(huán)境投入通過(guò)影響經(jīng)濟(jì)產(chǎn)出導(dǎo)致牧場(chǎng)科技水平貶損。關(guān)于環(huán)境與科技投入的側(cè)重點(diǎn)選擇,歐盟海洋牧場(chǎng)的成功經(jīng)驗(yàn)可資借鑒。
其次,系統(tǒng)仿真模擬結(jié)果表明,海洋科研高投入為海洋牧場(chǎng)帶來(lái)的經(jīng)濟(jì)產(chǎn)出收益大于水產(chǎn)技術(shù)推廣人員與經(jīng)費(fèi)高投入的收益,海洋科研高投入所帶來(lái)的技術(shù)成果雖然短期內(nèi)難以快速轉(zhuǎn)化為實(shí)際經(jīng)濟(jì)產(chǎn)出,但從長(zhǎng)期看,海洋科研的持續(xù)性投入能夠通過(guò)技術(shù)轉(zhuǎn)型升級(jí)助推牧場(chǎng)環(huán)境友好性提升。現(xiàn)存的水產(chǎn)技術(shù)推廣體系存在人員結(jié)構(gòu)不合理、經(jīng)費(fèi)投入邊際收益低、技術(shù)轉(zhuǎn)化遭遇瓶頸等問(wèn)題,其中,水產(chǎn)技術(shù)推廣人員隊(duì)伍建設(shè)與再培訓(xùn)為薄弱環(huán)節(jié)。
再者,模擬仿真結(jié)果結(jié)合牧場(chǎng)區(qū)描述性統(tǒng)計(jì)分析可知,河北、海南、江蘇、浙江、福建牧場(chǎng)區(qū)的海洋科研投入比例相對(duì)較低,可能會(huì)影響海洋牧場(chǎng)產(chǎn)出增長(zhǎng)速率;天津、河北、海南的水產(chǎn)技術(shù)推廣人員與機(jī)構(gòu)之比較高,結(jié)合其水產(chǎn)技術(shù)推廣機(jī)構(gòu)數(shù)量并不多的情況來(lái)看,可能存在單一機(jī)構(gòu)人員冗余、機(jī)構(gòu)服務(wù)覆蓋范圍狹窄等癥結(jié)。
通過(guò)對(duì)中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化政策進(jìn)行仿真,提出現(xiàn)有政策文件精神倡導(dǎo)下的高概率政策組合,依據(jù)政策模式情形下牧場(chǎng)發(fā)展態(tài)勢(shì)模擬分析結(jié)果,從以下幾方面嘗試進(jìn)行政策創(chuàng)新搭配與時(shí)機(jī)審度:
第一,設(shè)計(jì)構(gòu)建激勵(lì)環(huán)境保護(hù)與科技創(chuàng)新協(xié)同發(fā)展的政策模式。2019年的《政府工作報(bào)告》強(qiáng)調(diào),實(shí)現(xiàn)綠色發(fā)展,構(gòu)建現(xiàn)代化經(jīng)濟(jì)體系尤為重要。要“加強(qiáng)污染防治重大科技攻關(guān)”、“協(xié)同高質(zhì)量發(fā)展與生態(tài)環(huán)境保護(hù)”。在海洋牧場(chǎng)發(fā)展過(guò)程中,環(huán)境保護(hù)與開(kāi)發(fā)的持續(xù)投入能有效保持牧場(chǎng)生態(tài)群落健康,形成由經(jīng)濟(jì)子系統(tǒng)向海洋牧場(chǎng)科技投入的正反饋。狠抓牧場(chǎng)區(qū)污染源防治,逐步構(gòu)建“大投入治污染,強(qiáng)措施防污染,高科技杜絕污染”模式。海洋牧場(chǎng)推廣使用的適用性科技不但要提產(chǎn)量,更要保環(huán)境。將環(huán)境測(cè)評(píng)因素納入科技成果評(píng)定體系中,發(fā)揮科技水平提升與環(huán)境優(yōu)化的外部經(jīng)濟(jì)性,涵養(yǎng)海洋牧場(chǎng)各生態(tài)子系統(tǒng)良性運(yùn)行的根基。
第二,穩(wěn)步提升海洋牧場(chǎng)直接與間接科研投入,健全完善“政企學(xué)研”多元融合的水產(chǎn)技術(shù)推廣投入機(jī)制。海洋科研投入較低的省市,如河北、海南、江蘇、浙江、福建,在加大海洋科研相關(guān)經(jīng)費(fèi)投入的同時(shí),要賦予海洋科研機(jī)構(gòu)、高校、科研團(tuán)隊(duì)更多研究自主權(quán),脫離“經(jīng)費(fèi)限制成果,賦權(quán)限制研究”的科研窘境,調(diào)動(dòng)涉海類高校、科研院所及涉海企業(yè)的研發(fā)積極性,提升科研人員成果獎(jiǎng)勵(lì)力度的同時(shí)優(yōu)化項(xiàng)目審核與監(jiān)督機(jī)制。在水產(chǎn)技術(shù)推廣方面,集中資源投入建設(shè)海洋牧場(chǎng)產(chǎn)業(yè)創(chuàng)新發(fā)展的重點(diǎn)工程、示范工程,引導(dǎo)企業(yè)、高校、研究機(jī)構(gòu)等組織積極投入,盡快扭轉(zhuǎn)水產(chǎn)技術(shù)推廣投入“沒(méi)方向、無(wú)針對(duì)、沒(méi)轉(zhuǎn)化”的局面。
第三,大力推進(jìn)水產(chǎn)技術(shù)推廣體系改革常態(tài)化、水產(chǎn)技術(shù)推廣工作專業(yè)化與水產(chǎn)技術(shù)推廣服務(wù)信息化。《全國(guó)水產(chǎn)技術(shù)推廣工作“十三五”規(guī)劃》對(duì)水產(chǎn)技術(shù)推廣改革創(chuàng)新能力,提出了由體制到具體工作的細(xì)化要求,指出水產(chǎn)技術(shù)推廣信息服務(wù)是發(fā)展的一大亮點(diǎn)。海洋牧場(chǎng)水產(chǎn)技術(shù)推廣體系的改革創(chuàng)新應(yīng)專注于基層推廣體系改革,工作機(jī)制、人才培養(yǎng)方式創(chuàng)新及組織結(jié)構(gòu)優(yōu)化。通過(guò)標(biāo)準(zhǔn)化體系規(guī)范水產(chǎn)技術(shù)推廣工作,編制水產(chǎn)技術(shù)推廣工作手冊(cè)以明確工作細(xì)則與標(biāo)準(zhǔn)。打造海洋牧場(chǎng)區(qū)大數(shù)據(jù)平臺(tái)為政企投入精準(zhǔn)化提供數(shù)據(jù)支持,開(kāi)發(fā)適用于技術(shù)推廣工作人員與養(yǎng)殖人員的牧場(chǎng)區(qū)專用APP,提高技術(shù)使用便捷性。
第四,構(gòu)建水產(chǎn)技術(shù)推廣人才特色化培養(yǎng)體系,通過(guò)國(guó)內(nèi)外交流提升推廣人員綜合素質(zhì),掌握實(shí)用技能。海洋牧場(chǎng)建設(shè)對(duì)水產(chǎn)技術(shù)推廣人員提出更高要求,尤其針對(duì)天津、河北、海南等在技術(shù)推廣人員結(jié)構(gòu)、質(zhì)量上存在問(wèn)題的海洋牧場(chǎng)區(qū)而言,精簡(jiǎn)實(shí)有人員、提高技術(shù)推廣人員素質(zhì)迫在眉睫。貫徹落實(shí)《農(nóng)業(yè)技術(shù)推廣法》“一個(gè)銜接,兩個(gè)覆蓋”的要求,秉承“機(jī)制打磨隊(duì)伍,交流提升人才”的原則,構(gòu)建“嚴(yán)格選拔,深入培養(yǎng),重點(diǎn)提升”的人才隊(duì)伍建設(shè)機(jī)制。打造融合政府、企業(yè)、高校、項(xiàng)目于一體的水產(chǎn)技術(shù)推廣人才交流平臺(tái),建立與漁業(yè)大國(guó)、國(guó)際漁業(yè)相關(guān)組織的“朋友圈”,形成人才“理論學(xué)習(xí),推廣實(shí)踐,對(duì)外交流”的長(zhǎng)效循環(huán)培養(yǎng)體系。
星羅棋布的海洋牧場(chǎng)是激發(fā)海洋經(jīng)濟(jì)活力的試驗(yàn)田、中國(guó)藍(lán)色糧倉(cāng)的重要組成部分,未來(lái)將向以深遠(yuǎn)海養(yǎng)殖業(yè)為主體的“深藍(lán)漁業(yè)”發(fā)展。中國(guó)海洋牧場(chǎng)發(fā)展特色鮮明但基礎(chǔ)較為薄弱,既有先進(jìn)經(jīng)驗(yàn)可循,便應(yīng)進(jìn)行優(yōu)質(zhì)基因的變通汲取。海洋牧場(chǎng)發(fā)展應(yīng)遵循生態(tài)系統(tǒng)規(guī)律,經(jīng)由陸海一體化統(tǒng)籌發(fā)展理念引領(lǐng),在未來(lái)發(fā)展趨勢(shì)明朗的前提下,開(kāi)展政策評(píng)價(jià)與搭配演練,發(fā)揮政策效能綜合治理陸海污染,保障海產(chǎn)品食品安全與牧場(chǎng)產(chǎn)出質(zhì)量,以成本最小化實(shí)現(xiàn)中國(guó)海洋牧場(chǎng)生態(tài)系統(tǒng)優(yōu)化與可持續(xù)發(fā)展。
(編輯:劉照勝)
參考文獻(xiàn)
[1]韓楊. 1949年以來(lái)中國(guó)海洋漁業(yè)資源治理與政策調(diào)整[J]. 中國(guó)農(nóng)村經(jīng)濟(jì), 2018(9):14-28.
[2]韓楊, CURTIS R. 美國(guó)海洋漁業(yè)資源開(kāi)發(fā)的主要政策與啟示[J]. 農(nóng)業(yè)經(jīng)濟(jì)問(wèn)題, 2017,38(8):103-109.
[3]PITA P, VILLASANTE S, ARLINGHAUS R, et al. A matter of scales: does the management of marine recreational fisheries follow the ecosystem approach to fisheries in Europe?[J]. Marine policy, 2018,97:61-71.
[4]SOUTHWICK R, HOLDSWORTH J C, REA T, et al. Estimating marine recreational fishings economic contributions in New Zealand[J]. Fisheries research, 2018,208:116-123.
[5]SIDDIKI S, GOEL S. A stakeholder analysis of U.S. marine aquaculture partnerships[J]. Marine policy, 2015,57:93-102.
[6]FAIRBANKS L. Moving mussels offshore? perceptions of offshore aquaculture policy and expansion in New England[J]. Ocean & coastal management, 2016,130:1-12.
[7]VIANNA L F D N, FILHO J B. Spatial analysis for site selection in marine aquaculture: an ecosystem approach applied to Baía Sul, Santa Catarina, Brazil[J]. Aquaculture, 2018,489:162-174.
[8]YU J, YIN W. Exploring stakeholder engagement in mariculture development: challenges and prospects for China[J]. Marine policy, 2019,103:84-90.
[9]LINDLAND K M, GJERSTAD B, KRVEL A V, et al. Governing for sustainability in the Norwegian aquaculture industry[J]. Ocean & coastal management, 2019,179:104827.
[10]GREALIS E, HYNES S, O DONOGHUE C, et al. The economic impact of aquaculture expansion: an inputoutput approach[J]. Marine policy, 2017,81:29-36.
[11]GARZAGIL M D, SURSREGUEIRO J C, VARELALAFUENTE M M. Using inputoutput methods to assess the effects of fishing and aquaculture on a regional economy: the case of Galicia, Spain[J]. Marine policy, 2017,85:48-53.
[12]GUILLEN J, ASCHE F, CARVALHO N, et al. Aquaculture subsidies in the European Union: evolution, impact and future potential for growth[J]. Marine policy, 2019,104:19-28.
[13]ANNEBOINA L R, KAVI KUMAR K S. Economic analysis of mangrove and marine fishery linkages in India[J]. Ecosystem services, 2017,24:114-123.
[14]HOLDEN J J, COLLICUTT B, COVERNTON G, et al. Synergies on the coast: challenges facing shellfish aquaculture development on the central and north coast of British Columbia[J]. Marine policy, 2019,101:108-117.
[15]DAVIES I P, CARRANZA V, FROEHLICH H E, et al. Governance of marine aquaculture: Pitfalls, potential, and pathways forward[J]. Marine policy, 2019,104:29-36.
[16]胡求光, 王秀娟, 曹玲玲. 中國(guó)藍(lán)色牧場(chǎng)發(fā)展?jié)摿Φ氖‰H時(shí)空差異分析[J]. 中國(guó)農(nóng)村經(jīng)濟(jì), 2015(5):70-81.
[17]梁鑠, 陳琦, 韓立民. 中國(guó)“藍(lán)色糧倉(cāng)”生產(chǎn)潛力評(píng)估研究[J]. 農(nóng)村經(jīng)濟(jì), 2018(6):49-54.
[18]HOFHERR J, NATALE F, TRUJILLO P. Is lack of space a limiting factor for the development of aquaculture in EU coastal areas?[J]. Ocean & coastal management, 2015,116:27-36.
[19]SAFFORD T G, VIEIRA P F, POLETTE M. Scientific engagement and the development of marine aquaculture in Santa Catarina, southern Brazil[J]. Ocean & coastal management, 2019,178:104840.
[20]秦宏, 張瑩. 國(guó)外漁業(yè)生態(tài)經(jīng)濟(jì)相關(guān)研究述評(píng)[J]. 經(jīng)濟(jì)問(wèn)題, 2016(9):15-21.
[21]周雄勇, 許志端, 郗永勤. 中國(guó)節(jié)能減排系統(tǒng)動(dòng)力學(xué)模型及政策優(yōu)化仿真[J]. 系統(tǒng)工程理論與實(shí)踐, 2018,38(6):1422-1444.
[22]楊紅娟, 張成浩. 基于系統(tǒng)動(dòng)力學(xué)的云南生態(tài)文明建設(shè)有效路徑研究[J]. 中國(guó)人口·資源與環(huán)境, 2019,29(2):16-24.
[23]朱莊瑞,呂萍.中國(guó)城市土地節(jié)約集約利用政策有效性區(qū)域差異研究[J].中國(guó)人口·資源與環(huán)境,2015,25(12):129-137.
[24]狄乾斌, 梁倩穎. 中國(guó)海洋生態(tài)效率時(shí)空分異及其與海洋產(chǎn)業(yè)結(jié)構(gòu)響應(yīng)關(guān)系識(shí)別[J]. 地理科學(xué), 2018,38(10):1606-1615.
[25]王林輝, 袁禮. 有偏型技術(shù)進(jìn)步、產(chǎn)業(yè)結(jié)構(gòu)變遷和中國(guó)要素收入分配格局[J]. 經(jīng)濟(jì)研究, 2018,53(11):115-131.
[26]曾麗君, 隋映輝, 申玉三. 科技產(chǎn)業(yè)與資源型城市可持續(xù)協(xié)同發(fā)展的系統(tǒng)動(dòng)力學(xué)研究[J]. 中國(guó)人口·資源與環(huán)境, 2014,24(10):85-93.
[27]孫劍鋒, 秦偉山, 孫海燕, 等. 中國(guó)沿海城市海洋生態(tài)文明建設(shè)評(píng)價(jià)體系與水平測(cè)度[J]. 經(jīng)濟(jì)地理, 2018,38(8):19-28.
[28]GARZAGIL M D, VZQUEZRODRGUEZ M X, VARELALAFUENTE M M. Marine aquaculture and environment quality as perceived by Spanish consumers: the case of shellfish demand[J]. Marine policy, 2016,74:1-5.
[29]BOERLAGE A S, NGUYEN K V, DAVIDSON J, et al. Finfish marine aquaculture in northern Vietnam: factors related to pathogen introduction and spread[J]. Aquaculture, 2017,466:1-8.
[30]王嵩, 孫才志, 范斐. 基于共生理論的中國(guó)沿海省市海洋經(jīng)濟(jì)生態(tài)協(xié)調(diào)模式研究[J]. 地理科學(xué), 2018,38(3):342-350.
[31]胡玉璽, 吳曉磊, 馬世昌,等. 濕地“三生”空間耦合的系統(tǒng)動(dòng)力學(xué)模型實(shí)證分析——以西溪國(guó)家濕地公園為例[J]. 經(jīng)濟(jì)地理, 2018,38(7):173-180.
[32]胡偉, 韓增林, 葛岳靜,等. 基于能值的中國(guó)海洋生態(tài)經(jīng)濟(jì)系統(tǒng)發(fā)展效率[J]. 經(jīng)濟(jì)地理, 2018,38(8):162-171.
[33]史丹, 王俊杰. 基于生態(tài)足跡的中國(guó)生態(tài)壓力與生態(tài)效率測(cè)度與評(píng)價(jià)[J]. 中國(guó)工業(yè)經(jīng)濟(jì), 2016(5):5-21.
AbstractUnder the background of resource exhaustion, production imbalance and negative ecological effect of marine fishery industry of China, marine ranch ecosystem has become an indispensable and important entity to support the blue granary strategy. It has promoted the development of marine economy and ecology. Stimulating the driving force of marine ranch policy and the developmental potential, replacing old growth drivers with new ones, upgrading and transforming the fishery industry have become the core elements to promote the connotative development of marine economy of China. The author have selected subsystems and evaluation indexes of the marine ranch ecosystem and constructed the system dynamics model to analyze the multivariate relationships of the ecosystem. The varieties of policy adjustment on marine ranch are selected to simulate the trends of marine ranch ecosystem of China in 2017-2035 through five kinds of policyoptimizing models. The conclusions can be obtained by comparison analysis. The significant differences in the input of marine scientific research and the construction of aquatic technology promoting staff and institutions among ten Coastal provinces have been shown. The benign development of marine ranch ecosystem depends on marine scientific research and environmental investment. The continuous investment in environmental protection and upgrading should be strengthen. The input of marine scientific research can improve the environmental quality through technology upgrading.However, the level of input and output efficiency of aquatic technology promotion is low. It shows that more attention should be paid to the construction and retraining of aquaculture technology promoting staff. The cooperative effect between technology policy and environmental policy is the key to improve policy performance. The ‘governmententerpriseuniversityresearch multiinput model should be built and improved. The normalization, professionalization and informationization of the reform of aquaculture technology promotion should be accelerated. Taking the extraterritorial experience as an opportunity to build a characteristic system for training talents in aquatic technology. The policy model should be done by updating policy adaptation and connection details which can accomplish the collaborative development of the environmental protection of marine ranch ecosystem and the innovation of science and technology.
Key wordsmarine ranch; ecosystem; system dynamics; policy simulation; system simulation

