高中數學建模的教學與探究
溫茜茜

摘 要:本文對新高考模式下高中數學建模教學進行教學探究,文中以2008年美國中學生數學建模B題的抑制城市犯罪暴力問題為案例,在此建立回歸分析數學模型對數據資料進行相關分析和預測.在構建解題的研究過程,針對高中學數學建模,介紹回歸分析類型問題解決的建模方法和技巧,包括回歸分析的類型、原理算法、編程計算、分析解決問題,培養和提高中學生數學建模能力。
關鍵詞:新高考;高中數學;建模教學
一、回歸分析模型
(一)問題的提出
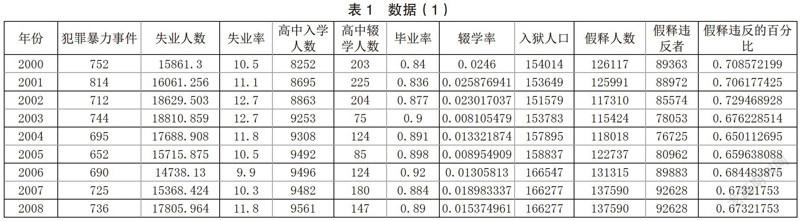
犯罪暴力事件,失業人數,失業率,高中入學人數,高中輟學人數,畢業率,輟學率,入獄人口,假釋人數,假釋違反者,假釋違反的百分比.對這些數據進行分析和建模,并為城市制定計劃以減少犯罪暴力。
(二)回歸分析基本類型及原理
變量之間的相互關系可分為確定性關系,也叫做函數關系,其特征是:一個變量隨著其他變量的確定而確定;另一類關系叫相關關系,其特征是:變量之間的關系很難用一種精確的方法表示出來.由于存在測量誤差等原因,或當對事物內部規律了解得更加深刻時,確定性關系和相關關系可能互相轉化.
回歸分析就是處理變量之間的相關關系的一種數學方法,是最常用的數理統計方法,能解決預測、控制、生產工藝優化等問題,有著廣泛應用.回歸分析一般分為線性回歸分析與非線性回歸分析.
線性回歸又分一元線性回歸和多元線性回歸,其中一元線性回歸為一個自變量,其模型是y=a+bx+ε,其中a為截距、b為回歸直線的斜率,它們稱回歸系數,ε是隨機誤差.多元線性回歸的自變量為多個,其模型是,其中b0是常數項,稱為y對應于的偏回歸系數,ε是隨機誤差.有時兩個變量之間的關系可以不是線性的相關關系,而是某種曲線的相關關系,這種情況則需要構建曲線回歸分析模型.
非線性回歸即為曲線回歸,又分為一元非線形和多元非線形.一元非線形回歸(曲線回歸)指的是一個自變量的非線形回歸,主要有對數、反函數、拋物線、三次、復合、冪函數、指數、logistics等曲線方程.多元非線形回歸指的是自變量有兩個或兩個以上的非線形回歸.常見的六類曲線代換方法如下:
(1)雙曲線;(2)冪函數曲線;(3)指數曲線,其中a>0;(4)倒指數曲線;(5)對數曲線,x>0;(6)S型曲線
(三)回歸分析解題方法
回歸分析的大概解題方法和步驟如下:
(1)數據整理(包含因變量和自變量);
(2)選定因變量與自變量之間的模型(根據數據特征結合經驗構建數學式子),利用數據按照最小二乘準則計算模型中的系數;
(3)利用統計分析方法對不同的模型進行比較,找出與數據擬合得最好得模型;
(4)判斷得到的模型是否適合于這組數據;
(5)利用模型對因變量作出解釋或預測.
(四)解題并得出結論
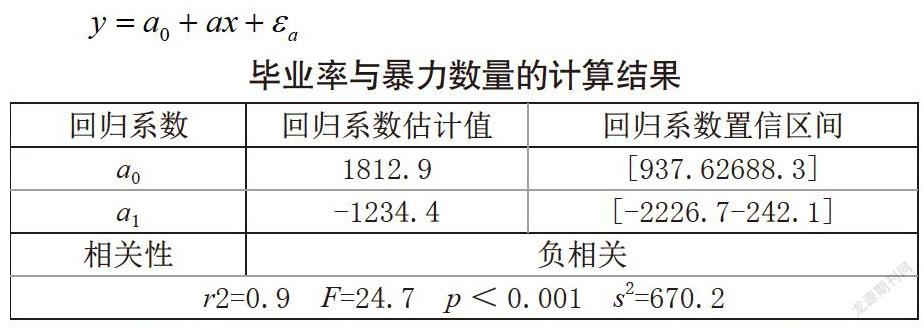
根據散點圖及經驗構建畢業率關于暴力數量的一元線性回歸模型:
處理數據后,經過殘差分析和檢驗,從相關性分析與回歸分析的結果來看,畢業率與暴力事件相關,且呈現負相關.當畢業率越低,暴力事件越高;畢業率高,暴力事件數量降低.接著對其進行回歸預測,可得出暴力事件數量下降,畢業率要呈增長趨勢.
二、對教材相關內容的分析
新課標人教版數學必修1第三章第二節函數模型及其應用就安排了用回歸分析的方法來解決問題的內容如汽車速率問題、人口增長問題、桶裝水銷售利潤問題、身高體重問題等,用學生已經學習過的一次函數、二次函數、指數函數等來擬合并解決問題.高考中也出現了需要用回歸分析的方法解決的問題.
參考文獻
[1]孟振蘋.高中數學建模的教學方法與策略研究[D].河南師范大學,2014.
[2]趙靜,但琦等.數學建模與數學實驗(第三版)[M]..北京:高等教育出版社,2008.254-280.
[3]王蕊,董祥旻,何衛蘋.一種多元非線性回歸模型的建立方法及其應用[J].中國考試,2010,11:17-22.

