淺談初中數學常見探索性問題及解法
李佩鸞

【摘要】近幾年各地中考試卷中涌現出形式多樣的探索性試題,它既能充分地考查學生基礎知識掌握的熟練程度,又能較好地考查學生的觀察、分析、比較、概括的能力,發散思維能力、探索發現能力、獨立創新能力和解決實際問題的能力等。探索型題一般沒有明確結論,沒有固定的形式和方法,要求學生通過自己的觀察、分析、比較、概括、得出結論,并加以論證結論的正確性。常見的探索性試題大致有3種:條件探索型、存在探索型、結論探索型。
【關鍵詞】初中數學;解題策略;探索性問題;創造性思維能力
所謂探索性問題,是指在指定條件下尚不明確的結論、或由給出的結論探求滿足該結論所需要的條件的一類問題。探索性問題是開放性問題中的一種,其特點在于問題條件或結論不直接給出,需要解題者充分利用已知條件進行觀察、猜想、分析、歸納、推理,或探索不明確的結論,或尋找各種可能使問題成立的條件,或發現問題中所隱含的定理、公式、規律等。開放探索性題重在開發思維,促進創新,有利于培養學生的探索能力,而且還提供了創造性思維空間,是近年來數學問題中的熱點問題。此類問題雖背景新穎,不拘泥于常規解法,但對于近幾年中考出現的此類題還是有一定規律可循的。以下將介紹幾類探索性題目及其常用的解題策略。
一、條件探索型
題目中由問題給定的結論去尋找待補充或完善的條件,常用“當滿足什么條件時,能得到相應結論”的語句,解題時需執果索因,其解法類似于分析法,在結論成立的條件下,逐步探索其成立條件。它改變了傳統的思維模式,開拓學生的逆向思維,并能提高分析問題的能力。一般解題策略:執果索因,假設有了相應結論,再通過嚴密推理尋找使結論成立的條件。
例1:如圖(1)在等邊△ABC中,D、F分別為BC、AB上的點,且CD=BF,以AD為邊作等邊△ADE。(1)求證:△ACD≌△CBF;(2)探究:當點D在線段BC上何處時,四邊形CDEF是平行四邊形,且∠DEF=30°。分析:(1)由邊角邊公里不難證明;(2)當點D為線段BC中點時,由∠DEF=30°,延長EF交AD于點M,則點M為AD中點,在 CDEF 中,EM∥DC,則F也為AB邊中點,即BF=1/2·AB,而BF﹦CD,∴CD﹦1/2·BC,故當點D為BC邊中點時滿足題目條件。
二、 存在探索型
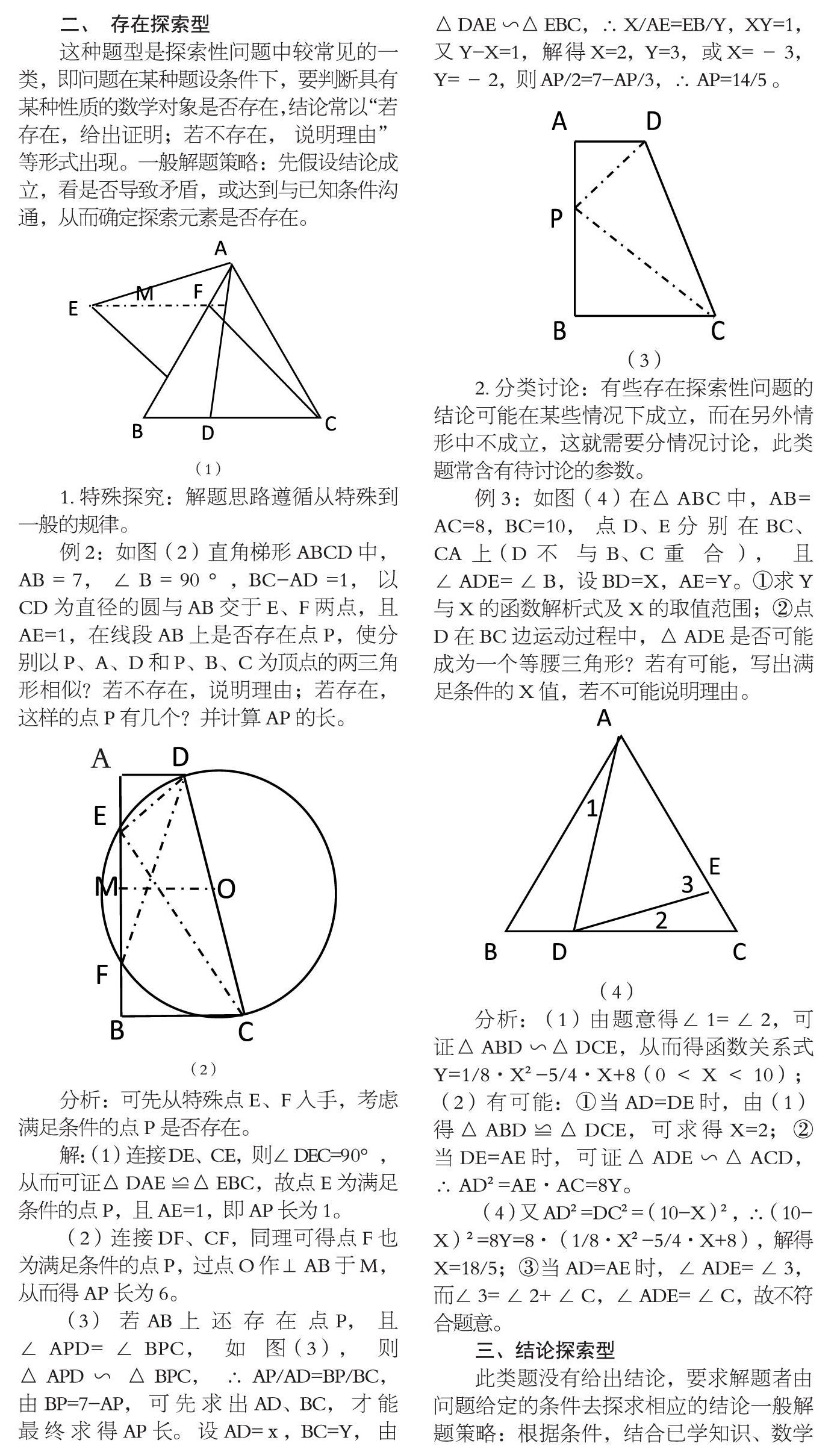
這種題型是探索性問題中較常見的一類,即問題在某種題設條件下,要判斷具有某種性質的數學對象是否存在,結論常以“若存在,給出證明;若不存在, 說明理由”等形式出現。一般解題策略:先假設結論成立,看是否導致矛盾,或達到與已知條件溝通,從而確定探索元素是否存在。
三、結論探索型
此類題沒有給出結論,要求解題者由問題給定的條件去探求相應的結論一般解題策略:根據條件,結合已學知識、數學思想方法,通過分析、歸納逐步得出結論。
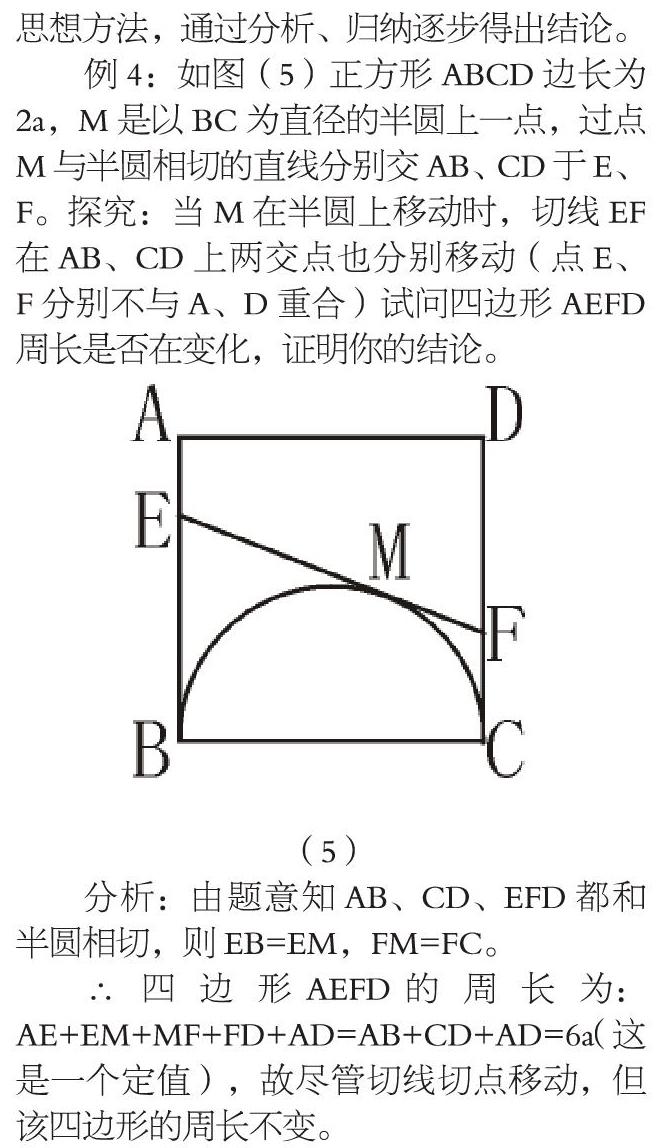
例4:如圖(5)正方形ABCD邊長為2a,M是以BC為直徑的半圓上一點,過點M與半圓相切的直線分別交AB、CD于E、F。探究:當M在半圓上移動時,切線EF在AB、CD上兩交點也分別移動(點E、F分別不與A、D重合)試問四邊形AEFD周長是否在變化,證明你的結論。
分析:由題意知AB、CD、EFD都和半圓相切,則EB=EM,FM=FC。
∴四邊形AEFD的周長為:AE+EM+MF+FD+AD=AB+CD+AD=6a(這是一個定值),故盡管切線切點移動,但該四邊形的周長不變。
此題在解答過程中運用切線長定理,把四邊形AEFD的邊長EF轉化為EB與FC之和,從而得到周長為定值。在探索某個值變與不變的問題時,有時不能直接得出結論,通常可取特殊情況(如上題取EF∥BC),先得結論,再設法證明。以上粗略介紹了幾類常見的探索性題及一般解題策略。
最后談幾點解此類題該注意的問題:1.認真審題,理解題意,盡可能地把題目涉及到的有關概念、性質、定理、公式、方法等都弄清楚,從而獲得最佳解題途徑;2.挖掘題目隱含條件,提高解題正確性,做到判斷正確,運算合理;3.開闊思路,這類題型要因題而定法,在充分分析命題特點的基礎上,聯想并利用與之相關的性質等,盡可能把問題轉化為熟悉、簡單的情形來處理。
參考文獻:
[1]趙桂麗.初中數學中探索性問題的研究[J].數理化學習(初中版),2006.
[2]馮敬文.初中數學教學中如何培養學生問題意識的對策探討[J].科技展望,2016(06):224.
[3]王金枝.淺談初中數學問題意識的培養[J].中國培訓,2015(08):169.
[4]任慧東.初中數學教學中培養學生問題意識的策略研究[J].讀與寫(教育教學刊),2012(09):80.

