基于核心素養的初中數學數形結合教學探究

朱西杰

摘要：隨著核心素養這一概念的深入探究，國內的很多的學者也逐漸提出了一系列培養學生核心素養的方法，為教師教學提供了先進的理念。對即將升入高中的初三生來說，學習上的壓力加劇了學生在學習上的困難，很多學生想要努力學習，但是又找不到正確的學習方法，逐漸失去了對學習的興趣。在初中數學的科目上，老師們需要不斷的提高學生核心素養，讓學生利用正確的方法來學習。

關鍵詞：核心素養;初中數學;數形結合;探究

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）04-109-2

在初中數學的教學過程中，老師可以通過數形結合的方法幫助學生學習數學。為了提高學生們的數學思維，學會利用傳統的數形結合的方法來解決數學問題，提高學生們的學習能力，老師們就要利用好數形結合的方法來進行教學，促進學生進一步理解數學知識，幫助學生解決數學問題。進一步提高初三學生們數學核心素養。

一、數形結合的概念和對強化核心素養的重要作用

數形結合作為數學老師教學時經常使用的方法，不僅能夠讓學生更加直觀的觀察圖形，學習數學知識，還能方便老師教學，闡述數學思路。這種方法將數值和圖形有效的結合在一起，能夠讓數學問題變得更加簡單、方便。

數形結合作為傳統的數學教學方法在教學效果上的顯示出了巨大的力量，很多學生在這樣的教學方式下更加了解數學知識，久而久之，學生們可以利用這種方法來自主的進行學習，進行數學問題的探究。老師在講解數學知識的時候，通過數形結合的方法將數學問題簡單化，也會減少學生們學習數學知識時的畏難情緒，進一步提高學生們學習的積極性，讓學生們的學習能力有所提高。

數形結合思想是中考必考的題目，也是學生必須掌握的核心素養之一。在每一年的中考中都會出現，也是學生感到困難的地方。從數到形，從文字語言和圖形語言的互譯，對學生的知識綜合和能力形成，思維訓練都非常有幫助。

二、基于核心素養的初中數學數形結合教學策略

1.增強導入的趣味性

都說良好的開端是成功的一半，好的課堂導入也會為數學課堂的成功展開“增光添彩”，增強課堂導入的趣味性能夠更好的吸引學生們學習的興趣，保證下一步的教學順利展開。老師們在實際的教學中可以通過數形結合的方式進行課堂的導入，通過幽默的語言和動作讓學生們直觀的感受在數學圖形的幫助下有效的解決數學問題。

比如，老師在帶領學生學習“二次函數的圖像和性質”的時候，為了增加課堂的趣味性，老師就要讓自己的課堂導入充滿趣味，讓學生對接下來的數學學習充滿期待。老師可以借助多媒體，通過白板，Forclass，幾何畫板，平板等教學手段讓學生在圖形結合的方法學習二次函數的圖形和性質。為了進一步了解二次函數，老師還可以對比一次函數和二次函數的區別，讓學生更加了解二次函數的性質。在導入環節，老師要注意語氣，以輕松、幽默的方式讓學生們學習和思考，幫助學生理解二次函數的相關概念。

2.利用數形結合理解數學難題

老師要想全面提升學生們的核心素養，就必須要采取適合學生們的學習方法，讓學生利用數形結合來解決數學問題。數學問題的解決就是應該讓學生利用簡單的方法來解決數學難題，這樣學生們的大腦思維才能得到有效的開發。但是很多老師為了讓學生提高分數，利用題海戰術，通過大量的刷題，讓學生們來理解數學難題。但是授之以魚不如授之以漁，學生終究還是要學會自己解決問題。所以，為了讓學生們更好的學習數學知識，參透數學問題的奧妙，老師要讓學生學會利用數形結合的方法，用總結數學問題和類型代替大量刷題，減輕學生的學習壓力。這樣，學生們才能更好的參與進來，提升自己學習數學的自信心，增強學習的主動性，學會主動思考和解決數學問題。數全面，形直觀，只有數，學生可能理解困難，對數量關系找不到，對問題沒法解決，只有形，學生對問題的全面掌握不足，只有數形結合，才可以對學生的解決問題產生幫助，從而提高學生學習的興趣，獲得成功的滿足感，促進學生學習。

圖形中的點，線段，圖形的位置，形狀都是對題目中文字語音的補充，也是隱藏的條件，沒有圖形，很多題就沒法解決。當然。沒有文字語言的描述，我們對圖形也不能有清楚的認識，只有數形結合，才是解決問題的捷徑。

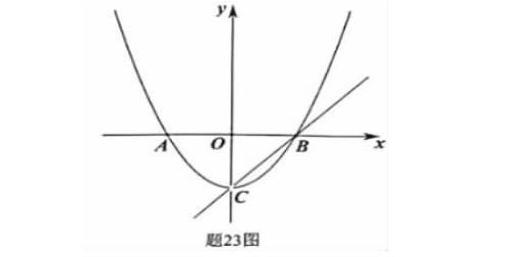
例如：廣東省2018年中考第23題是函數小綜合，直線與二次函數的結合，以求解析式與點的坐標形式入手，主要涉及到待定系數法列方程求函數解析式，一次函數與二次函數的交點問題，三角函數的定義，分類討論思想，今年本題增加了對存在性問題的探索，考查了考生的探究能力，與幾何知識的結合更緊密，對數形結合的能力提出了更高的要求。

題23.如圖，已知頂點為C（0，-3）的拋物線y=ax2+b（a≠0）與x軸交于A，B兩點，直線y=x+m過頂點C和點B.

（1）求m的值;

（2）求函數y=ax2+b（a≠0）的解析式

（3）拋物線上是否存在M點，使得∠MCB=15°？

若存在，求出點M的坐標;若不存在，請說明理由.

本題第三問在文字敘述中很難找到解決的途徑，但在圖形中畫一個∠MCB=15°，就很容易15°轉化為含有30°、60°角的直角三角形問題。對這種特殊的直角三角形的三邊關系的練習，是學生掌握比較好的，從而解決了這個問題。這就是數形結合思想在幫助解決問題的一個很好的例題。

3.重視學生在課堂上的主體地位

在傳統的教學方式下，學生在學習上很容易對老師產生依賴感，在學習方法上和解題思路上也很容易受老師教學方式的影響，老師們為了在有限的教學時間內完成教學任務，不知不覺的就省去了學生討論和課堂表現的教學環節。再加上老師的備課過分關注教材內容，忽視學生們的個人情感和學習的效果，使學生們的學習效果大大折扣，除此之外，在這種情況下，還容易產生“一言堂”的現象，使數學課堂成為了數學老師一個人的課堂，學生們只能作為被動的學習者來參與數學課堂。這樣不僅會影響學生們的學習效果，也會阻礙學生們數學核心素養的進一步發展。

為了改善這種情況，初三數學老師要重視學生在課堂上的主體地位，讓初三的學生在有效的教學方法下學會數學，讓初中生對自己的中考更有信心。初三數學老師作為學生中考路上的引路人，一定要要充分的發揮課堂的作用，讓學生們學會利用數形結合打開思維，發現解決問題的道路，通過小組討論和多種解決思路的課堂講解，讓學生進一步開發自己的大腦，促進核心素養的全面提高。

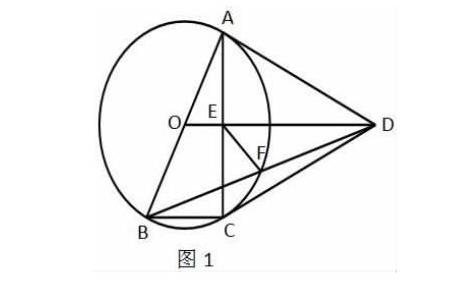
例如;廣東省2018年中考第24題：

如圖1，四邊形ABCD中，AB=AD=CD，以AB為直徑的⊙O經過點C，連接AC、OD交于點E

（1）證明：OD//BC;

（2）若tan∠ABC=2，證明：DA與⊙O相切;

（3）在（2）的條件下，連接BD交⊙O于點F，連接EF，若BC=1，求EF的長.

本題是圓的綜合問題。考查的內容有：三角形的全等，三角形的相似，平行的判定，中位線定理，垂徑定理，切線

的證明，勾股定理以及線段長度的計算。本題條件復雜，難度大，很多學生做不出，但利用數形結合的思想就非常容易。據有關老師統計，本題第（3）問有非17種解法。為什么有這么多解法哪？關鍵就在于：（1）F所在的位置比較特殊，F既是等腰直角△ABD斜邊上的中點，又是等腰直角△CEM斜邊上的中點。（2）圖1中，除了EF，其他線段的長度都較容易求得.這相當于多了很多已知條件.運用不同的線段組合，再加上不同的輔助線，便產生了各種各樣的方法.這就是典型的數形結合。 在對本題教學中，要小組討論，反復引導，歸納總結，利用數形結合的方法，引導學生積極思考，抽象出基本圖形，基本方法，督促學生養成主動學習，積極思考的習慣，在學習中發揮學生的主體作用，促進課堂教學的成效。使學生形成良好的數學素養。

綜上所述，基于核心素養的初中數學數形結合的教學不僅需要初三數學老師轉變教學方法、教學內容和教學模式，也需要讓學生學會利用數學解題的技巧來解決數學問題，培養學生們數學學科的核心素養，讓初三生能夠更有信心，充滿希望的面對即將到來的中考。

[參考文獻]

[1]章建躍.核心素養統領下的數學教育變革[J].數學通報，2017（04）.

[2]陳德燕.數學核心素養理念下的立體幾何教學——以“直線與平面垂直的性質”為例[J].數學通報，2017（02）

[3]胡松.以“數學素養”導引數學活動——《幾何圖形》教學實錄與思考[J].數學通報，2017（01）.

（作者單位：廣東省珠海市紫荊中學桃園路校區，廣東 珠海 519000）