精準滲透，有效提升兒童“類比”推理能力

林彩蓮

【摘? 要】? 邏輯推理能力是小學數學關鍵能力之一。本文闡述了其中的類比推理的基本內涵，并結合具體例子，談談如何找準滲透點，在小學數學不同教學領域中有效滲透“類比”推理，從而逐步發展學生的數學推理能力。

【關鍵詞】? 小學數學教學;滲透;類比推理

所謂類比，是從特殊到特殊的推理方法，就是在兩個或兩類事物間進行對比，找出若干相同或相似點后，推測在其他方面也可能存在相同或相似之處，并做出某種判斷的推理模式，稱為類比推理（簡稱類比）。在小學數學教學中，教師如果能夠找準滲透點，恰當地把新知識與舊知識進行“類比”，就可以實現有效的遷移，能用它求得一條通向已經解決的問題的通道，更重要的是可以幫助學生積累數學思考的經驗，使其養成一個有效的思考習慣，逐漸聰明起來。那么“類比”思想在小學數學教學中有哪些可以滲透的載體呢？

一、在公式的推導過程中滲透“類比”推理

在教學小學數學的平面圖形面積和立體圖形體積公式的推導時，教師往往通過把一個新問題拋給學生，讓學生憑借已有的知識經驗，通過轉化、類比，在舊知識的基礎上生長，學生就能自然完成新知識的自我構建。

【教學片段】

1.觀察類比，歸納方法

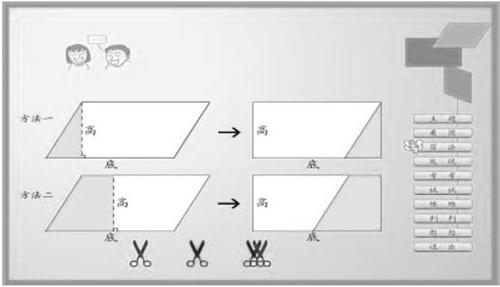
師：同學們把平行四邊形轉化成長方形，在操作時有一個共同點，是什么呢？（沿著平行四邊形的一條高剪開）

2.課件演示，認同方法

是不是任意一個平行四邊形都能轉化成一個長方形呢？教師用課件展示兩種剪法的過程。

3.合情推理，得出公式

討論：既然可以把一個平行四邊形轉化成一個長方形，那么平行四邊形究竟和長方形有怎樣的聯系呢？

匯報：隨著學生的回答課件同步展示兩種剪法，分別閃動相應的長與底、寬與高及小標尺度量的過程。

然后教師指名讓學生完整地說說平行四邊形的面積計算公式與長方形的面積計算公式的關系，并用字母表示公式。

以上是人教版《義務教育教科書·數學》五年級上冊第六單元編排的“平行四邊形的面積”的教學片斷。在學生動手把平行四邊形轉化成長方形的基礎上，教師通過課件同步演示，在驗證學生的操作過程中使學生體會到正確操作方法的重要性，積累操作經驗的同時能使學生再次體驗平行四邊形與長方形面積的關系，找到兩種圖形的相似點，把平行四邊形的面積與長方形的面積進行類比，為推導平行四邊形面積的計算公式提供正確的指向。

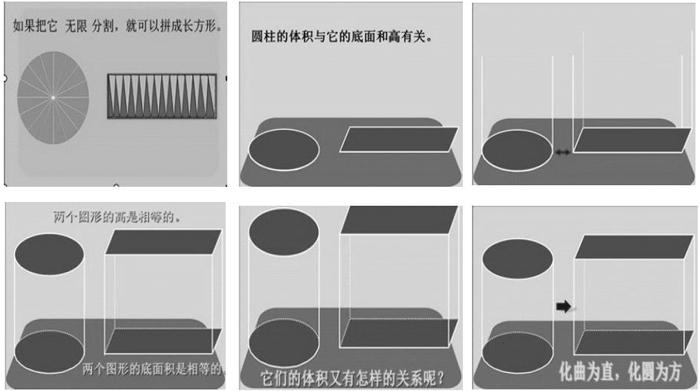
類似地，在教學“圓柱的體積”時，教師可以通過低維空間類比高維空間，即把平面圖形的知識類推到立體圖形的知識，讓學生受到啟發，深刻體會一個聯想的過程。（如下圖）

由圓柱的底面——圓，通過切割、拼合的方法，可以轉化成近似的長方形，如果把它無限分割就可以拼成長方形。如果把這兩個面同時往上平移相同的高度，所形成的不就是圓柱和長方體嗎？那它們又有什么相同之處呢？教師要引導學生明白：長方體的底面是由圓剪拼而成的，它們的面積是相等的;同時往上平移了相同的高度，因此它們的高也是相等的。于是，教師適時引導學生提出質疑：那么它們的體積又有著怎樣的關系呢？在這個過程中，教師利用圖形的變換，以舊引新，從面到體，滲透了類比、歸納、轉化和極限的數學思想，讓學生感受到圓柱與長方體似乎存在著某種聯系。這個時候，學生可能會合情地猜想：它們的體積是相等的，既然我們采用化曲為直、化圓為方的方法探究出了圓面積的計算公式，現在能否用類似的方法把圓柱轉化成長方體進行探究呢？這就有效地實現了類比思想的滲透。

類比推理不僅使數學知識容易理解，而且能使公式的記憶變得順水推舟般自然和簡潔，從而可以激發起學生的創造力，正如數學家波利亞所說：“我們應該討論一般化、特殊化和類比的這些過程本身，它們是獲得發現的偉大源泉。”

二、在關系的探索中滲透“類比”推理

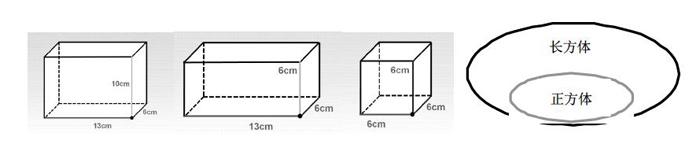
在人教版《義務教育教科書·數學》五年級下冊第三單元“長方體和正方體的認識”一課的教學中，教師可以在抽象出長方體的特征后，通過課件動態演示，將一般的長方體變成有兩個相對的面是正方形的長方體，再變成一個正方體（如下圖），然后引導學生通過觀察進行類比，發現它們的相同點，讓學生體會正方體具有長方體的所有特征，發現它的特殊性，形成“正方體是特殊的長方體”的結論，水到渠成地形成集合圖的關系。

三、在數學廣角的變式題教學中滲透“類比”推理

數學廣角可謂是數學思想方法滲透的搖籃。由于數學廣角中的變式習題的數學模型是隱藏的，給學生的思維帶來了很大的障礙，教學中教師需要引導學生進行聯想、尋找異同，從而實現學生對知識和方法的有效遷移。

“鴿巢問題”的變式問題有很多，應用更具靈活性。教師教學的關鍵是要引導學生把變式問題和“鴿巢問題”聯系起來，即弄明白把什么看做“待分物”，把什么看做“抽屜”，建立這兩者的數學模型，再利用例題中的方法解決該問題，讓學生在運用新知靈活巧妙地解決實際問題的過程中進一步體驗數學的價值，感受數學的魅力，培養學生的類比推理能力。

同樣，在教學“雞兔同籠”的變式題時，也需要運用“類比”的數學思想進行推理，建立解題模型。教師可以了解生活中的一些數學問題與“雞兔同籠”問題的聯系，讓學生說一說下面的題目哪些信息是表示總頭數，哪些信息代表雞數、兔數。

現在社會上常常批判同時開進水管、出水管等問題不切實際，這里的設計正是要學生體會數學來源于生活，又高于生活。雞兔可以同籠但并非生活中的常態，雞兔同籠問題其實是為了建立一類問題的數學模型，像練習中出現的車輪問題、購物問題、租船問題等，都可以由本課所學的列表法、配合二分法類比去解決。同時，變式練習既能鞏固學生的新知，又能發展學生抽象數學模型的能力和知識遷移能力。

四、對滲透類比推理教學的啟示

“知識本身并沒有力量，只有當我們用思維方法的杠桿去撬動知識解決問題時，才能實現知識的力量，達到智慧的生成”。類比推理，正是其中的“杠桿”之一。在小學數學教學中，如果教師能夠有意識地挖掘教材中蘊含類比推理思想的資源作為滲透點，并結合知識的特點和學生的認知規律，持之以恒地進行不同層次的滲透，就能逐步發展學生的類比推理能力，提高學生數學學習能力。

【參考文獻】

[1]義務教育數學課程標準[M].北京：北京師范大學出版社，2012.

[2]義務教育教科書·數學（四年級下冊）[M].北京：人民教育出版社，2012.