捕捉學(xué)生思維火花,提高課堂學(xué)習(xí)效果
安麗雅


[摘 ?要] 課堂是教學(xué)的主陣地,教師不僅要善于捕捉學(xué)生智慧的火花,發(fā)現(xiàn)、重組課堂教學(xué)中涌現(xiàn)出來的各種信息,把有價(jià)值的信息和問題進(jìn)行轉(zhuǎn)化,成為教學(xué)的閃光點(diǎn);還要在教學(xué)設(shè)計(jì)時(shí)調(diào)動(dòng)學(xué)生的積極性,讓學(xué)生主動(dòng)參與學(xué)習(xí)活動(dòng),敢于發(fā)表自己的想法和見解,從而提高他們的思維能力,從而達(dá)到知識(shí)的靈活運(yùn)用、觸類旁通的目的.
[關(guān)鍵詞] 初中數(shù)學(xué);思維火花;有效教學(xué)
新課程標(biāo)準(zhǔn)指出:數(shù)學(xué)教學(xué)活動(dòng),特別是課堂教學(xué)應(yīng)激發(fā)學(xué)生興趣,調(diào)動(dòng)學(xué)生的積極性,引發(fā)學(xué)生思考,鼓勵(lì)學(xué)生的創(chuàng)造性思維. 在現(xiàn)在的課堂教學(xué)中,教師不僅僅是一個(gè)知識(shí)的講解者,更重要的是學(xué)生學(xué)習(xí)活動(dòng)的組織者、引導(dǎo)者,以及信息的重組者. 教師不僅要善于捕捉學(xué)生智慧的火花,發(fā)現(xiàn)、重組課堂教學(xué)中涌現(xiàn)出來的各種信息,把有價(jià)值的信息和問題進(jìn)行轉(zhuǎn)化,成為教學(xué)的閃光點(diǎn);還要在教學(xué)設(shè)計(jì)時(shí)調(diào)動(dòng)學(xué)生的積極性,讓學(xué)生主動(dòng)參與學(xué)習(xí)活動(dòng),敢于發(fā)表自己的想法和見解,從而提高他們的思維能力,達(dá)到知識(shí)的靈活運(yùn)用、觸類旁通的目的.
教師在課堂上要善于捕捉學(xué)生的思維火花,因勢(shì)利導(dǎo),完善教學(xué)效果
在課堂教學(xué)過程中學(xué)生往往會(huì)有一些突發(fā)的靈感,甚至是一些錯(cuò)誤的理解,教師是按照自己的教學(xué)進(jìn)度繼續(xù)講下去,還是耐心地傾聽學(xué)生的想法?筆者想大部分教師會(huì)選擇后者. 因?yàn)槲覀冎缹W(xué)生才是課堂的主體,教師一味地講解,學(xué)生機(jī)械地記憶,教學(xué)效果會(huì)很差. 只有真正讓學(xué)生的思維動(dòng)起來,才能達(dá)到事半功倍的效果.
第一,利用“一題多解”,激發(fā)學(xué)生的創(chuàng)新思維,歸納總結(jié)選取最優(yōu)方案. 在一次試卷評(píng)講時(shí),有一道填空的壓軸題,當(dāng)時(shí)做出來的學(xué)生并不多,因?yàn)閳D形有兩次翻折,一看圖就覺得很難,很多學(xué)生就放棄了.
題目如下:如圖1,△ABE和△ACD是△ABC分別沿著AB,AC翻折180°形成的,若∠1 ∶ ∠2 ∶ ∠3=28 ∶ 5 ∶ 3,則∠α的度數(shù)為______.
本題考查圖形的折疊變化及三角形的內(nèi)角和定理,關(guān)鍵是要理解折疊是一種對(duì)稱變換. 根據(jù)軸對(duì)稱的性質(zhì),折疊前后圖形的形狀和大小不變,因此可以找到相等的角.
解:如圖1,設(shè)∠1=28x,∠2=5x,∠3=3x,由∠1+∠2+∠3=180°得28x+5x+3x=180°,解得x=5°,故∠1=28×5°=140°,∠2=5×5°=25°,∠3=3×5°=15°. 因?yàn)椤鰽BE和△ACD是△ABC分別沿著AB,AC邊翻折180°形成的,所以∠BAE=∠DAC=∠1=140°,所以∠DAE=140°×3-360°=60°,所以∠DAB=∠EAC=∠α=80°(根據(jù)“8字形”).
當(dāng)筆者按照自己的思路講完后,覺得大家都聽懂了,就準(zhǔn)備講下一題. 這時(shí)有一位學(xué)生舉手說出她有其他的方法:既然△ABE和△ACD是△ABC分別沿著AB,AC邊翻折180°形成的,那么BA,CA就是∠EBC和∠DCB的平分線. 如圖2,根據(jù)∠1=90°+∠BGC可得∠BGC=100°,則∠α=80°.同學(xué)們聽完后一個(gè)個(gè)都表示贊同,課堂里開始活躍了起來,從學(xué)生的表情上可以看得出來,這位學(xué)生的方法比筆者的簡(jiǎn)單. 筆者首先表揚(yáng)了這位積極發(fā)言的學(xué)生,并從她的解答中受到了啟發(fā)——還有更簡(jiǎn)單的方法!于是筆者鼓勵(lì)其他學(xué)生順著發(fā)言同學(xué)的思路繼續(xù)尋找更好的方法. 教室里從興奮到討論再到安靜,每個(gè)學(xué)生都希望一鳴驚人. 終于有人舉手了:因?yàn)锽A,CA是∠EBC和∠DCB的平分線,據(jù)外角定理得∠α=∠GBC+∠GCB=2∠2+2∠3=80°.此解法更佳!同學(xué)們不禁拍手叫好:為什么我們一開始沒有想到這個(gè)方法呢?于是筆者讓每個(gè)學(xué)生都反思一下,有的說復(fù)雜的圖形蒙蔽了我們的眼睛,應(yīng)該在復(fù)雜圖形中抽象出我們熟悉的基本圖形;有的說沒有把握軸對(duì)稱的性質(zhì),等等. 學(xué)生都表現(xiàn)得非常積極,這一次課堂上的意外反而激發(fā)了學(xué)生探究的熱情,學(xué)習(xí)效果顯而易見.
第二,對(duì)學(xué)生的思維火花給予正面的引導(dǎo)和鼓勵(lì),激發(fā)學(xué)生的學(xué)習(xí)興趣. 數(shù)學(xué)的課堂如果都是教師在講解,學(xué)生被動(dòng)接受,那么肯定是枯燥乏味,而且知識(shí)容易被遺忘. 怎樣才能讓一個(gè)定理或結(jié)論深深地印在學(xué)生的腦海里呢?
在上“負(fù)整數(shù)指數(shù)冪的運(yùn)算”這一課時(shí),已經(jīng)推導(dǎo)出了公式a-n= ,隨后給出一串小題讓學(xué)生利用該公式計(jì)算:-2=______,-3=______,-2=______. 大部分學(xué)生按照筆者的要求做完了,但一小部分學(xué)生開始嚷嚷,煩分?jǐn)?shù)化簡(jiǎn)計(jì)算量太大了,還容易計(jì)算錯(cuò). 筆者順勢(shì)提醒大家看看算出來的結(jié)論有什么特點(diǎn). 小陳同學(xué)眼睛一亮,因?yàn)?1=2,所以-2=?搖2=22=4,因此公式還可以寫為a-n==n. 回答得太漂亮了,這正是筆者所希望的. 為了表示對(duì)小陳同學(xué)的肯定,筆者模仿書上將這個(gè)公式命名為“陳某某公式”,小陳得意極了,其他學(xué)生也投來了羨慕的眼神. 以后每次用到這個(gè)公式,同學(xué)們都會(huì)大聲地說這是“陳某某公式”,我們班以學(xué)生的名字命名的公式和定理便越來越多,大家對(duì)這些定理都記憶猶新,大大地提高了課堂學(xué)習(xí)的效果. 因此鼓勵(lì)學(xué)生發(fā)表自己的獨(dú)特見解,讓他們?cè)趯W(xué)習(xí)中體驗(yàn)成就感,很大程度上能激發(fā)學(xué)生的學(xué)習(xí)興趣.
第三,巧妙利用學(xué)生的錯(cuò)誤想法,讓學(xué)生在錯(cuò)誤中反思. 蘇霍姆林斯基說過:“教育的技巧并不在于能預(yù)見到課的所有細(xì)節(jié),而在于根據(jù)當(dāng)時(shí)的具體情況,巧妙地在學(xué)生中不知不覺地做出相應(yīng)的變動(dòng). ”所以教師要利用課堂上的突發(fā)思維,甚至是學(xué)生的錯(cuò)誤想法轉(zhuǎn)化成課堂上寶貴的教學(xué)資源,成為同學(xué)們引以為戒的反例,能達(dá)到更好的教學(xué)效果. 例如,在學(xué)習(xí)同底數(shù)冪的除法時(shí),黑板上出了這樣一道題:-y3n+1÷yn+1. 小張學(xué)生不假思索地脫口而出:-y2n+2. 下面開始小聲議論,有小部分同學(xué)表示贊同,也有同學(xué)表示反對(duì). 其實(shí)這是一個(gè)典型的錯(cuò)誤,在以往的考試和作業(yè)中一直有同學(xué)犯類似的錯(cuò)誤,這是一個(gè)很好的“反面教材”啊. 筆者讓小張同學(xué)上黑板把他的運(yùn)算過程寫出來:原式=-y3n+1-n+1= -y2n+2. 同學(xué)們發(fā)現(xiàn)了他的錯(cuò)誤,減多項(xiàng)式整體的時(shí)候一定不能忘了加上括號(hào). 我們?cè)僖黄鸹仡櫫苏降募訙p的方法以及去括號(hào)的法則,并把這個(gè)錯(cuò)誤命名為“張某某錯(cuò)誤”,每個(gè)學(xué)生都對(duì)“張某某錯(cuò)誤”記憶深刻,大大減少了類似錯(cuò)誤的發(fā)生.
教師的備課要有彈性和開放性,為激發(fā)學(xué)生的思維火花創(chuàng)造條件
傳統(tǒng)的教學(xué)過分地強(qiáng)調(diào)預(yù)設(shè),也就是嚴(yán)格按照教案上課,課堂上要提哪些問題,包括有幾個(gè)環(huán)節(jié),每個(gè)環(huán)節(jié)要用多少時(shí)間都是精心計(jì)算好的. 所以往往有時(shí)開課的時(shí)候請(qǐng)學(xué)生討論也是規(guī)定時(shí)間的,不管學(xué)生有沒有討論出結(jié)果,或者學(xué)生有不同的理解,為了預(yù)設(shè)的時(shí)間,就匆匆進(jìn)入下一個(gè)環(huán)節(jié). 這樣缺乏對(duì)學(xué)生好奇心的激勵(lì),缺乏學(xué)生對(duì)問題的鉆研,久而久之,學(xué)生就會(huì)失去學(xué)習(xí)數(shù)學(xué)的興趣了,所以備課要留有余地. 當(dāng)課堂上出現(xiàn)學(xué)生了不同的見解或突發(fā)情況,要給學(xué)生充分的思考時(shí)間,把一個(gè)問題研究透徹,鼓勵(lì)學(xué)生表達(dá)、糾錯(cuò),讓學(xué)生的思維真正活躍起來,往往能收到意想不到的效果.
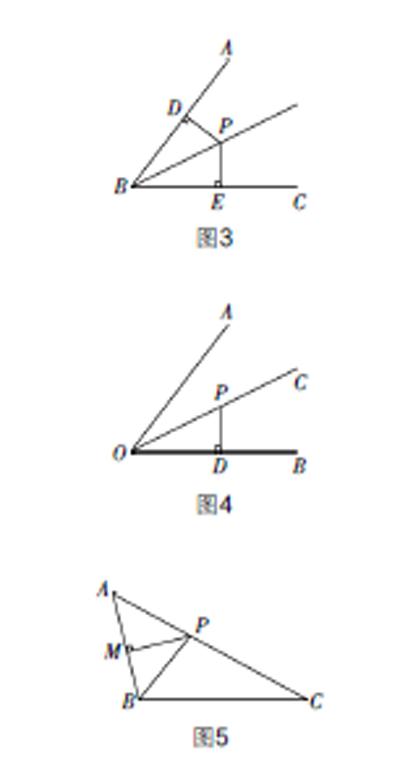
第一,教師在課前要根據(jù)班級(jí)學(xué)生的特點(diǎn)做好充分的準(zhǔn)備,要預(yù)見到不同層次學(xué)生的基礎(chǔ)以及學(xué)習(xí)該知識(shí)點(diǎn)的困難所在,激發(fā)高水平的精彩的生成. 例如,在“角的軸對(duì)稱性”的復(fù)習(xí)課時(shí),筆者把由易到難的幾道題串起來進(jìn)行講解,收到了不錯(cuò)的效果. 第一步,如圖3,先復(fù)習(xí)角平分線的性質(zhì)和幾何語言的書寫;第二步,直接利用性質(zhì)解決一道基礎(chǔ)題,求點(diǎn)P到OB的距離,如圖4,并引出常見的輔助線的添法;第三步,如圖5,BP為△ABC的角平分線,已知AB,BC的長(zhǎng)度直接寫出△ABP與△BPC面積的比值;第四步,如圖6,已知AC平分∠BAD,判斷∠ABC與∠ADC的數(shù)量關(guān)系. 前三題大部分學(xué)生都能很快回答出來,但在第四題上出現(xiàn)了百家爭(zhēng)鳴的景象,有的學(xué)生受到教師前三題的影響,添出了點(diǎn)C到AB,AD的距離(如圖7),也有學(xué)生采用了前一章學(xué)習(xí)的“截長(zhǎng)補(bǔ)短”證全等的方法(如圖8、圖9)解決了問題. 課堂上學(xué)生積極發(fā)言,思維活躍. 當(dāng)最后一?搖題題目出現(xiàn)時(shí),學(xué)生個(gè)個(gè)躍躍欲試,都想爭(zhēng)做“解題達(dá)人”. 題目是:如圖10,分別以△ABC的邊AB,AC為邊向外作等邊三角形ABD和ACE,CD與BE相交于點(diǎn)O,判斷∠AOD和∠AOE的數(shù)量關(guān)系并證明. 雖然第四題的圖形復(fù)雜,但是有了上面題目的啟發(fā),還是有不少學(xué)生成功地添出了輔助線(如圖11),獲得了成功的體驗(yàn). 解題完成以后要讓學(xué)生歸納總結(jié)一下添輔助線的技巧,歸根到底是要構(gòu)造軸對(duì)稱圖形,這樣有利于幫助學(xué)生克服對(duì)難題的恐懼,激發(fā)學(xué)生探索求知的欲望,達(dá)到解決一類題目的目的.
第二,課堂上要留給學(xué)生足夠思考、討論的時(shí)間,教師是課堂教學(xué)的引導(dǎo)者,學(xué)生才是課堂教學(xué)的主體,教師不能替代學(xué)生發(fā)現(xiàn)問題,而應(yīng)該創(chuàng)設(shè)情境引導(dǎo)學(xué)生發(fā)現(xiàn)、歸納結(jié)論,激發(fā)學(xué)生的創(chuàng)新思維. 在上一次函數(shù)的應(yīng)用時(shí),大多數(shù)情況都是教師給出題目由學(xué)生解答. 為了拓展學(xué)生的思維,筆者從學(xué)生熟悉的小故事入手,將題目改為開放式的問題,學(xué)生一下子就來了興趣,通過小組PK,比一比哪個(gè)組得到的信息最多,哪個(gè)小組得到的信息最有價(jià)值,哪個(gè)小組得到的信息最有難度. 如圖12,“龜兔賽跑”是同學(xué)們熟悉的寓言故事,圖中表示了路程s(m)與時(shí)間t(min)之間的函數(shù)關(guān)系, 請(qǐng)同學(xué)們仔細(xì)看圖,你能從圖中獲取哪些信息?學(xué)生們聯(lián)系實(shí)際,積極思考,得到了很多精彩的答案,大家不僅掌握了一次函數(shù)的性質(zhì),還對(duì)一次函數(shù)的應(yīng)用留下了深刻的印象.
第三,課堂教學(xué)是師生雙邊活動(dòng)的過程,教學(xué)活動(dòng)的成效在很大程度上取決于師生融洽的程度、了解的程度,教師對(duì)學(xué)生的影響、學(xué)生之間的合作與競(jìng)爭(zhēng)、班級(jí)的學(xué)習(xí)風(fēng)氣都會(huì)對(duì)課堂教學(xué)產(chǎn)生不容忽視的影響. 良好的課堂學(xué)習(xí)氛圍,教師一個(gè)鼓勵(lì)的眼神,一句表揚(yáng),一個(gè)提醒,都是學(xué)生學(xué)習(xí)的動(dòng)力和源泉. 只有讓課堂“活”起來,呈現(xiàn)出生機(jī)勃勃的精神狀態(tài),才能激發(fā)學(xué)生的思維火花,提高學(xué)生的創(chuàng)新能力,從而提升課堂學(xué)習(xí)的效率.
總之,高質(zhì)量、高效率的課堂教學(xué)是促進(jìn)學(xué)生有效學(xué)習(xí)的前提,課堂教學(xué)目的在于使每一位學(xué)生不斷地獲得新知識(shí)和能力,使每一位學(xué)生獲得最大的進(jìn)步和發(fā)展. 新課程改革提倡向45分鐘要效益,這就要求我們每一位教師要立足課堂,以學(xué)生為本,實(shí)施促進(jìn)學(xué)生有效學(xué)習(xí)的教學(xué)策略,探索促進(jìn)學(xué)生有效學(xué)習(xí)的教學(xué)模式,充分調(diào)動(dòng)學(xué)生的學(xué)習(xí)積極性,激發(fā)學(xué)生求知探索的欲望,真正地愛上數(shù)學(xué)、愛上學(xué)習(xí).

