淺析從學生錯題中優化學生的數學思維的策略

摘?要：數學老師遇到同樣的問題是：學生作業上出現的問題老師講評過了幾遍，還是有些學生會出錯，幾乎班上每個學生都發生過。學生的錯題有兩種情況，一種是學習不夠認真，隨便應付老師和家長的錯誤，另一種是有一定數學基礎的但數學思維比較僵化的錯誤。對于學習態度不夠認真的學生來說，出現的一些錯題利用課堂來講評，課后有針對性來補是可以撿起來的;對于數學有一定基礎的學生出現錯題來說，基本上是數學思維上存在著的問題，所以優化學生的數學思維是非常重要的，也是數學老師一直都在努力重點探討的問題。

關鍵詞：錯題;數學思維;興趣

數學是一門邏輯性很強的學科，它需要學生要有很好的思維能力，而思維是打開數學的鑰匙。有了良好的數學思維能力，就能夠提高去分析問題，解決問題的能力。特別對初中學生來說，他們已有一定認知能力和接受能力，在平時的教學中適當地滲透數學思維是非常必要的，而從學生錯題中是尋找問題的關鍵，更能有針對性地進行學生的數學思維的優化。本文就從三個方面淺析從學生錯題中優化學生的數學思維能力。

一、 熟悉各種數學模型和背景，形成學生數學思維的依據性

現在都提倡數學來源于生活，服務于生活，它不是平白無故地冒出來，是有一定的前提條件和背景的。新課標中對數學課程標準中有要求學生會建立數學模型“從學生已有的經驗中出發，讓學生親身經歷將實際問題抽象成數學模型并進行解析與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態度和價值觀方面得到進步和發展”。數學模型常見的有方程模型、不等式模型、函數模型、幾何模型、統計概率模型等等。從七八九年級的學生錯題中，發現應用題錯誤率較高，學生怕做，思維亂，不懂從文字題里讀取信息，不知從何下手，找不到解決問題的突破口，這也反饋學生對于各種數學模型和背景的不熟悉，缺乏思維的依據性，也就無從下手了。

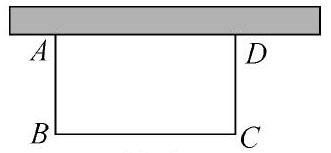
如圖，用一段長為40m的籬笆圍成一個一邊靠墻的矩形花圃ABCD，墻長28m。設AB長為xm，矩形的面積為ym2。

1. 寫出y與x的函數關系式;

2. 當AB長為多少米時，所圍成的花圃面積最大？最大值是多少？

3. 當花圃的面積為150m2時，AB長為多少米？

此題的數學模型是函數模型，根據長方形的面積公式去建立等量關系式，但要注意它的背景條件是用一段長為40m的籬笆圍成一個一邊靠墻的矩形，就要確定兩個條件一是矩形的邊長AD不需要用籬笆去圍，另一是注意這段長只有40m，其中x是受限制的，因此得

知道了數學模型，還要了解和熟悉它的背景條件，像我們初中數學中經常碰到求最值問題，就要熟悉最值的幾種模型有垂線段最短、兩點之間線段最短、函數中的最值等等，同時也要熟悉它的背景條件，給學生提供解決問題的依據。這也就要求教師在平時數學教學中，就要不定時地給學生介紹各種數學模型，讓學生有意識地了解和記住它們，有條件的話還能結合實際創造背景條件，也就是采用變式，讓學生更深層次去理解和運用，思維能觸類旁通。熟悉了各種數學模型和背景，學生的思維就有了依據，思維就能活躍，一看到此類題目，就能聯想到要用什么知識去解決。

二、 訓練各種數學語言轉化能力，促進學生數學思維的條理性

數學語言包括數學符號語言、文字語言、圖形語言，它承載著數學知識、思維和思想，是學生學好數學的重要組成部分。從學生的錯題中，出現各種數學語言轉化的卡殼，也就對數學知識不能更好地理解，從而出現錯題或講評完重做還是錯。數學題型有的很單一，很明了地告訴學生直接用什么知識就可以解決的，但大部分題型還需轉彎費些功夫才可以解決，這就需要各種數學語言轉化，讓抽象的具體化、形象化、直觀化，讓枯燥的生動化、簡明化、條理化。在初中數學教學中，教師就應引導學生分析，理解題設給出的數學語言，去尋找解題的思路和方法。

（一）培養數學符號意識

小學的數學出現更多的是具體的數，而在初中，從七年級開始各種數學符號就慢慢呈現出來了，最常見的是用字母代表數，如果一些概念性質定理只單一地用文字描述叫學生去記，去理解，學生做題的錯誤率非常高，學生不理解題目里出現的符號，經常問“這是什么鬼”“這個題目有錯”等等。

例如，七年級數學上冊，學完了絕對值中有一習題，若|x|=x，問x的范圍，它就是“任何一個有理數的絕對值是非負數”也就是“|x|≥0”絕對值的性質運用，很快就得到x≥0;再如已知a+b=0，其中a，b≠0問-ab的符號，這就是需要學生明白“a，b兩個互為相反數”的符號語言就是“a+b=0”，反過來“a+b=0”就是“a，b兩個互為相反數”，由于a，b≠0，a，b兩個數中必有一正一負，異號相乘ab的積為負，-ab就為正了。學生明白了這些數學符號言就不會出現思路亂，沒條理，還分類討論弄出好幾種答案的錯誤結論。

學習數學的人，就必須掌握數學符號語言，它簡單明了，理解它就少走彎路，直奔主題。

（二）培養數形結合意識

數形結合的思想是學習數學的重要思想方法之一，它體現的是圖形語言，它能使抽象的問題形象化、直觀化，使復雜的問題簡單化，它解決了數學中的邏輯性和條理性，使學生更易理解數學知識，這種思想方法出現的數學題型在八九年級的數學學習中滲透得越來越多。

用y=m這條平行x軸的直線從下往上移，直觀可以看到，在圖A中兩者無交點，繼續往上移到圖B位置兩者有一個交點，移到圖C位置有兩個交點，繼續往上移都有兩個交點，因此就可以判定y=m要在y=-2的上方就滿足條件，所以m>-2。

在我們平時教學中要引導學生數化形的思想，很多抽象不好理解的題目，通過借助于圖形的直觀形象的特點，加深學生對知識的理解、記憶，加強學生解題的數學思維，從而找到解題的思路。

三、 合理設計和構造問題，提高學生數學思維的方向性

數學問題有簡單的、有復雜的、有綜合性強的、有思維靈活的等等，而每一種都有它設計的用意。同一類題型，看似相同，但從不同角度來設計的話，思考問題的方向就有所改變，這對于一般的學生來說，是不會區別的，一概而論。從學生的錯題中反饋的比較明顯，沒有區別度，寫出的答案很單一，要么走進死胡同，繞不出來。

因此，在平時的數學教學中，選例和變式都要有目的地進行創造條件，求同存異，引導學生當條件發生變化時，就要認真審題，特別強調思考此題的方向是否要改變，就不能想當然，同理可得了，有時還需要進行合理構造成熟悉的知識來解決，明確了解題的思維方向，才能更好地去優化學生的思維能力。

面對著現在著力提倡“壯腰”工程，而初中生就處于“腰”這一階段，如何去讓“腰”這一階段變得強大起來，壯實起來，從數學這一學科來說，我的想法是先從學生的錯題入手，尋找解決問題辦法，了解學生錯的原因，有針對性地優化學生的數學思維。以上就是我從學生錯題中對學生學習數學的思維進行優化的幾點策略。

四、 總結

總之，學好數學的關鍵就是要有良好的數學思維，在我們的數學課堂中，就要善于抓住學生在課堂中暴露的問題或課后的作業出現的問題進行有效的教學，引導和培養學生自發領悟、自我分析問題和解決問題的能力，從而達到思維能力的優化，提高學生的數學成績。

參考文獻：

[1]趙蓸榮.巧用數學語言?激活數學思維[J].高中數學教與學，2015，326（1）：3-4.

作者簡介：

黃旭萍，福建省三明市，福建省三明市第十中學。