大道至簡，規避討論

王曉

[摘? 要] 分類討論是解析數學問題十分常用的方法，但解析過程中對學生的分類能力、討論思維有著較高的要求. 在實際解題時可以采用一定的策略方法來合理規避分類討論，提高解題效率. 文章結合實例深入探討數形結合、函數性質、分離參數、變換主元四種規避策略，提出相應建議.

[關鍵詞] 規避;分類討論;數形結合;函數;參數;主元

分類討論是高中數學重要的解題思想和方法策略，可將復雜的問題拆分為若干個基本問題，解析時需分為“分類”和“討論”兩個過程，但對學生的解析思維有著較高的要求. 若分類的標準確定有誤，很容易造成討論的過程不完善，勢必會造成解題錯誤. 從解法優化角度來看，在解題時若能轉化思維角度或采用解題策略來簡化甚至規避分類討論，則可以提升解題效率，下面對規避策略加以探究.

滲透數形結合，規避分類討論

數形結合在求解函數問題中有著廣泛的應用，實際上該方法策略也可用于規避分類討論，即求解某些代數類問題時，可以構造對應的函數，并繪制函數圖像，利用函數圖像的直觀性來解題.該規避策略常用于涉及含參函數、方程、不等式等問題中.

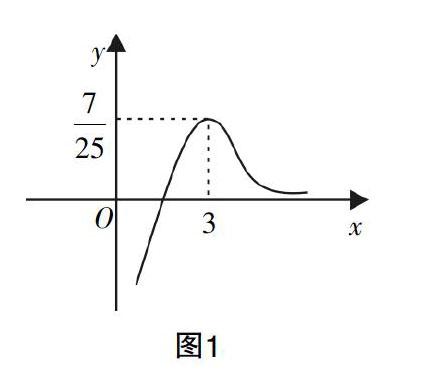
例1：ax3-x2+x+1=0是關于x的方程，已知該方程在（0，+∞）上的實數解有且僅有一個，試求實數a的取值范圍.

分析：題干所給方程是一個含有參數a的關于x的一元三次方程，無法直接獲得其解，常規解法是對a的取值范圍加以討論. 此時我們就可以采用數形結合的方法，基于方程構建相應的函數，通過研究函數的圖像與x軸的交點個數來確定實數a的取值范圍.

解：可將原方程變形為--=a，可設f（x）= --=（x>0），則f（x）的導函數為f′（x）=-. 分析可知在（0，3）上，函數f（x）單調遞增，在（3，+∞）上單調遞減，又可求得f（3）=>0，f（1）=-1，在（3，+∞）上f（x）>0. 從而可以繪制圖1所示的圖像，由圖可知當a=或a≤0時函數與x軸有唯一的交點，即對應的方程在（0，+∞）上的實數解有且僅有一個，因此實數a的取值范圍為aa=，a≤0 .

總結與指導：數形結合規避分類討論的最大優勢是圖像直觀，可以直接獲得解題突破的關鍵信息. 但在學習時需要掌握解讀函數圖像的方法，能夠從函數圖像中提煉出曲線交點、變化趨勢，值域、定義域，以及曲線之間的相對位置等內容，并能夠用關系式來表示.

活用函數性質，規避分類討論

函數性質在分析取值類問題中有著廣泛的應用，對于一些涉及變量討論的取值問題，則可以充分利用函數的性質來加以簡化，規避討論. 例如常用的函數對稱性、單調性等. 一般利用函數性質來規避分類討論時，需要根據題干性質提取原函數的關鍵性質，并用函數關系或不等式來具體化，逐步將問題轉化為相應的方程組或不等式組.

例2：對于函數f（x），其在定義域[-1，1]上是偶函數，并且在區間[0，1]上單調遞增，已知f（1+m）

分析：題干給出了函數f（x）的性質及單調區間，需要根據函數間的不等關系來求m的取值范圍，常規的做法是討論函數的定義域，確定每個區間上的情形，但該方法相對較為煩瑣，此時就可以利用該函數的對稱性來規避分類討論. 函數f（x）是偶函數，則必然滿足f（x）=f（-x）=f（x），后續只需要利用該對稱性質來加以分析即可.

解：f（x）在定義域[-1，1]上是偶函數，則根據偶函數圖像的對稱性可知該函數滿足f（x）=f（-x）=f（x），從而可將不等式轉化為f（1+m）

總結與指導：函數性質是函數內容學習的重點，利用函數性質可以解決多類型問題，例如方程、不等式等問題. 而在學習時需要關注函數構建的方法，建立函數與方程、不等式之間的關系，掌握問題轉化的技巧與思路.

合理分離參數，規避分類討論

參數取值的不確定性是造成分類討論的原因之一，因此在分析某些函數取值問題時，則可以考慮采用分離參數法，通過將參數與函數分離的方式來規避討論. 在求解時首先對函數的參數進行分離，等價轉化問題，一般將其轉化為相應的不等式問題或函數取值問題，然后利用相關性質來對其取值加以分析.

例3：已知函數f（x）=-ax（x>0且x≠1），如果存在x∈[e，e2]使得f（x）≤成立，試求實數a的取值范圍.

分析：函數f（x）內含有參數a，討論特定條件下關于函數的不等式成立，而a的取值不確定，常規思路是設定分類標準，討論對應條件下不等式成立的情形. 但該種思路相對較為煩瑣，可以采用分離參數的方式，將參數a集中到不等式的一邊，轉化為函數的最值問題.

解：存在x∈[e，e2]，使得f（x）≤成立，代入函數解析式，則有-ax≤，可將其變形為a≥-，則需要分析-的值域，可以構建函數g（x）=-，其中x∈[e，e2]，則有a≥g（x）min. 通過分析g（x）的導函數可以確定函數g（x）在區間[e，e2]上單調遞減，則g（x）min=g（e2）=-，即a≥-，所以實數a的取值范圍為

總結與指導：分離參數是重要的數學方法，從表面上來看是將參數轉移到符號的一側，實際上是為了方便構建函數，利用函數的性質回避討論. 需要注意的是在分離參數時要嚴格按照數學運算法變式，關注參數對應的取值.

靈活變換主元，規避分類討論

對于某些含參不等式問題，如果從常規的角度來設定主元求解，有時需要對參數的取值加以討論，其過程較為復雜，此時可以考慮采用變換主元的方法，即設定參數為不等式的主元，然后分析參數與未知數之間的變化，并借助相應的函數知識來對參數的取值加以討論，從而獲得最終答案.

例4：已知不等式mx2-2x-m+1<0，對于滿足m≤2的一些m均成立，試求x的取值范圍.

分析：上述為含參不等式，表面上是關于x的一元二次不等式，需要討論滿足成立條件下的m的取值. 為避免分類討論則可以采用變換主元的策略，即將不等式視為是關于m的一元一次不等式，則對應的解集就為[-2，2]，求x的取值范圍，可以通過分析參數m與x的變化來完成.

解：根據不等式來設定函數，設f（m）=（x2-1）m+（1-2x），可將其設為是關于m的一次函數，對應的圖像就為一條直線，根據題意可知當m∈[-2，2]時，直線位于y軸的下方，因此需要滿足的條件為f（-2）<0，f（2）<0，可得不等式組-2x2-2x+3<0，2x2-2x-1<0，可解得

總結與指導：變換主元實際上是變換問題視角，在主元變換的過程中需要嚴格遵循函數、方程、不等式的設定要求. 在學習時需要引導學生關注知識本質，引導學生多角度看待問題，拓展解題視野.

解后深度反思，思考教學建議

分類討論可以促進問題的條理性，但思維過程較為煩瑣，需要確保討論過程不“重”不“漏”，這也是在解析問題時要合理規避分類討論的原因所在. 上述是對規避分類討論四種策略的實例探究，下面基于突破過程提出兩點建議.

建議1：關注問題轉化的過程

從上述四種策略來看，規避分類討論實際上就是轉化問題視角，將對應問題轉化為分析過程較為簡潔的問題，例如轉化為函數問題、不等式問題等. 因此在學習時需要關注問題轉化的策略，學習知識之間的關聯，如利用函數值域來分析不等式、方程取值. 一般問題轉化時可以按照如下步驟進行：首先確定問題類型，思考對應的知識關聯，結合知識聯系點對問題等價轉化，然后利用等價問題的性質定理來探究結論.

建議2：關注規避策略的思想

解題過程中所用的方法策略背后隱含的是數學思想，因此實際上就是在數學思想的指導下完成了思路構建，例如上述對問題轉化就是化歸轉化思想的應用體現，而數形結合分析問題的過程中滲透著數形結合思想. 因此學習分類討論的規避策略就需要立足對應數學思想，掌握數學思想的本質內涵，深刻理解思想方法解析問題的精髓所在. 數學思想與知識定理同等重要，在探究運用過程中可以提升自我的思維品質，因此在教學中需要教師重點引導，合理滲透.

總之，規避分類討論的策略有很多，上述只是其中四種較為常用的，而規避過程實際上就是問題轉化過程，該過程中需要學生深刻理解問題，破除思維定式，充分利用關聯知識來合理轉化. 而轉化解題同樣可以鍛煉思維，因此對提升思維能力有著極大的幫助.