設計真實的探究活動　提升學生數學核心素養

欒長偉

摘要：自中共中央、國務院發布《關于深化教育教學改革全面提高義務教育質量的意見》，提出落實 “五育”并舉，實現立德樹人以來，基層數學教師在不斷嘗試如何將德育元素融入數學課堂。這樣的探究也與落實《中國學生發展核心素養》目標下對于數學核心素養發展的探究是一致的。在課堂上，要設計能引發學生生疑的問題情境和真實可靠的探究過程，我們可以通過設計能引發學生生疑的問題情境，設計“真實可靠”的探究過程，來實現全面落實立德樹人、全面提升學生的數學核心素養的目標。

關鍵詞：探究過程;核心素養;立德樹人

中共中央、國務院發布的《關于深化教育教學改革全面提高義務教育質量的意見》，其核心內容是落實“五育”并舉，實現立德樹人。《中國學生發展核心素養》也對探究學生的數學核心素養指明了方向。當前的課堂中，設計能引發學生生疑的問題情境，設計真實可靠的探究過程是落實上述目標的重要環節。然而，仍有很多教師忽略了探究過程所帶給學生的探究價值。實際上，要想讓學生明白知識的形成過程，教師就要設計科學合理、深度通透的知識探究過程。

一、設計能引發學生生疑的問題情境

數學是促進學生思維發展的核心學科之一。問題情境是現實生活與數學學習之間、具體問題與抽象概念之間的橋梁。它的價值不僅僅是激發學生的興趣，更應該讓學生通過情境建立新舊知識之間的聯系并在具體情境中發現問題，進而提出質疑，從而為課堂重點來作鋪墊。通常的問題情境創設有如下兩種形式。

一是從“數學知識內部”引入。其更多趨近于“復習式引入”，是為了建立新舊知識之間聯系的渠道，在學生已有知識的基礎上，在學生的“最近發展區”內設置既能引發學生回憶，又能對新知識產生好奇心的問題情境。例如，在教學人教版《義務教育教科書·數學》七年級上冊“直線、射線、線段”時，可以在前一節課的“點動成線”的基礎上，設計動畫效果，從屏幕的外部飛入一個點，再從屏幕中飛走，形成的路線即是直線，直線上的兩個點即可以表示為直線AB，射線、線段與其類似。

二是從“生活實際問題”引入。這樣一方面容易激發學生對現實生活中數學價值的探求欲，同時也能讓學生體會到數學不是孤零零的、沒有溫度的，而是來源于生活，貼近于生活的。例如，在教學人教版《義務教育教科書·數學》八年級上冊“整式乘法”中，教材設計的問題2為：光的速度約是3×105km/s，太陽光照射到地球上的時間是5×102s，你知道地球和太陽之間的距離是多少嗎？這一問題既是學生現實生活中的問題，又能讓學生產生強烈的好奇心，同時，還有較高的教學探究價值。另一方面，很多實際問題的設計更能凸顯數學文化，其實也就是賦予數學教學一種人文情懷。在數學教學過程中，每講到一個定理，其背后往往都存在一個故事、一個趣聞、一段歷史或一些體會，這就會使枯燥的定理和公式有了鮮活的色彩和生動的形象，學生記憶起來會更加深刻。

二、設計“真實可靠”的探究過程

探究過程實際上是為了給學生提供一個親身經歷知識形成過程的機會，并在學生親自感悟的基礎上，進行突出數學品質、提煉數學思想方法的引導，這樣才能將知識內化成能力。

例如，在“兩點確定一條直線”時，《義務教育數學課程標準（2011年版）》稱為“基本事實”，不再稱為“公理”。人教版教材上提出的問題是“用幾個釘子可以固定一根木條”，從而讓學生發現“基本事實”是來自于生活的，這樣就具有較好的情境設計意義。事實上，在課堂實踐中，教師常用可以粘貼的“紙條”來代替“木條”在黑板上演示。我的想法是“木條要盡量細一些，要盡量趨近于直線”。同時，當將“紙條”撤下后，要用粉筆將撤下的紙條畫成“直線”，將固定紙條用的磁鐵石畫成“點”，而這個過程就是數學中的抽象過程，是數學的核心思想，是學生從實際生活過渡到數學問題的有效途徑。

也有的教師設計了這樣的探究問題：過一個點可以畫幾條直線？過兩個點呢？如此，相當于直接從數學問題出發，如果能繼續追問“過不共線的三個點呢”就會有錦上添花之妙。通過“不同個數的點畫直線”都會得到同樣一個結論，學生才會從內心 “承認”，“過兩點可以畫一條而且只可以畫一條直線”。

再如，在教學人教版《義務教育教科書·數學》八年級上冊“平方差公式”一課時，教材設計了如下問題：計算下列多項式的積，你能發現什么規律？（1）（x+1）（x-1）=______;（2）（m+2）（m-2）=______;（3）（2x+1）（2x-1）=______。

此情境的創設有兩個缺點，一是每個多項式的第二項均是數字，所以才會有學生總結說“一個單項式與一個數字的和乘以這個多項式與這個數字的差”;另一個缺點是所有的兩個多項式都滿足“兩數和與兩數差的積”的形式，這對于學生歸納能力的培養是存在不足的。歸納結構的前提是對已有結構的分類，所以要在問題中加入不滿足平方差條件的形式。如，（3x+2）（3x-4）=_______;（2x-y）（3x+3y）_______。然后，可以追問：“等號左邊的哪幾個多項式具有共同特點？他們積有什么特點？”

從實際課堂的總結中可以發現，關于平方差的描述，學生會總結出兩種規律，一是“兩個數的和乘以這兩個數的差等于這兩個數的平方差”，即平方差公式;另一種是“同號兩項的積與異號兩項的積的和”，這是課堂上學生真實的總結，是建立“真實可靠”的探究過程所得到的學生自然生成。在此基礎上，讓學生再舉出滿足結構的多項式乘積，驗證自己的猜想是否正確，這才是從特殊歸納出一般，再回到特殊的思維過程。

最后是關于用幾何圖形驗證平方差公式的過程，很多教師不理解為什么要用圖形驗證。實際上，圖形的驗證過程是一種“數形結合”的方法體現，也是在后期學習中，例如“勾股定理”探究的一種方法鋪墊。教材中圖形設計的意圖很明顯（如圖1）。

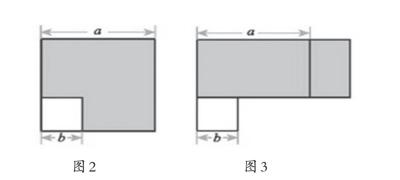
此圖可以看成是邊長為a的正方形減去邊長為b的正方形，再將剩下的①部分拼接到②位置，得到變成為（a+b）的正方形;或者理解為長為（a+b），寬為（a-b）的長方形的長邊上截取寬為b，長為（a-b）的長方形（即②），并將其拼接到①位置。相比之下，從學生的課堂的認知反應來看，北師版教材中關于平方差公式的驗證更符合學生的認知規律（如圖2和圖3及例題）。

例題：如圖2，邊長為a的大正方形中有一個邊長為b的小正方形。

（1）請表示圖2中陰影部分的面積。

（2）小穎將陰影部分拼成了一個長方形（如圖3），這個長方形的長和寬分別是多少？你能表示出它的面積嗎？

（3）比較（1）和（2）的結果，你能驗證平方差公式嗎？

就是說，將兩個圖形分開，看起來會相對更清晰一些。在圖2的提示下，我們可以嘗試設計更加開放的問題探究：

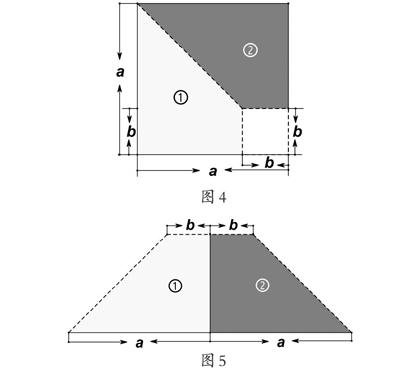
師：有的同學將邊長為a的正方形剪掉一個邊長為b的正方形，將剩下部分按虛線裁剪成①和②兩部分（如圖4），并將這兩部分分別拼成梯形（如圖5）和平行四邊形（如圖6），請你借助圖5和圖6完成平方差公式的證明。

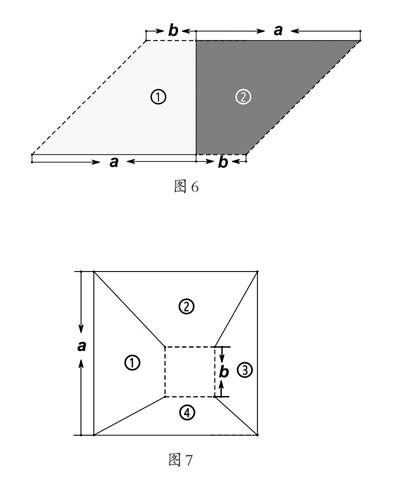
師：有的同學在邊長為a 的正方形的內部剪掉一個邊長為b的正方形（如圖7），你能用兩種方法表示①②③④部分面積和嗎？

經過以上完整的驗證過程，學生經歷了從整式乘法的計算尋找共同規律，從而猜想出平方差公式，再用文字和符號兩種語言進行描述，最后通過圖形設計開放性的面積驗證策略，這是探究的實際價值。學生得到的不僅僅是一個廣為應用的平方差公式，更是以后進行命題探究的基本方式。

基于核心素養的初中數學課堂，教師應該堅守以人為本的教育理念，圍繞數學核心知識，通過創設恰當的問題情境，提出有效的數學問題，開展適度的深度探究。應引導學生自主地學、聯系地學、批判地學、通透地學，進而在知識與技能形成的中，在情感與態度升華中，在思想與經驗的積累過程中培養學生的數學核心素養。

參考文獻：

[1]張坤英.初中數學教學過程中學生核心素養培養途徑探析[J].中國校外教育，2019（11）.

[2]馬莉瑩.核心素養視角下初中數學課堂教學研究[J].中國課程資源，2019（10）.

（責任編輯：楊強）