淺析基于核心素養培育的小學數學教學
陳展群
摘 要:培育、發展學生的核心素養是我國全面深化課程改革、推進落實立德樹人根本教育任務的重要環節。具體到學科建設及知識教授方面,核心素養的內涵和外延存在較大差異,需要面向教學內容、教育對象展開具體分析。文章抓取具體案例,結合“核心素養”的相關特質展開教學研究,致力探索出科學合理的教學范式。
關鍵詞:小學數學;核心素養;教學實踐;三角形三邊關系
中圖分類號:G623.5 文獻標識碼:A 收稿日期:2019-11-20 文章編號:1674-120X(2020)15-0072-02
一、基于核心素養培育的小學數學教學論述
到目前為止,關于小學數學核心素養的界定,教育理論界及實務界并沒有形成統一的標準,一些專家學者倡導從小學數學“四基”出發,而很多一線教師注重從小學數學教學內容的“四大模塊”出發。
對應差異化的理論、實踐認知區域,各種觀點主張均有可行之處,但又存在一定的瑕疵。例如,從以理論為主導的“四基”出發,需要小學數學學科重新根據“四基”定義核心素養的內涵,不僅周期冗長且難保障不同區域小學數學教育的適應性;而從以實踐為主導的“四大模塊”出發,則需要對小學數學各模塊教學內容的外延進行“收攏”,保障其符合“核心素養”的基本特征,但又無法在較大范圍內保障實效性。據此,小學數學教師可轉換一種思維,即借鑒已經成熟的核心素養培養機制,將其轉化為適合小學數學教學使用的教學范式。
從宏觀角度出發,《中國學生發展核心素養》給出了明確的定義:“核心素養是指學生應具備的,能夠適應終身發展和社會發展需要的必備品格和關鍵能力。”小學數學教師可從中提煉出兩個基本界定標準:其一,是“終身發展”;其二,是“社會發展”。前者的要求對應小學生當前個人能力,后者的要求對應小學生在當前社會生活中的數學實踐能力。
從微觀角度看,《普通高中數學課程標準(2017年版)》中給出了“核心素養”的限定范圍,包括“數學抽象”“邏輯推理”“數學建模”“直觀想象”“數學運算”“數據分析”六種。這六種“核心素養”都符合宏觀角度下“社會發展”的需要,但對“終身學習”不能一概而論,因為“終身學習”是有階段性的,在小學階段培養學生的核心素養必須契合“該階段”下終身發展的適應性。通過分析,“邏輯推理”“數學建模”“數據分析”三項過于超前,不適合在小學數學教學中作為“核心素養”培育的部分。
二、基于核心素養培養的“三角形的三邊關系”課例教學范式
綜合以上論述分析,基于核心素養培育的小學數學教學可按照“數學抽象”“直觀現象”“數學運算”展開,這一思路借鑒了高中數學“核心素養”的成熟模式,因此不需要對三種“核心素養”內涵、外延的可行性進行深度論證,有利于具體教學實踐活動的開展。其中,“數學抽象”是數學學科的基本特征,《義務教育數學課程標準(2011年版)》(以下簡稱《數學標準》)中明確指出,“數學作為對客觀現象抽象概括而逐漸形成的科學語言與工具”。因此,無論教學哪一方面的數學知識點,都要考慮其“數學抽象”的素養。而“直觀現象”素養培育比較符合小學生心理發育特點,該階段學生大多為6~12歲,按照兒童認知發展理論分析,恰好處于“具體運算階段”(Concrete Operations Stage),其思維特征表現為“守恒性、可逆性、去中心性”,盡管事物認知能力上離不開具象支持,但抽象思維日漸強化。最后,“數學運算”是小學數學教學的主要內容,縱觀整個小學階段知識點及知識點的相互聯系,都是建立在“數字”“運算法則”之上的。基于以上三種核心素養培育的“三角形的三邊關系”課例教學如下。
(一)基于數學抽象的教學范式
數學抽象是建立在數學具象表達基礎上的,人教版小學數學四年級下冊“三角形的三邊關系”知識提供了一系列“具象表達”的內容(參考P63-3),教師可以充分利用教材案例展開“數學抽象”核心素養的教學范式構建。以“小明選哪條路上學距離最短?”作為問題,引導學生將具體圖例表達轉化成抽象符號表達。(如下圖所示)
結合教材內容,教師將小明家用A點替代,郵局用B點替代,商店用C點替代,學校用D點替代。這種簡易繪圖的方式,不僅可以將現實生活中的事物形象“抽象化”(將曲線變成直線),同時也簡化了學生的思考過程,因此,由小明家到學校的路程問題,就可轉化成“線段AD”是否是最短的問題。主要教學案例部分如下。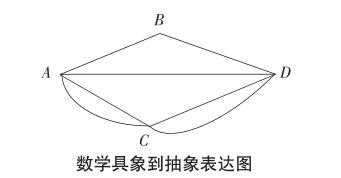
師:(結合實際圖片)同學們,請幫助小明同學觀察一下,哪一條路最近?如果是你,會選擇怎么走呢?
生:(根據自己的觀點作答)
教學預設1:選擇“小明家—郵局—學校”路線;要求學生說明理由,部分學生認為雖然有兩段路,但每一段路都很短,相比中間較長的路,走起來更近。
教學預設2:選擇“小明家—商店—學校”路線;要求學生說明理由,部分學生認為曲線的路要比直線的路短。
師:看來同學們的意見不統一,請跟老師一起,把小明上學的路線簡化一下,這樣我們可以看得更清楚。
(出示數學具象到抽象表達圖)
師:我們已經知道了,兩個點之間直線的距離是最短的,那么請同學們先對比一下,線段“AC+CD”和曲線“AC+CD”哪個距離更短呢?
生:線段最短。
師:既然如此,我們就可以排除曲線的干擾了,這樣小明家到學校之間的距離問題,就變成了兩個三角形的問題,其中A點、B點、D點連接起來就構成了一個三角形,A點、C點、D點連接起來又構成了另一個三角形。
生:對。
師:下面問題就簡單了,我們拿出直尺量一下,看三條路哪條路最短?
通過測量和多次實踐,學生能夠深刻認識到“三角形兩邊之和大于第三邊”的特征。因此,基于“數學抽象”核心素養培育的小學數學教學,主要是引導學生學會排除干擾、無效要素,將自然語言(圖文)的表述形式轉化成純粹的“數學語言”。例如,本案例中將小明家、學校等轉化成具體的A點、D點,學生掌握這種思維之后,也能夠用數學抽象思維來思考現實生活中的問題,從而提高數學應用能力。
(二)基于直觀想象的教學范式
有關“直觀想象”核心素養的解讀,主要是針對空間、集合、關系等數學知識內容而言的,據此構建小學數學教學范式,重點在于規律的總結。以“三角形的三邊關系”教學為例,教師可事先準備一批“小木棒”,上面標注各自的長度,統一分發給學生,(可采用分組方式)讓學生嘗試用三個小木棒圍成一個三角形。在學生多次嘗試后,讓學生匯報情況,將能夠圍成三角形的長度組合歸納成一組,將不能圍成三角形的長度組合歸納成一組。接著,進入“直觀想象”核心素養培養階段,教師利用多媒體設備出示一組“判斷表格”(如下表所示),讓學生自行判斷哪些能夠圍成三角形、哪些不能圍成三角形。這一過程中同樣需要學生動手參與,在學生給出答案之后,教師應立即讓學生動手驗證,以此增強其直觀體驗。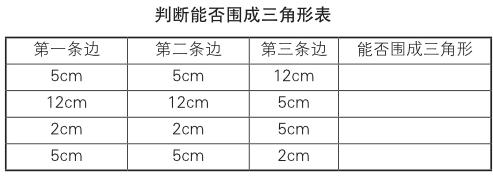
主要教學案例部分如下。
師:第一條邊和第二條邊都是5cm,第三條邊是12cm,能不能圍成三角形?
生:能/不能。
師:請同學們拿起手邊的小木棒,試一試。
生:不能。
師:第一條邊和第二條邊都是12cm,第三條邊是5cm,能不能圍成三角形?
生:能/不能。
師:請同學們拿起手邊的小木棒,試一試。
…………
基于“直觀想象”核心素養構建小學數學教學范式的過程中,“直觀”是必要條件。結合以上教學,學生會發現自己原本認為“可圍成三角形”的組合形式,卻不能在現實中實現,而教師在這一方面可以表現出“先知”的優勢,吸引學生去主動驗證“兩邊和大于第三邊”的結論是否正確。
(三)基于數學運算的教學范式
數學運算素養旨在培養學生的科學精神,并讓學生在這一過程中掌握正確的處理手段、演繹手法、推理工具,整體上可視為數學邏輯思維的“進階培養”。
以“三角形的三邊關系教學”為例,采用“數學運算”核心素養培養構建數學范式,應該說是一種最簡單、最有效的策略。但它的過程相對枯燥,教師要酌情運用,筆者更傾向于將其作為“驗證機制”,即在學生已經明白“兩邊和大于第三邊”的特征之后,給學生提供相關數據或“三角形”,讓學生判斷是否成立。例如,教師可以拋出這樣一個有爭議性的問題:“是不是所有的三角形的兩邊和,都會大于第三邊?”這樣就可以廣泛運用數據運算形式去驗證,其本質屬于“以數解形”。
三、結語
綜上所述,數學是我國學校教育視域下的“主課”之一,也是社會科學、自然科學等諸多領域的重要工具。而在當前《數學課程標準》中尚未明確“核心素養”內涵、外延的情況下,外部借鑒需要遵循適應性、實用性原則,本文基于小學數學“三角形的三邊關系”案例,對“數學抽象”“數學運算”“直觀想象”三類核心素養的價值進行了驗證,可作為小學數學課堂教學范式構建的依據。
參考文獻:
[1]袁喜云.小學數學教學中學生核心素養的培育[J].中國教師,2019(S1):35.
[2]史麗娟.小學數學教學中學生學科核心素養的有效培育[J].西部素質教育,2019,5(6):97.

