借助聯想法 打開數學解題思路

黃振東

摘 要：高中數學解題中借助聯想法，能很快地找到解題思路，提高學習效率.因此教學中應為學生講解聯想法的相關理論，并借助具體例題為學生講解聯想法的具體應用，給其解答類似問題帶來良好的啟發，促進其解題能力的顯著提升.

關鍵詞：高中數學;解題思路;聯想法

所謂聯想指由一事物想到另一事物的思維過程，主要包括相似聯想、對比聯想、接近聯想等.高中數學教學中為使學生能夠靈活運用聯想法解答相關題，應做好例題的精講，使學生親身體會不同聯想法的具體應用，把握聯想法的應用細節，徹底掌握最重要的解題方法.

一、運用相似聯想解題

相似聯想是指在性質或形式上相似的事物之間所形成的聯想.運用相似聯想解題時應引導學生積極回顧相似的知識點或知識的推導過程，根據題干通過聯想以往所學，迅速找到解題的突破口.教學實踐表明，相似聯想常應用在數列習題解題中，用于解答有關數列的新定義題，因此教學中應注重篩選并為學生講解相關的例題，提高學生運用相似聯想解題的意識與能力.

該題目為新定義題，很多學生遇到新定義題往往不知所措.事實上，解題時運用相似聯想可柳暗花明.認真審題可知，題干創設的情景與等比數列較為類似，因此可聯想已學過的等比數列通項公式的推導方法，尋找等積數列項與項之間的規律.

二、運用對比聯想解題

對比聯想是指在具有相反或相對立性質的事物間所形成的聯想.當從正面解答數學問題較為繁瑣，難度較大時，可運用對比聯想從其反面入手進行解答.使用對比聯想解答相關習題時，往往能獲得事半功倍的良好效果，因此教學中為提高學生對比聯想解題的意識與能力，既要注重講解相關的例題，又要組織學生開展相關的專題訓練活動，使學生能夠準確地找到問題的反面，為其正確解題奠定堅實基礎.

例2 若函數f（x）=lnx+ax2-2在區間（12，2）內存在單調遞增區間，則a的取值范圍為.

解答該題時如采用直接法需要考慮很多種情況，解答較為繁瑣，而且容易出錯.為提高解題效率，可運用對比聯想從其反面思考，即“函數f（x）在區間（12，2）內存在單調遞增區間”的反面為在該區間恒遞減，求出a的取值范圍后，取其反面即為要求解的結果.對函數求導得到f ′（x）=1x+2ax=2ax2+1x.令g（x）=2ax2+1，接下來需要進行分類討論：當a>0時，在區間（12，2）上g（x）>0，不符合題意，舍去;當a=0時，仍不符合題意，舍去;當a<0時，只需滿足g（12）=a2+1≤0，即，a≤-2，因此，滿足題意的a的取值范圍為（-2，+∞）.

三、運用接近聯想解題

接近聯想是指接近的事物之間形成的聯想.如看到函數問題可聯想到函數的單調性、奇偶性、周期性以及函數圖象等內容.接近聯想是學生在解題中應用率較高的一種聯想法.教學中為使學生熟練運用接近聯想解答相關習題，教學中應注重設計相關的問題，給予學生啟發，使學生能夠迅速的聯想接近的知識點.同時，優選經典的例題，并在課堂上為學生深入的剖析，使學生能夠找到接近聯想的切入點，盡快地找到解題思路.

該題是函數零點問題，遇到函數問題可使用接近聯想進行求解，聯想函數圖象借助函數圖象進行分析解答.

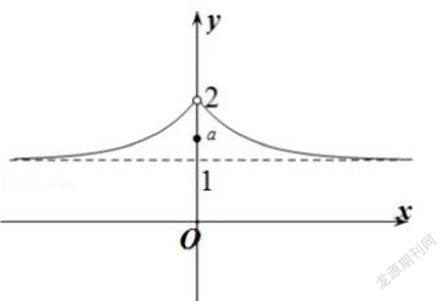
根據題干繪制出函數f（x）的圖象，如圖1所示：

令t=f（x），即，2t2-（2a+3）t+3a=0，解得t=a或t=32.①當a≤1或a≥2時，由圖1可知f（x）=a只有一個解x=0;f（x）=32有兩解，方程共有3個不同零點，不符合題意;②當a=32時，方程共有三個不同零點，不符合題意;③當1

綜上可知a的取值范圍為（1，32）∪（32，2），正確選項為D.

聯想法是一種解答數學問題的重要方法.高中數學教學中為使學生能夠靈活地應用，促進其解題能力與解題水平的顯著提升，應注重在課堂上為學生灌輸聯想法，提高學生對聯想法相關理論的認識與理解.同時，結合具體例題為學生逐一、認真講解不同聯想方法在解題中的應用，使其深入地體會應用過程，真正地能夠運用聯想法打開相關習題的解題思路.

參考文獻：

[1]薛玉.高中數學解題中聯想解題法初探[J].中國農村教育，2019（36）：109.

[2]姚玉敏.解析聯想方法在高中數學解題思路中的應用[J].讀與寫（教育教學刊），2019，16（12）：105.

[3]莊美榮.聯想方法在高中數學解題思路中的分析[J].華夏教師，2019（31）：36.

[責任編輯：李 璟]