以“靜”制“動(dòng)”

摘 要：中考數(shù)學(xué)試卷中經(jīng)常出現(xiàn)動(dòng)點(diǎn)問題.動(dòng)點(diǎn)問題可以以選擇、填空、解析等多種題型呈現(xiàn).學(xué)生面對動(dòng)點(diǎn)問題時(shí)，常常不知道如何下手.突破動(dòng)點(diǎn)問題這一教學(xué)難點(diǎn)成為初中數(shù)學(xué)教學(xué)的重要任務(wù).本文將初中數(shù)學(xué)中的動(dòng)點(diǎn)問題分為一條線段最值問題、兩條線段最值問題兩大類，進(jìn)行歸類分析，并提出教學(xué)建議.

關(guān)鍵詞：初中數(shù)學(xué);動(dòng)點(diǎn)問題;歸類分析

中圖分類號：G632 文獻(xiàn)標(biāo)識碼：A 文章編號：1008-0333（2020）11-0036-02

一、動(dòng)點(diǎn)問題歸類分析

1.一條線段最值問題

（1）單動(dòng)點(diǎn)問題

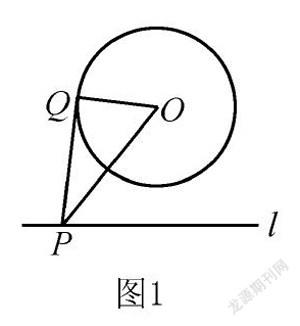
例題1 如圖1所示，存在一個(gè)圓O，已經(jīng)知道圓的半徑為2.存在一條直線l，圓心到l的距離為3.假如在直線l上有動(dòng)點(diǎn)P，PQ切圓O于Q點(diǎn)，則PQ的最小值是多少？

解析 根據(jù)題意可知，線PQ相切于圓O，OQ⊥PQ，∠OQP=90°，△OPQ為直角三角形.PQ的長度可以由OQ和OP計(jì)算出來.而OQ的值恒為2，OP取值越小，PQ取值也越小.當(dāng)OP⊥l時(shí)，OP最小.可以知道OP=3時(shí)PQ最小.對△OPQ運(yùn)用勾股定理得PQ=√（OP-OQ）=√5.

點(diǎn)評 本題是一道單動(dòng)點(diǎn)的一條線段最值問題，其難度不是太大，關(guān)鍵是學(xué)生能夠根據(jù)勾股定理分析出決定PQ最小值的線段OP何時(shí)最小.

（2）雙動(dòng)點(diǎn)問題

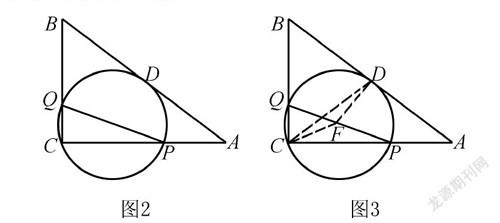
例題2 三角形△ABC三條邊分別為AB、AC和BC，它們的長度分別為10、8和6，動(dòng)圓經(jīng)過C點(diǎn)，它和AB邊相切，如圖2所示.已知?jiǎng)訄A與CA，CB相交于P、Q.請問PQ能夠取得的最小值為多少？

解析 AB、AC和BC長為10、8、6，滿足勾股定理，△ABC是直角三角形，∠C=90°.∠C=90°可以說明線PQ為圓F的直徑.假設(shè)點(diǎn)F是QP的中點(diǎn)，點(diǎn)D是圓F與線AB的切點(diǎn).因?yàn)閳AF和AB相切，有FD⊥AB.從圖中可以看出，F(xiàn)C+FD=PQ.在三角形FCD中，F(xiàn)C+FD>CD.從圖中可以看出，點(diǎn)F在△ABC高上時(shí)，CD能夠取到最小值，PQ也為最小值.使用面積法，得CD=BC·AC/AB=4.8.因而，線段PQ的最小值是4.8.

點(diǎn)評 本題是一道雙動(dòng)點(diǎn)的一條線段最值問題.因?yàn)閱栴}以動(dòng)態(tài)圓的形式出現(xiàn)，學(xué)生不易分析出線段PQ取最小值時(shí)的條件.在解決這道題時(shí)需要學(xué)生通過找圓心，繪制輔助線的方式來尋找突破口.

2.兩條線段最值問題

（1）單動(dòng)點(diǎn)問題

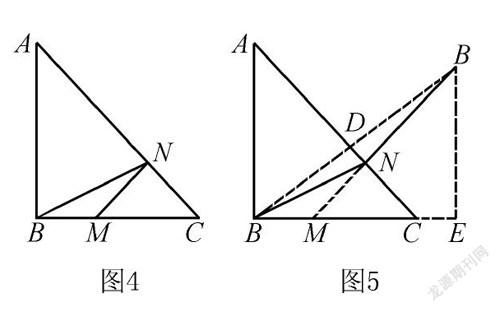
例題3 有一個(gè)直角三角形ABC，邊AB的長度和邊BC的長度相等，都等于4，∠B=90°.M是直角邊BC上的一個(gè)點(diǎn).已經(jīng)知道BM為1，N是AC上的動(dòng)點(diǎn).求BN和MN之和的最小值.

解析 作B關(guān)于AC的對稱點(diǎn)B′，并且連接MB′，過點(diǎn)B′作B′E，使B′E和BC垂直，如圖5所示.根據(jù)點(diǎn)B與B′的對稱關(guān)系，BB′⊥AC，BD=DB′.因?yàn)椤螦BC=90°，AB=BC=4，所以AC=√（AB+BC）=4√2.而BD=√（AB-AD）=2√2，則BB′=2BD=4√2，因而EB=EB′=4，ME=4-1=3.在Rt△MB′E中使用勾股定理，得到B′M=5.所以BN+MN的最小值是5.

點(diǎn)評 本題是一道單動(dòng)點(diǎn)的兩條線段的最值問題.在本題的解決過程中，使用到鏡像法，這是一種比較難以掌握的幾何技巧，需要學(xué)生對圖形有一定的感覺.因?yàn)椋瑢W(xué)生在解題時(shí)要具有鏡像法的應(yīng)用基本能力.

（2）雙動(dòng)點(diǎn)問題

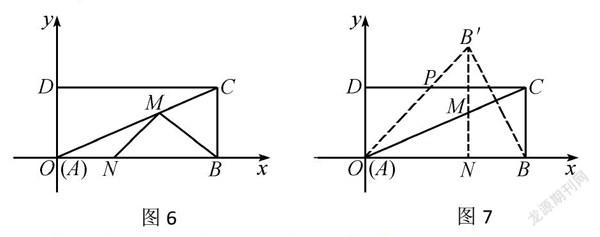
例題4 矩形 ABCD在一個(gè)平面直角坐標(biāo)系中，如圖6，矩形的頂點(diǎn) A、B、C 的坐標(biāo)是（0，0）、（20，0）、（20，10）.線段 AC上有動(dòng)點(diǎn)M，AB 上有動(dòng)點(diǎn) N.當(dāng) BM和MN和有最小值時(shí)，求點(diǎn) M 的坐標(biāo).

解析 作點(diǎn)B關(guān)于AC的對稱點(diǎn)B′，如圖7.過點(diǎn)B′作OB的垂線，垂線B′N與MC相交于M點(diǎn).從圖中可以看出，B′N=B′M+MN，則B′N=BM+MN.BM+MN的最小值等于B′N的長度.將O點(diǎn)B′點(diǎn)連接起來，和DC交于P點(diǎn).ABCD是一個(gè)矩形，則DC∥AB，有∠BAC=∠PCA.B和B’對稱，所以∠PAC=∠BAC，則∠PAC=∠PCA，所以PA=PC.現(xiàn)在令PA=x，則PC=x，而PD=20-x.在直角三角形ADP中，有PA=PD+AD，代入長度有x=（20-x）+10，解方程得x=12.5.因?yàn)閏os∠B′ON=cos∠OPD，所以O(shè)N∶OB′=DP∶OP，有ON∶20=7.5∶12.5，則ON=12.因?yàn)閠an∠MON=tan∠OCD，所以MN∶ON=OD∶CD，有MN∶12=10∶20，解得MN=6.因而點(diǎn)M的坐標(biāo)是（12，6）.

點(diǎn)評 本題是一道雙動(dòng)點(diǎn)的兩條線段的最值問題，具有較大的難度.在解題過程中，學(xué)生要采用鏡像法畫出B點(diǎn)關(guān)于AC的對稱點(diǎn)，并使用勾股定理、三角函數(shù)、比例等方面的知識.

二、動(dòng)點(diǎn)問題教學(xué)建議

1.強(qiáng)化基礎(chǔ)教學(xué)

動(dòng)點(diǎn)問題是一類綜合性的問題，其涉及到初中數(shù)學(xué)中的幾何變換、函數(shù)、比例、等數(shù)學(xué)知識.因而學(xué)生深入理解數(shù)學(xué)基礎(chǔ)知識是解決動(dòng)點(diǎn)問題的基礎(chǔ).在教學(xué)中，教師講清楚數(shù)學(xué)知識的來龍去脈，并能夠理解這些概念和規(guī)律的內(nèi)涵和外延.在學(xué)生充分建構(gòu)起對基本概念和規(guī)律的理解后，教師還要引導(dǎo)學(xué)生解決一定量的問題，以保證學(xué)生遇到不同問題時(shí)能夠選擇對應(yīng)的解題方法.

2.開展針對訓(xùn)練

動(dòng)點(diǎn)問題類型較多，每一個(gè)類型有其獨(dú)特的解題方法.針對這個(gè)狀況，教師可以將初中數(shù)學(xué)中經(jīng)常出現(xiàn)的動(dòng)點(diǎn)問題進(jìn)行歸類，并開設(shè)習(xí)題課分類講解.教師在講解動(dòng)點(diǎn)問題時(shí)，可以讓學(xué)生發(fā)現(xiàn)新的解題方法，并將仔細(xì)體會(huì)這些解題方法.在課外，教師可以布置一定量的作業(yè)讓學(xué)生練習(xí)，以形成解題技巧的內(nèi)化.

參考文獻(xiàn)：

[1]王金鐸，宋炳忠.中考中的動(dòng)點(diǎn)問題[J].中學(xué)數(shù)學(xué)雜志，2003（6）：46-47.

[2]徐建兵.中考動(dòng)點(diǎn)問題的教學(xué)實(shí)例[J].試題與研究：教學(xué)論壇，2012（11）：47-48.

[3]施錦華.動(dòng)點(diǎn)問題教學(xué)之我見[J].中學(xué)教研（數(shù)學(xué)版），2010（6）：18-20.

[責(zé)任編輯：李 璟]

收稿日期：2020-01-15

作者簡介：張小娟（1980.10-） ，女，本科，中學(xué)一級教師，從事中學(xué)數(shù)學(xué)教學(xué)研究.