問題引領模型構建，面積轉化解法分析

卞明宇

[摘? 要] 函數背景中的面積最值問題是中考的經典問題. 各地中考試卷中出現了各式的面積問題，其問題特征和解法特點有一定的差異，所以開展面積最值問題探討對提升學生的解題能力有極大的幫助. 文章對2019年兩道中考函數面積最值問題開展思路突破，深入分析問題及解法，提出相應的教學建議，與讀者交流.

[關鍵詞] 二次函數;面積;對比;模型;分割法;轉化

二次函數中的三角形面積問題是近幾年中考的重要考查題型，其中涉及拋物線性質、三角形面積、最值分析等核心知識點. 對于不同的面積情形，所采用的面積模型構建、轉化方式也有較大的差異，下面對兩道二次函數背景下的三角形面積問題進行剖析.

兩道面積考題的思路突破

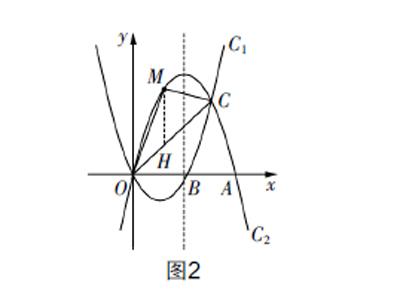
考題1? （2019年遵義中考數學第24題）如圖1，拋物線C1：y=x2-2x與拋物線C2：y=ax2+bx的開口大小相同、方向相反，它們相交于O，C兩點，且分別與x軸的正半軸交于點B和點A，OA=2OB.

（1）求拋物線C2的解析式.

（2）在拋物線C2的對稱軸上是否存在點P，使PA+PC的值最小？若存在，求出點P的坐標;若不存在，請說明理由.

（3）M是直線OC上方拋物線C2上的一個動點，連接MO，MC，點M運動到什么位置時，△MOC的面積最大？并求出最大面積.

思路分析? （1）拋物線C1和C2的開口大小相同、方向相反，則拋物線C2中的a=-1. 容易求得點B的坐標為（2，0），根據OA=2OB，可推導出點A的坐標為（4，0）. 將點A的坐標代入C2的解析式，即可求出b的值，從而確定C2的解析式.

（2）略.

（3）點M位于直線OC上方的拋物線C2上，求△MOC的最大面積時，可采用面積割補法，同時應充分利用點C和點O的坐標，故分割為兩個同底三角形時模型構建較為簡潔. 即，過點M作y軸的平行線，與直線OC交于點H，則S△MOC=S△MHO +S△MHC . 代入面積公式，即可得S△MOC= ·MH·（h1+h2）（h1和h2分別表示點O和點C到直線MH的距離），而h1+h2的大小可以表示為xC-xO . 設出點M的坐標，即可構建關于點M坐標參數的面積函數，利用函數性質即可確定△MOC面積的最大值. 需要注意的是，點M位于直線OC上方，故分析面積函數時需要考慮點M的橫坐標的取值.

過程突破? （1）分析可知a=-1，于是拋物線C2的解析式為y=-x2+bx. 容易求得點B的坐標為（2，0），又OA=2OB，所以點A的坐標為（4，0）. 將點A的坐標代入C2的解析式中，可求得b=4，所以拋物線C2的解析式為y=-x2+4x.

（2）略.

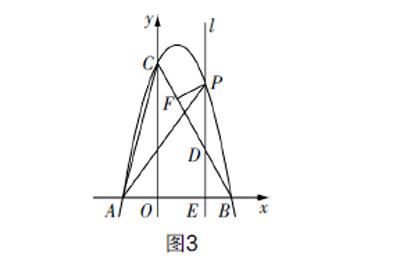
（3）可求得點C的坐標為（3，3）. 過點M作y軸的平行線，與直線OC交于點H，如圖2. 設點M的坐標為（x，-x2+4x），容易求得直線OC的解析式為y=x，所以點H的坐標為（x，x）. 所以MH=-x2+3x. △MOC的面積可以表示為S△MOC= ·MH·xC= ·（-x2 +3x） ·3=- x2+ x. 因為點M位于直線OC的上方，所以0

考題2? （2019年聊城中考數學第25題）如圖3，在平面直角坐標系中，拋物線y=ax2+bx+c與x軸交于點A（-2，0）和點B（4，0），與y軸交于點C（0，8），連接BC，又已知位于y軸右側且垂直于x軸的動直線l，沿x軸正方向從點O運動到點B（不含O點和B點），且分別交拋物線、線段BC以及x軸于P，D，E三點.

（1）求拋物線的表達式;

（2）連接AC，AP，當直線l運動時，求使得△PEA和△AOC相似的點P的坐標;

（3）過點P作PF⊥BC，垂足為F，當直線l運動時，求Rt△PFD面積的最大值.

思路分析? （1）由于點A和點B為拋物線與x軸的交點，故不需要構建復雜的三元一次方程組，可結合交點坐標將拋物線的表達式設為y=a（x+2）（x-4），然后將點C的坐標代入，即可確定a的值，從而完成拋物線表達式的求解.

（2）略.

（3）△PFD雖為直角三角形，但其頂點位置較為一般，無法直接利用條件來構建面積模型. 分析可知∠PDF=∠BDE=∠BCO，于是有△PFD∽△BOC. 利用相似三角形的面積關系可知，面積的比等于相似比的平方，因此可以通過分析△BCO的面積來確定Rt△PFD的面積. △BCO在坐標系中的位置較為特殊，有兩邊位于坐標軸上，可以較為簡捷地構建面積函數.

過程突破? （1）已知A（-2，0），B（4，0），所以可將拋物線的表達式設為y=a（x+2）（x-4）. 將點C（0，8）代入其中，可求得a=-1，化簡并整理后可得拋物線的解析式為y=-x2+2x+8.

（2）略.

（3）因為∠PDF=∠BDE=∠BCO，∠PFD=∠BOC=90°，所以△PFD∽△BOC. 所以 = 2. 所以S△PFD=S△BOC· 2，其中S△BOC= ·OB·OC=16，BC=4 . 可得S△PFD= PD2，即當PD取得最大值時，△PFD的面積取得最大值. 由點B和點C的坐標可求得直線BC的解析式為y=-2x+8，又點P位于拋物線上，所以可設點P的坐標為（x，-x2+2x+8），則點D的坐標為（x，-2x+8）. 可得PD=-（x-2）2+4. 分析可知當x=2時，PD取得最大值，且最大值為4，此時△PFD的面積也取得最大值，為 .

兩道面積考題的分析與思考

上述兩道考題的最后一問均求三角形面積的最大值，總體來看求解時均經歷了模型構建和最值分析兩個階段，考題圖像和解法均具有一定的特點，其轉化思路具有一定的借鑒價值，下面對其深入剖析.

1. 問題本質剖析

上述均為二次函數背景下的面積最值分析，結合拋物線的坐標特征，可知求解的實質就是將其轉化為關于點坐標的面積函數，屬于限定條件下的函數最值問題. 這是所有函數背景下面積問題的本質，因此求解過程離不開幾何模型構建和函數性質分析這兩步.

2. 問題圖像特征

問題的圖像特征直接決定了考題解法的選取. 考題1中所求最大面積的三角形雖為一般的三角形，但其中的兩個頂點的坐標（O和C）可求，因此可過動點M作分割線來構造圖形，合理利用頂點坐標來簡化函數模型. 考題2中所求最大面積的三角形雖為特殊的三角形，但無法直接構建動點P與點F之間的坐標關聯，這是不直接構建面積模型的原因，而與其相似的Rt△COB的位置特殊，且面積可求，因此可借此進行面積轉化.

3. 問題的解法特點

上述考題同為面積最值問題，其解法不同與問題圖像緊密相關. 其中考題1采用的是割補法，而考題2采用的是相似轉化法. 考題1中面積割補的關鍵是過動點作垂線來確定分割線，而利用交點的縱坐標是解法的根本;考題2中相似轉化的關鍵是確定相似三角形，而利用相似三角形面積比的性質是解法的根本. 但無論是面積割補法，還是相似轉化法，均是通過對特定問題圖像結構剖析而確定的最適解法，需充分把握解法的使用關鍵及本質內容.

考題探究的教學建議

1. 認真審題，把握問題圖像的結構特點

函數背景下的面積最值問題屬于中考典型的綜合性問題，理解題干條件，把握圖形特點是解題的關鍵，因此解題時需要認真審題，深入讀圖. 審題時，需要結合題干的文字信息來理解圖像特征，包括曲線與直線的位置關系、動點的移動軌跡、幾何圖形的頂點位置，以及區分圖像中已知與未知的條件. 例如上述考題2中的△OCB與目標三角形均為直角三角形，點B和點C的坐標已知，動點P在拋物線上運動，PD∥OC，點F的坐標未知等均是關鍵信息，也是后續確定相似轉化法的依據.

2. 合理選法，理解問題解法的本質

合理選定方法是破解面積最值問題的重要環節. 對于位置、頂點特殊的圖形，則可以采用直接構建的方式，而抽象且頂點一般的三角形則可以采用轉化法，常用的方法有面積割補法、相似轉化法、等積轉化法等，這些方法適用于不同的問題圖形. 學習時，需要深刻理解方法的本質，所用方法實則為等價轉化，其中滲透著模型思想和轉化思想，理解方法的思想內涵才能準確地選定方法、構建思路. 因此，教學中需要對面積問題的解法加以歸納，引導學生理解方法的內涵，掌握方法的使用技巧.

3. 重視思辨，提升學生解決問題的思維能力

提升學生的數學思維能力是考題教學的重點所在，尤其是歷年的中考壓軸題，具有極高的研究價值. 教學中，教師需要引導學生對考題進行整合，針對類型問題的解法進行辨析、探究，整體上把握問題的解析策略，如面積最值問題中需要關注問題的模型構建方法、最值分析方法. 同時，重視函數問題中的數形結合方法，合理利用數形結合分析策略來突破考題. 而在考題辨析過程中，則要多引導學生思考條件與問題之間的聯系，解題方法與問題特點之間的關聯，形成從問題特點入手，方法思想構思路的解題策略.