真實問題情境：連接現實世界與數學世界

摘要：真實問題情境是來自現實世界并蘊含著數學信息的綜合問題情境。真實問題情境的實踐模型包括潛入情境、超越情境、回歸情境。在教學中，要通過創設真實問題情境，引領兒童從現實世界走進數學世界，經歷數學知識的“再創造”，深化數學理解，積累數學化經驗，促進問題解決，進而用數學眼光觀察現實世界，用數學思維分析和解決現實世界中的問題。

關鍵詞：真實問題情境;現實世界;數學世界;小學數學教學

中圖分類號：G623.5 文獻標志碼：A 文章編號：1673-9094（2020）07B-0067-04

盡管數學哲學界關于數學對象問題爭論不休，但恩格斯所提出的“純數學的對象是研究現實世界的空間形式和數量關系，所以是非常現實的材料”仍然是經典見解。數學是反映現實世界的，然而數學必須完全舍棄現實世界的具體內容和質的特征，以純粹形態的量的關系和形式作為自己的對象，體現現實性與抽象性高度統一。兒童數學學習應經歷從具象到抽象、從經驗到理性的過程，實現現實性與抽象性的高度統一。真實問題情境是來自現實世界并蘊含著數學信息的綜合問題情境，它能夠引領兒童從現實世界走進數學世界，經歷數學知識的“再創造”，深化數學理解，積累數學化經驗，促進問題解決，進而用數學眼光觀察現實世界，用數學思維分析和解決現實世界中的問題。

一、真實問題情境的再理解

當前，我國的小學數學教學對情境的理解和實踐存在.定偏差：有的情境中不包含數學問題，只為引起學生注意而出現在導人部分;有的情境采用稚化教學，大量使用迎合兒童的熱門卡通形象，與現實世界毫無關聯;有的情境單純為了考查學生計算能力，出現了與實際情況嚴重不符的數據……這些情境的應用是低效的，甚至無效的，導致數學成績很好的學生也未必能解答簡單的現實問題。因此，我們應該對真實問題情境進行再理解。

1.以辯證視角看待情境的真實性

情境的真實性和熟悉度對學生開展數學研究有一定的幫助。真實問題情境會給學生帶來挑戰，就像他們在現實世界中遇到挑戰一樣。然而，這些情境不一定是真實的，也可能是根據教學需要而設定的。一般說來，數學教學中的真實問題情境具有以下特征：一是情境要有發生的可能性;二是提出的問題應該與校內外的情境相一致;三是解決方案的目的就像實際情境中一樣明確;四是應用的語言（如術語、句子結構等）要與實際情境相匹配。真實的問題情境中，問題的信息和數據應該是在實際情況中可能出現的，學生能夠使用在現實生活中可得到的方法解決問題，并以現實世界的標準來判斷解決方案的有效性，而執行任務的環境應該模仿真實情況[1]。

2.以問題引領增強情境的關聯性

美國數學家哈爾莫斯（P.R. Halmos）曾說過，“問題是數學的心臟”。在創設真實情境的數學教學中，問題是連接現實世界和數學世界的紐帶。真實問題情境信息豐富，有助于形成具有思維含量的真問題，有助于形成具有關聯性的問題鏈，也有助于學生獨立發現問題、提出問題。

數學問題來源于人類的生產生活實踐、自然科學研究和數學體系內部。針對教學任務，教師應綜合考慮生活現實和數學現實，選擇適宜的、包含數學問題的現實情境，除了學生個人情境、學校生活情境以外，也可以選用公共生活情境、職業情境、科學情境等，適當拓寬學生的學習半徑。這樣不僅能充分發揮情境對數學學習的支持作用，也能讓學生認識到數學學習可以為解決現實問題服務。好的數學問題能激發學生解決問題的積極性、主動性，一般包括以下特征：切中主題，清晰明確，難度適當，新穎獨特，啟發性強，促進數學知識的理解和掌握，等等。

二、真實問題情境的實踐模型

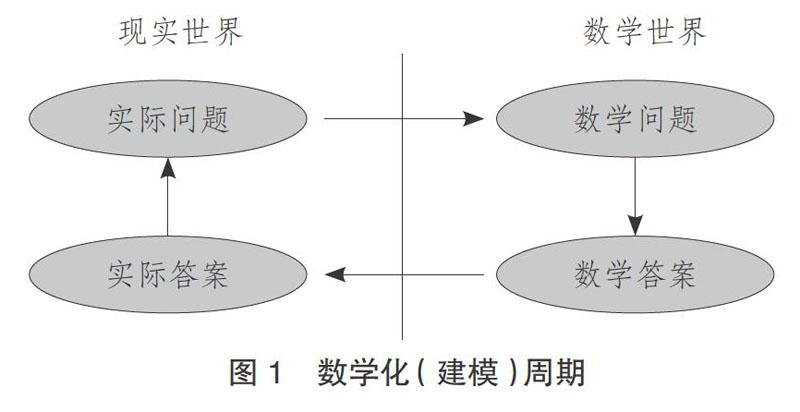
真實問題情境如何連接現實世界與數學世界？PISA測試框架中的數學化（建模）周期[2]（如圖1）形象地做出了說明。這一建模過程可簡略分為潛人情境、超越情境和回歸情境三個環節。

1.潛入情境

教師創設真實問題情境，學生通過文本或圖表的閱讀，提取與問題相關聯的數學信息，通過抽象、表征，逐步削減對現實的依賴，整合信息并用數學符號語言重新組織問題。通過這個環節，學生從現實世界“潛人”數學世界，將現實世界的話語轉換為數學世界的話語。

2.超越情境

情境中的問題已轉化為一個由抽象的數學對象組成的，能夠進行數學處理的問題。學生已完全超越現實情境而進入數學世界內部，可以利用已有的數學知識解決數學問題，或提出有意義的假設，嘗試運用創造性的方法解決數學問題。

3.回歸情境

將所得的數學答案放回現實情境之中，結合實際情況判斷答案是否符合實際或令人滿意，反思是否還存在其他可能。

這個建模周期描繪了一個利用數學解決現實世界問題的理想的、簡化的模型。在實際運用中，學生可能會在不同環節中來回移動，而不是按照建模周期單向發展。

三、真實問題情境的教學策略

情境的設置“對于引導學生開展數學探究起著思維定向、激發動機的作用”[3]。有關數學問題解決的研究發現，數學問題情境會影響學生的解題表現[4]。學生對可持續性問題或與生活有直接聯系的現實情境更感興趣，小數教育名家的經典課堂中有很多運用真實問題情境的精彩案例，通過他們的教學，我們能探尋出運用真實問題情境開展數學教學的基本策略。

1.經歷“再創造”過程，深化數學理解

弗賴登塔爾反復強調，傳統的數學教學傳授的是現成的數學，是反教學法的。學習數學的唯一正確的方法是實行“再創造”，也就是由學生本人把要學的東西發現或創造出來，教師的任務是引導和幫助學生去進行這種“再創造”的工作。真實問題情境能夠激活學生已有的知識，暴露學生真實的思維水平，為教師提供了解學生思維的機會，使教師能有針對性地開展教學。

徐斌老師在教學“平均數”時創設了“套圈游戲”的真實情境，讓所有學生當男女生比賽的“裁判”，課堂氣氛熱烈，學生沉浸其中。從第一輪男女生人數相等只需比較總數，到第二輪男女生人數不等不能輕易判斷……比賽進行到第四輪時學生產生了認知沖突——既不能比總成績也不能比最高分，此時學生感受到需要一個新的量來進行合理的比較。由于這個情境來源于現實世界，學生都有相同的比賽經驗，因而激活了他們“再創造”的靈感。這時有學生提出，要把兩隊成績平均一下，再比較平均數。徐老師立刻追問：平均數是一個什么數呢？學生各抒己見：差不多的一個數;在中間位置的數;比最多的要少一點，比最少的要多一點……學生用自己的語言表達出了平均數所具有的“集中趨勢”的深刻內涵。憑借真實問題情境，徐老師潤物無聲，教學無痕，“學生根據自己的經驗，用自己的思維方式，建構起自己的‘數學現實”[5]。

2.積累數學化經驗，促進問題解決

真實問題情境不僅能幫助學生深度建構數學知識，更能讓學生有機會親歷數學化過程，把現實世界中的問題轉換成能夠運用已有的數學概念與方法解決的數學內部的問題，然后通過求解數學問題來解決現實世界的問題。

張齊華老師在教學“舊小區里的電梯安裝”時引導學生提出了如何分攤電梯安裝費的問題，這是一個現實問題。通過討論，排除無關的陳述性信息，梳理出安裝費36萬元、共有7層14戶人家等有效的數學信息。此時，現實問題轉化為了“將36分為14個數的和”或“將18分為7個數的和”這樣的數學問題。學生通過小組討論，分別提出以等差數列的金額進行分攤和按比例進行分攤等方案。這些方案是學生根據數學思維、數學規則得出的，對于數學問題來說是正確的，但對于現實世界來說未必如此，還需考慮各種相關因素加以驗證并權衡[6]。數學教學的本質是問題解決，這一課例的研究過程與數學化建模相符。當學生面對現實世界時，必須能夠從實際問題情境中發現數學要素，通過文字、圖形與符號的相互轉換，進行數學建模和模型解釋，否則縱使學校數學學得再好，其數學能力也將無從展現。

3.嘗試多樣化情境，提升數學素養

數學學科核心素養是學生在數學學習時所應達成的綜合性能力，它具有綜合性、階段性和持久性的特征[7]。在數學教學中創設真實問題情境有利于發展學生的符號意識、模型思想與應用意識等核心素養[8]。在深入剖析內容本質和了解學生前概念的基礎上，如果能夠多樣化地選取不同的真實問題情境類型，能使學生的數學素養更為全面而豐厚。具體策略包括：（1）創設數學實驗的真實情境。例如，在教學“長方體和正方體的認識”時，為學生提供12根巧厘米、8根10厘米、4根8厘米的小棒，在真實的實驗情境中研究“能搭出幾種不同的長方體”這個問題。（2）創設數學史中的真實情境。例如，在教學“用字母表示數”時，引入畢達哥拉斯研究多邊形數的真實故事，通過點子圖認識平方數并進行拓展。（3）創設學校活動的真實情境。例如，在教學“復式統計表”時，以學校開展的垃圾分類綠色助學活動為背景，讓學生收集可回收物，經歷真實的統計活動。（4）鼓勵學生自己提出含有現實情境的數學問題。在這個過程中，一方面，問題提出者需要對問題進行數學意義的建構。另一方面，他們需要對實際情境有合理的考量：一個量發生了怎樣的變化？如何與其他的量發生數學意義上的相互關系？這種數學意義與實際情境的雙向建構，誰能說不是一種創造呢？[9]

4.開發拓展性課程，豐富數學活動

拓展性課程是以培育學生的主體意識、完善學生的認知結構、提高學生自我規劃和自主選擇能力為宗旨，著眼于培養、激發和發展學生的興趣愛好，開發學生的潛能，促進學生自主創新和研究實踐能力的開放性課程[10]。拓展性課程類型多樣、內容豐富，具有情境化、活動化、具身性、多元化等特征。

錢守旺老師在繪本《地球日，萬歲》的教學中，引導學生通過繪本閱讀掌握大數的讀寫方法和數位、計數單位等相關知識。通過對學生一周內喝飲料情況的調查統計，推算北京市小學生一年喝飲料的數量，幫助學生建立大數的數感，培養環保意識[11]。再如，不少學校開展了類似“游園課程”的數學拓展性活動課程，以現行數學教材“實境化”的整合和拓展為內容，以游園式體驗活動的方式，通過游戲化實施突出數學活動的真實性體驗，引導學生豐富和積累基本的活動經驗。如：“走迷宮”“跳跳棋”讓學生認識位置與方向，“踢球”“傳接球”讓學生理解基數與序數的意義，“報數排隊”“找朋友”讓學生認識10以內的數，等等[12]。

5.提供真實性問題，優化數學評價

史寧中教授指出：“數學教學的最終目標，是要讓學習者會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界。而數學的眼光就是抽象，數學的思維就是推理，數學的語言就是模型。”[13]純數學情境的問題和數學化的現實情境問題是無法較好地檢測學生數學素養水平的。在大力倡導核心素養的今天，學生數學知識的檢測、能力水平的測評和數學素養的評價應更多地選用真實問題情境，使學生獨立嘗試從實際背景中抽象出數學問題、構建數學模型尋求結果、解決問題的過程[14]。試以以下這道題目的解答為例：

2017年12月29日，汽油價格年內第十一次上調。北京市92號汽油價格調至6.84元/升，按一般家用汽車油箱50升容量估測，加滿一箱92號汽油比上調前多花約2.5元，則油價上調前為：

A.6.89元/升B.6.79元/升

C.7.34元/升D.6.34元/升

本題來源于生活實際，學生需要有一定的生活常識，比如“油價上調”“油箱容量”等，然后才能在數學閱讀的基礎上梳理出數學信息及其數量關系，再根據情境的實際意義建立求解模型。這與通常所見的模式化習題相比，具有更大的挑戰性，也更能測評學生是否真正掌握解決實際問題的能力。

數學知識來源于生活又超越生活，學生未來日常生活中遇到的數學問題，幾乎都是非常規的數學問題。在小學數學的教學中運用真實問題情境連接現實世界和數學世界，能有效激發學生的學習動機，使學生有機會經歷問題解決的全過程，提高問題解決能力，提升數學核心素養。

參考文獻：

[1][2]Kaye Stacey，Ross Turner.數學素養的測評：走進PISA測試[M].曹一鳴，等譯.北京：教育科學出版社，2017：78，62.

[3]呂傳漢，汪秉彝.論中小學“數學情境與提出問題”的數學學習[J].數學教育學報，2001（4）：10.

[4]Verschaffel L.Taking the modeling perspective seriously at theelementary school level：promises and pitfalls[R].Proceedings of the26th annual conference of the international group for the psychology ofmathematics education，Vol 1，U.K：Norwich，2002：67.

[5]徐利治，鄭毓信.現代教育工作者值得重視的幾個概念[J].數學通報，1995（9）：3.

[6]張齊華.“舊小區里的電梯安裝”教學實錄[J].小學教學（數學版），2019（6）：25-29.

[7]馬云鵬.關于數學核心素養的幾個問題[J].課程·教材·教法，2015（9）：38.

[8]金軒竹，馬云鵬.小學數學教學中真實情境的理解與設計策略[J].課程教學研究，2018（9）：71.

[9]于文華，蔡金法，劉美玲，等.美國小學數學教學中的問題提出及啟示——以West Park Place Elementary School為例[J].數學教育學報，2018（5）：64.

[10]劉延革，耿子文.基于核心素養培育下的拓展型課程概述[J].小學教學研究（教學版），2018（12）：55.

[11]錢守旺，李艷萍.通過繪本對接真實生活——《地球日，萬歲》繪本教學案例[J].小學教學（數學版），2019（7-8）：140-143.

[12]潘旭東，丁秀紅.小學低年級數學“游園課程”的開發與實踐[J].課程·教材·教法，2019（6）：100-106.

[13]史寧中.數學基本思想18講[M].北京：北京師范大學出版社，2016：前言2.

[14]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012：2.

責任編輯：楊孝如

本文系江蘇省教育科學“十三五”規劃重點自籌課題“基于發展關鍵能力的小學數學核心內容教學設計研究”（B-b/2018102/07）的研究成果。

收稿日期：2020-04-13

作者簡介：仲秋月，蘇州工業園區東延路實驗學校（江蘇蘇州，215123）科研處主任，教育碩士，蘇州市學科帶頭人，高級教師，蘇州市小學數學兼職教研員。