“直觀想象”核心素養的表現形式與培養途徑
朱鉉


摘 要:人們對“直觀想象”這一核心素養的含義理解不到位,存在片面或模糊.其實,直觀想象核心素養在中學數學中的主要表現形式為圖形直觀、空間想象和數形結合,應分別通過模型教學、找“高”訓練和數形結合來培養學生的直觀想象核心素養.
關鍵詞:直觀想象;數形結合;模型教學;核心素養
中學數學的六大核心素養:數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析,其實并不是什么新的東西,人們對數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析這五大素養都能正確地理解它的含義,唯獨對“直觀想象”這一核心素養的含義理解不到位.實際上,《普通高中數學課程標準(2017年版)》給出了直觀想象的明確定義:直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化,利用空間形式特別是圖形,理解和解決數學問題的素養.其主要包括:借助空間形式認識事物的位置關系、形態變化與運動規律;利用圖形描述、分析數學問題;建立形與數的聯系,構建數學問題的直觀模型,探索解決問題的思路[1].因而直觀想象核心素養在中學數學中的主要表現形式為圖形直觀、空間想象和數形結合,那么我們應當如何培養學生的直觀想象能力呢?
一、利用平面幾何中的“基本模型”培養學生的幾何直觀
平面幾何是立體幾何和解析幾何的基礎,在平面幾何的學習過程中,學生的識圖和作圖能力得到了培養,而對圖形的辨別、拆分與重組能力就是“直觀想象”核心素養的表現形式之一.在平面幾何的學習中,有許多基本圖形以及它們所得到的結論我們稱之為“基本模型”,許多看似復雜的圖形實際上都由這些基本模型組合而成的,記憶和熟練掌握這些基本模型,并能從復雜圖形中辨認它屬于哪一類基本模型,或是由哪些基本模型復合而成,這就是直觀想象的核心素養水平達成的表現.
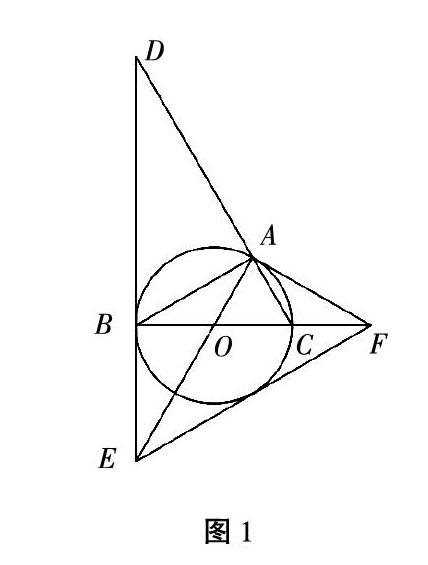
例1 如圖1,⊙O是ΔABC的外接圓,BC是⊙O的直徑,∠ABC=30°,過點B作⊙O的切線BD,與CA的延長線交于點D,與半徑OA的延長線交于點E,過點A作⊙O的切線AF,與直線BC的延長線交于點F.
(1)求證:△ACF∽△DAE;
(2)若S△AOC=,求DE的長;
(3)連接EF,求證:EF是⊙O的切線.
這里著重說明圖形的辨別與拆分,所以略去解答過程.本題的圖形看似復雜,實際上它是由以下四個基本模型復合而成的:圖2的弦切角模型,圖3的等腰梯形模型,圖4的直角三角形模型以及最常見的等腰三角形模型.這幾個基本模型是平時學習和練習過程中常見的,學生對它們可得出什么結論非常了解,只要將復雜圖形中的基本模型辨別出來并進行拆分,學生就不難找到解題的思路和方法.而對復雜圖形的辨別和拆分能力就是“直觀想象”核心素養的一種表現,日常教學過程中引導學生注重基本模型的研究,吃透基本模型,然后強化對復雜圖形的辨別和拆分能力的訓練,不僅能提高學生的解題能力,還能提升學生“直觀想象”的核心素養.
基本模型既包括定義、定理的代表圖形,又包括在生活中、練習中經常遇到的圖形,還包括由實際問題抽象出來的數學問題.在教學過程中,教師應善于引導學生整理歸納出基本類型和方法,并把類型、方法和范例合為一體形成“基本模型”來記憶和積累.當遇到一個幾何問題時,我們能辨認和拆分它們并以此為索引,在記憶貯存中提取出相應的方法來加以解決,這是培養學生“直觀想象”核心素養的一種方法.
二、利用找“高”訓練培養學生的空間想象
在立體幾何中,“高”常扮演“關鍵先生”,從簡單的三視圖到復雜的求二面角的平面角,都能見到“高”的身影,然而,我們的“關鍵先生”往往不容易找到,因此在立體幾何教學中,培養學生找“高”能力是培養學生空間想象的重要途徑,而空間想象是“直觀想象”的另一種表現,培養學生的空間想象能力就是培養學生“直觀想象”的核心素養.
例2 某四棱錐的三視圖如圖5所示,試畫出些四棱錐的直觀圖.若三視圖如圖6所示呢?
設計意圖:給出實物畫三視圖,給出三視圖畫直觀圖是培養學生空間想象非常有效的途徑,學生在不斷地構建的過程中,空間想象能力逐步培養和增強,而給出三視圖畫直觀圖的關鍵是找到幾何體的“高”所在的位置.本例通過改變側視圖和俯視圖的形狀達到訓練學生找”高”能力的目的(作畫略).
例3 在四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD為矩形,AP=AB=■BC,Q為BC的中點,求二面角A-PD-Q的余弦值.
本例是求二面角的常見例題,但在教授本例時,我們不應滿足于用空間向量來求二面角,而應引導學生在這一基礎上,探索采用邏輯法(演繹法)來求二面角,從而使學生的空間想象和邏輯推理能力都得到培養.
采用邏輯法(演繹法)來求二面角的關鍵是要找到一個平面到另一個平面的垂線,也就是“高”.要想找到這一條“高”我們就要找到面面垂直,利用面面垂直的性質定理來找“高”,面面垂直的性質定理告訴我們,在一個平面內作交線的垂線,必與另一個平面垂直.所以我們只要找到面面垂直,再在一個平面內向另一個平面作交線的垂線即可,通過這種訓練,學生逐步構建起線線關系、線面關系和面面關系,并逐漸明晰它們之間的關系,從而構建起自己的空間體系,符合了構建主義的學習和教育觀.
三、注重數形結合思想的滲透,培養學生的核心素養
《普通高中數學課程標準(2017年版)》指出:利用圖形描述、分析數學問題;建立形與數的聯系,構建數學問題的直觀模型,探索解決問題的思路.腦科學告訴我們,人類處理圖形的能力先于且強于文字能力,所以說數形結合思想是人類將復雜、抽象問題簡單化的一種重要思想.實際上,數形結合的思想貫穿于整個中學數學,從初一的數軸到高中的函數,從初中的解方程應用題到高中的解析幾何等,數形結合的身影無處不在.
雖然大家都知道數形結合思想的重要性,但很多教師在教學過程中仍然熱衷于無圖推理,美其名曰培養學生的邏輯推理能力,殊不知數學有六大核心素養,邏輯推理只是其中的1/6,我們應當大力推行數形結合,提出“不作圖就不做數學題”的口號.比如說,在解一元二次不等式ax2+bx+c>0(a≠0)的教學中,當Δ>0時,學生在解出一元二次方程ax2+bx+c=0(a≠0)的兩根后不會得出不等式的解集,這時教會并要求學生一定要畫圖,利用數形結合思想來解一元二次不等式,不僅能使學生理解解不等式的原理,還能減少學生的錯誤.同時,當Δ=0或Δ<0時,不等式ax2+bx+c>0(a≠0)的解集如何取得,是學生的學習難點,利用數形結合思想能輕松突破這一難點.
四、結語
數學家笛卡爾早就說過:“沒有圖形就沒有思考”.美國數學家斯蒂恩斯也說:“如果一個特定的問題可以轉化為一個圖像,那么就整體地把握了問題,并且能創造性地思索問題的解法”.通過圖形,人們能夠更直觀地理解事物的本質,這就是人們常說的“用圖形說話”.所以培養學生的直觀想象核心素養就是要讓學生學會用圖形思考,用圖形說話,能從圖形中洞察解決問題的線索.我們在教學中應當關注培養學生的圖形直觀、空間想象和數形結合,并堅定不移地貫徹在整個中學數學教學過程中.
編輯 李建軍

