“游戲化教學”讓數學課堂效率更高
程偉

【教學內容】
蘇教版《數學》五年級(下冊)第85-87頁。
【教材分析】
本節課是在學生學習了幾種平面幾何圖形之后進行教學的,學生對平面圖形中的點、線、面以及軸對稱圖形等基本概念已經有了初步的認識。在此基礎上,教師從日常生活中的實物及圖形引出網的概念。對于“網”的認識,讓學生認識曲線圖形,為學生進一步學習網的周長和面積計算作鋪墊,也為學生將來學習立體圖形的有關知識打下堅實的基礎。
【教學目標】
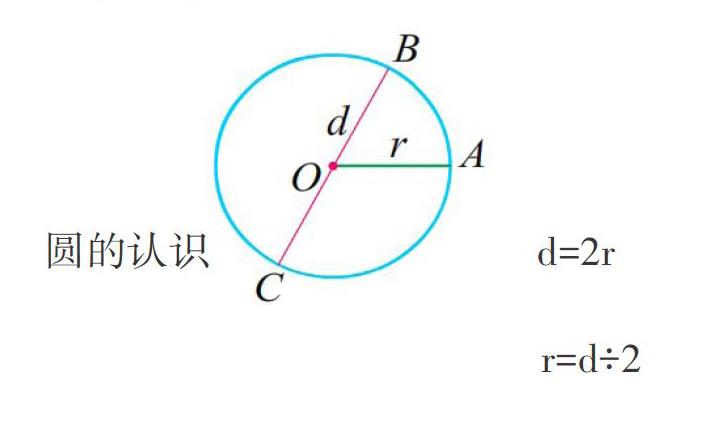
1.認識圓,知道網各部分的名稱;掌握網的特征,理解直徑和半徑之間的關系。
2.學會用網規畫規定大小的網。
3.通過直接觀察和動手操作,在充分感知的基礎上理解網的概念,了解網的特征,在活動中培養觀察能力、空間想象能力以及抽象概括能力,并能運用所學的數學知識解決生活中的實際問題。
【教學重難點】
1.認識網各部分名稱及其特征,了解半徑與直徑的關系,初步學會用網規畫圓。
2.用圓的知識來解釋和解決生活中的實際問題。
【教學過程】
一、游戲引入,激發興趣
師:同學們喜歡玩游戲嗎?今天孫悟空和豬八戒也在玩游戲,我們一起去看看吧。
課件演示:孫悟空和豬八戒在玩捉迷藏的游戲,悟空藏了起來,悟空藏在距離八戒5米遠的地方,你能幫助八戒找到悟空嗎?用一個點代替八戒,用5厘米代替5米,在圖上畫出悟空在哪里。
生動手操作,教師巡視,并提問:除了你表示的那個點,還有其他的可能嗎?
師:剛才我看到許多同學找到了這個點,你同意嗎?我還看到有些同學畫了這些點,對嗎?還有其他的可能嗎?
課件演示:點越來越密,最后形成了一個圓。
師:悟空在哪里?對,就在這個圓上。
師:今天,我們就一起學習有關“圓”的知識。
師板書:圓的認識。
(設計意圖:通過學生感興趣的捉迷藏游戲引出本節課的內容,提升學生的學習興趣。同時,學生在游戲的過程中初步感知網的幾何定義:平面上定點的距離等于定長的所有點組成的圖形叫做網。)
二、聯系實際,整體感知
1.尋找生活中的圓。
師:其實在生活中我們經常見到圓,同學們能說一說在生活中見到的圓形物體嗎?
生舉例說出生活中見到的圓。
2.利用身邊的物體初次畫圓。
師:剛才同學們舉例說出了生活中常見的圓形物體,那么你能用這些圓形物體畫一個圓嗎?注意在畫的過程中比較畫圓和畫其他平面圖形的不同之處。
生操作并思考。
(設計意圖:讓學生利用身邊的物體畫網,在畫的過程中體會網和其他平面圖形的區別。生活化的教學方式能引起學生的興趣,學生也更容易理解所學知識。)
3.交流、討論圓和多邊形的關系。
師生交流并總結圓和其他多邊形的聯系和區別:圓和其他多邊形都是平面圖形,但是其他多邊形都是由線段圍成的,而圓是由曲線圍成的。
師:難怪古希臘的一位數學家曾說,在一切平面圖形中圓形是最美的。
4.用圓規畫圓。
師:古人說過“不以規矩,不能成方圓”。你知道這里的“規”指的是什么嗎?其實就是圓規,圓規是專門用來畫圓的工具。老師看同學們都有了這個工具,那么你們能試著用圓規這個工具畫一個圓嗎?
生動手操作,嘗試用圓規畫圓。
師:同學們畫的圓漂亮嗎?
教師展示學生作品并提問:為什么我們用專門畫圓的工具畫圓,卻畫得不漂亮呢?問題出在哪里?
生交流討論并找出原因:畫圓的時候圓規移動了,圓規兩腳間的距離發生了變化。
師:工欲善其事,必先利其器,所以讓我們重新來認識畫圓的工具——圓規。
師介紹圓規。
師:現在你能用圓規畫一個漂亮的圓嗎?再畫一次試試。
生動手操作,教師展示學生作品。
師:這一次大家畫的圓都很漂亮,其實想要畫一個圓并不難,只要能按要求正確操作,同時多練習就可以了。那么,現在請大家對比一下你畫的圓和同桌畫的圓一樣大嗎?同樣是圓,為什么有的大有的小呢?
生討論得出結論:因為圓規兩腳間的距離不同。
師:如果圓規兩腳間的距離是一個確定的數值,是不是畫出的圓就一樣大呢?把圓規兩腳間的距離定為3厘米再次畫出圓,畫好之后和同桌對比看看你們畫的圓是否一樣大。
(設計意圖:直接讓學生利用網規畫圓,因為大多數學生在準備網規的時候就已經能白己畫圓了。在畫的過程中發現問題并由學生討論解決,教師只要適時引導學生總結畫圓時需要注意什么,再交流怎樣畫指定大小的圓。)
5.動手折疊圓形紙片并學習圓的各部分名稱。
師:請同學們拿出圓形紙片,對折打開,換一個方向再對折打開,多折疊幾次,你發現了什么?把你的發現和同桌交流。
生操作并交流發現:所有的折痕相交于一點.每條折痕都一樣長,而且交點把折痕分成了相等的兩部分。
師:同學們認為這個交點和我們剛才用圓規畫圓的哪一點一樣呢?
生:圓規針腳固定的那一點。
師:請同學們自學書中的知識。通過自學你知道了哪些關于圓的知識?
生交流圓心、半徑、直徑并能通過練習準確掌握半徑和直徑的概念。在自己畫的圓上畫出圓心、半徑和直徑,同時用字母表示。
(設計意圖:在教師的指導下,學生動手操作,閱讀書中相關文字材料,主動獲取知識,這樣就深刻理解了網心、半徑、直徑等概念。)
三、探討交流,加強認識
1.在活動中探究圓的特征。
師:剛才我們折疊圓形紙片的時候,折痕就是圓的直徑,折痕相交的點就是圓心,圓心把直徑分成相等的兩部分,每部分都是圓的半徑。同學們,同一個圓內能畫出多少條半徑?它們的長度都相等嗎?
生操作,討論得出結論:圓有無數條半徑,而且長度都相等。
師:那么同一個圓內能畫出多少條直徑呢?它們的長度又怎樣?請同學們再次折一折手中的圓形紙片并互相交流想法。
生通過實際操作得出結論:同一個圓內有無數條直徑并且長度都相等。
師:在同一個圓里有無數條半徑和直徑,而且它們都相等。
小結:圓,一中同長也。
師:那在同一個圓內半徑和直徑又有什么關系?
生:在同一個圓內直徑是半徑的2倍,半徑是直徑的一半。
師:通過對折疊圓形紙片你還發現了什么?
生探討交流得出結論:圓是軸對稱圖形,有無數條對稱軸。
(設計意圖:讓學生白己通過觀察、操作、比較、總結,最后感知網的特征,通過“折一折”“面一畫”“量一量”,讓學生探究網的特征,這樣的道程讓學生品嘗到了成功的喜悅。讓學生在做中學,在學中做,培養了學生動手實踐的能力,激發了學生探索知識的興趣。)2.在練習中鞏固圓的知識。用我們剛才的知識解決問題,請填寫下表:
(設計意圖:學以致用,通過練習加深學生對直徑和半徑之間關系的理解。)
3.在游戲中提升對圓的認識
師:(課件出示捉迷藏的游戲)還記得悟空可能藏在哪里嗎?誰能用今天學習的知識將圓描述出來。
生:悟空藏在以八戒為圓心半徑為5米的圓上。
師:一定是這樣嗎?悟空會不會藏在距離八戒5米的地底下呢?還有可能藏在哪里呢?
學生交流得出:悟空藏在以八戒為球心半徑為5米的球上。
師生交流:圓和球體都是“一中同長”,圓是平面圖形,球是立體圖形。
(設計意圖:通過游戲讓學生突破原有的認識,網和球都是“一中同長”,增長了學生的知識,同時和課的開始相照應。)
四、小結
本節課你學到了哪些知識?你能用這些知識解決哪些問題?
五、作業
完成課后“練一練”。
板書設計:(作者單位:江蘇省盱眙縣桂五鎮中心小學)

