注重首因效應，構建數學模型

陳旭芳

摘要：目前初中數學課堂教學中新知識的引入多以講概念、定理為主，教師教得枯燥，學生聽得乏味，這種現象導致不少學生對學習數學缺乏興趣，甚至產生厭倦心理。本文通過“巧用情境、善用分析、妙用猜想、活用分類”的方式方法，在第一時間誘發學生學習數學的欲望，注重首因效應，構建數學模型，既而產生持久的學習數學的動力，培養數學核心素養。

關鍵詞：首因效應；數學模型；情境創設；核心素養

中圖分類號：G633.6文獻標識碼：A文章編號：1992-7711（2020）03-0122

當人們參加面試，或開始著手一份新的工作，或進入一個新的環境，或會見一位重要的人物時……人們總是竭盡全力，給他人留下一個良好的第一印象。這一現象反映了人們的一種普遍的認識，即第一印象是極為重要的。這種認識在心理學上稱為首因效應。

首因效應是對人或對事物的第一眼觀，是腦海中定格下來的第一印象，往后對這件事或人的好壞、或長或短的認知極大一部分取決于第一印象。為何現在的學生談及數學學習時往往會覺得困難重重，甚至有些學生談其色變，對數學學習有著強烈的抵觸情緒？學生的種種表現與首因效應有不可分割的關系。其本質原因——數學作為基礎學科其內容較為抽象，一些知識的學習與理解需要“悟性”，對學生的理解能力與思維能力有著極大的挑戰。尤其是由小學到初中的過渡，從知識內容到學習方法都會讓部分學生感到困惑，這種“急在心里的”的狀況值得我們教師去思考其因，探究其法，從而幫助學生改變現狀。筆者在教學過程中進行了以下四個方面的嘗試，把抽象的數學概念一般化、具體化，順其自然地構建數學模型，學生的核心素養便在潛移默化中形成。

一、巧用情境，激發首因效應——構建“符號”模型

蘇霍姆林斯基曾說：“不管什么類型的老師如果想要得到學生們的認可，那就必須在自己的課堂上激發學生們的學習興趣，讓自己的課程充滿魅力，來吸引學生的目光。”筆者通常會著手這兩方面：一是找到切入點，通過使用多媒體來輔助教學；二是了解學生的興趣點，在教學時多準備一些學生感興趣的事物，盡量讓更多的學生參與課堂。

案例1在進行浙教版七年級上冊《4.1用字母表示數》教學時，筆者創設如下情境引領學生學習新知。

兒歌動畫——數青娃（多媒體課件展示，如圖）

1. 1只青蛙，1張嘴，2只眼睛，4條腿，

1聲撲通跳下水；

2. 2只青蛙，2張嘴，4只眼睛，8條腿，

2聲撲通跳下水；

3. 3只青蛙，3張嘴，6只眼睛，12條腿，3聲撲通跳下水。

建構“符號”模型：借助多媒體展示的情景動畫，一只只青蛙隨著歌聲依次入水。學生齊唱，n只青蛙，n張嘴，2n只眼睛，4n條腿，n聲撲通跳下水……學生經歷了一個以實際情景為先驅，化抽象為具體的過程，能更好地體會數學，理解數學符號。

說明：以一首兒歌貼切而自然地引入，使學生體會到現實生活的規律性及用字母表示這一規律的可行性和必要性，進而使學生在輕松活潑的氣氛中感受著用字母表示數。學生在課堂上享受到了學習的樂趣，在實現寓教于樂的同時培養他們學習數學的興趣。

二、善用分析，達成首因效應——構建“方程”模型

陶行知先生曾提出生活即教育的教育主張。因此，筆者時常將貼近生活的素材融入到課堂中，以輔助教學的開展。

案例2在進行浙教版七年級下冊《2.1二元一次方程組》教學時，筆者抓住今年是建國70周年這一靈魂事件，吸引學生眼球，建構“方程”模型，對課堂教學做如下設計。

課前觀看我國建國70周年的閱兵式片段，拋出問題，學校組織各班少年警校的同學參加校國慶晚會，要求男生戴藍色警帽，女生戴紅色警帽。每位男生看到藍色與紅色的警帽一樣多，而每位女生看到藍色的警帽比紅色的多1倍，你知道該班參加國慶晚會的男生與女生各有多少人嗎？

研究分析：男生看警帽時，看到的藍色警帽應是男生人數-1頂；

女生看警帽時，看到的紅色警帽應是女生人數-1頂。

構建“方程”模型：假設男生有x人，女生有y人，男生看到的男生和女生的警帽數目的一樣多的，轉化為女生和男生的關系為：男生人數-1=女生人數，寫成方程為：x-1=y.女生看到的是男生的警帽=2×女生的警帽，把他轉化成男生和女生的關系為：男生人數=2（女生人數-1），寫成方程為x=2（y-1）。把所列方程聯立成方程組，在觀察分析的過程中學會尋找已知量與未知量，找準等量關系，建立方程或方程組。

說明：在此過程中，讓學生通過自己的觀察、探索、嘗試、比較等活動去發現一些數學規律，體會轉化的思想與方程的思想在應用題中的應用。同時讓學生體會從實際問題情境中抽象出二元一次方程組的過程，從而培養學生分析問題、解決問題的能力，以及運用數學知識解決實際問題的能力。

三、妙用猜想，增強首因效應——構建“函數”模型

在教學中我們要善于利用“首因效應”，它在本質上是一種優先效應，當不同的信息結合在一起的時候，人們總是更加重視第一時間出現的信息。因此，在平時的授課過程中，要切實把握好“首因效應”，以取得更好的教學效果。

說明：銳角三角函數是聯系三角形邊角之間關系的橋梁，然而銳角三角函數的概念比較抽象，較難理解，呈現學生熟悉登山情景，從已有經驗出發，探究其中的數量關系，銳角三角函數概念的形成便是水到渠成的事。由于這是九下第一章的起始課，情景呈現，拋出問題，既提高了學生學習的積極性，又消除了學生學習銳角三角函數的畏難情緒。此模型建立在學生原有認知的基礎上，由特殊到一般的實驗方法探索銳角與幾類線段比之間對應關系，從而概括出銳角三角函數的概念。

四、活用分類，促成首因效應——構建“圖形”模型

數學教學應遵循辯證唯物主義認識論的基本觀點，從直觀到抽象、從感性到理性，通過操作、畫圖等途徑，理清圖形間的微妙關系。

案例4在進行浙教版九年級下冊《2.1直線與圓的位置關系（1）》教學時，為了增強學生的空間想象能力和邏輯推理能力，筆者是這樣開展的：

請學生仔細觀察一輪紅日從海平面升起的整個運動過程，并截取有代表性的三幅圖片，把它們抽象成幾何圖形，得出直線與圓有三種位置關系。從直線與圓的公共點的個數來判斷，從圓心到直線的距離d與半徑r的數量大小關系來判斷。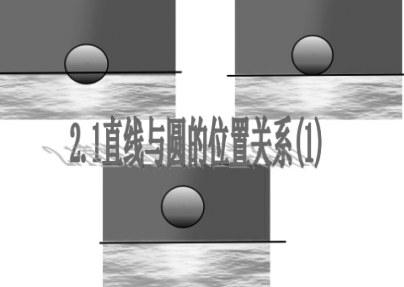

建構“圖形”模型：當直線與圓有兩個公共點時，叫做直線與圓相交；當直線與圓有唯一個公共點時，叫做直線與圓相切，這個公共點叫切點；當直線與圓沒有公共點時，叫做直線與圓相離。

說明：動態過程的呈現，一方面能讓學生迅速從看似簡單的現象中發現規律，進而培養學生發現問題、探索問題的能力；另一方面有利于學生把實際問題抽象成數學模型，并運用分類的方法從直線與圓公共點的個數，給出三種位置關系的概念，學生很容易接受。此次建構“圖形”模型，首先印入眼簾的是這三幅圖中太陽與海平線的位置特點，對接下來學生形成這三種位置關系的概念產生了積極影響，學生對三種位置關系的區分也有了更好的識記。這時，再讓學生探究直線與圓位置關系相應的數量關系時，運用類比遷移、大膽猜想、實驗驗證的方法去發現直線與圓的位置關系可通過半徑與圓心到直線的距離的數量關系來判斷是顯而易見的事。

初中生的年齡特征決定了他們對事物好惡的片面性、隨意性及遷移性。他們的認識水平及邏輯思維還不夠成熟，辯證思維還剛開始形成，他們往往只憑某一點的好壞，憑直覺下判斷、做推理、得出結論。當他們的第一印象比較好時，就會把這種“好感”遷移到他們所學的學科上。當學生期待某一章節的第一節課時，當學生聆聽教師每節課的第一句話時，他們一般都抱著急于見一見“廬山真面目”的心理，期待著能夠得到心理上的滿足，渴望得到成功的樂趣。因此，我們對這些首因效應不能掉以輕心，要精心設計，要給學生創造良好的首因效應的氛圍，為今后的數學教學開個好頭，打好基礎。

參考文獻：

[1]劉國清.初中數學教學中應注重“首因效應”[N].貴州民族報，2014-07-07（C02）.

[2]張富儉.淺談“首因效應”在數學教學中的應用[J].數學學習與研究（教研版），2009（9）：62.

（作者單位：浙江省紹興市元培中學312000）