過程經(jīng)歷：探索從“合情”走向“合理”

丁洪

[摘 要]探索一般經(jīng)歷“合情”和“演繹”兩個推理階段。以“有趣的乘法計算”的教學為例，以形式概括為主的過程浸潤合情推理，通過例子多類型、比較多角度和聯(lián)系多層次，自主建構(gòu)規(guī)律的外在形式;以實質(zhì)把握點睛的過程浸潤演繹推理，通過表征梯度化、反思體系化和遷移立體化，刻畫規(guī)律的內(nèi)在道理。“合情”和“演繹”兩者相輔相成和辯證統(tǒng)一，共同服務(wù)學生的素養(yǎng)培養(yǎng)和未來發(fā)展。

[關(guān)鍵詞]過程經(jīng)歷;計算教學;探索規(guī)律

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）11-0004-03

計算教學需要緊扣兩大任務(wù)，即“算法掌握”和“算理把握”。其中，算法指向運算的操作程序，主要解決“可以怎樣算”的問題，這個過程注重計算順序的有效識記和遷移運用，主要培養(yǎng)學生的運算能力，“熟能生巧”是其理念支撐;算理聚焦運算的數(shù)學道理，主要解決“為什么可以這樣算”的問題，這個過程注重計算規(guī)則的透視解構(gòu)和合理重構(gòu)，主要培養(yǎng)學生的推理能力，“熟能生智”是其教學訴求。顯然，計算教學需要引導學生既經(jīng)歷由表及里的深度學習過程，也經(jīng)歷由內(nèi)而外的生長拓展過程。

“有趣的乘法計算”是蘇教版教材三年級下冊“探索規(guī)律”的專題活動，它的知識基礎(chǔ)是兩位數(shù)乘兩位數(shù)，屬于計算教學的范疇。從探索規(guī)律的角度看，教學的流程一般是固化的，分為“識別計算對象”“發(fā)現(xiàn)計算規(guī)律”“表達計算規(guī)律”“驗證計算規(guī)律”四個環(huán)節(jié)，它們環(huán)環(huán)相扣、封閉自洽和自成一體;從計算教學的角度看，一般注重觀察、比較、歸納和驗證，往往缺失算理的融入、思維的卷入和情感的投入，看似“有趣”，畢竟“不實”。那么，怎樣做才能讓探索過程不再流于形式？怎樣做才能讓探索活動保質(zhì)增效？怎樣做才能讓學生的探索能力得到可持續(xù)發(fā)展？顯然，要處理好這些問題，必須緊扣算法和算理，厘清探索的形式與實質(zhì)，并做好形式向?qū)嵸|(zhì)的必要跨越，實現(xiàn)兩者從“湯水分離”走向融合共生。

一、形式概括為主，經(jīng)歷合情推理

形式概括一般遵循“所見”即“所得”的原則，這種推理過程以觀察為起點，以聯(lián)系為紐帶，以典型案例的分析和對比為重點，然后在變化中確定不變的因素，并將不變的內(nèi)容用簡潔的語言記錄下來。簡而言之，眼見為實，規(guī)律再現(xiàn)，合乎情理。但是，這種推理的結(jié)果未必為真，只是一種或然的結(jié)論而已。

1.例子多類型

好的例子有利于分門別類地探索問題，有助于知識的邏輯建構(gòu)和思維的有序生長。從教的層面看，適合探索的例子要有代表性和典型性，要能反映研究內(nèi)容的不同層次。比如，在“兩位數(shù)乘11”的板塊中，教材先后出現(xiàn)兩組探索對象，分別是24×11、53×11、62×11和23×11、64×11、59×11。在這6道算式中，前4道為同一類，屬于“兩頭一拉，中間相加”的類型;后2道略有變化，除了滿足基本類型的要求外，還增加了“滿十進一”的特殊情況。其實，這兩組例子并沒有列舉出“兩位數(shù)乘11”的所有情況，如果學生學有余力，教師還可以順勢給出形如“95×11”的例子，引導學生體驗“連續(xù)進位”的復雜情況。在“同頭尾合十”的板塊中，“同頭”所在的十位上，數(shù)字1～9都出現(xiàn)了，“尾補”所在的個位上，數(shù)字組合1和9、2和8、3和7、4和6、5和5也都出現(xiàn)了。從學的層面看，學生舉例驗證的時候，也需要考慮所選例子的適切性和覆蓋面。顯然，無論是舉例教學，還是舉例驗證，這項技能都不是與生俱來的，需要不斷修煉、調(diào)整和磨合，直至學會全面考慮問題。

2.比較多角度

相對于“善于舉例”而言，“善于比較”更能體現(xiàn)數(shù)學學習的本質(zhì)。對于小學生而言，比較一般是在教師的指導下完成的，并且指向思維的不斷優(yōu)化。一方面，比較發(fā)生在思維的橫向擴展中，如“兩位數(shù)乘11”的學習，先從不進位的情況開始探索，通過反復觀察和比較異同，發(fā)現(xiàn)不同豎式中存在相同的對應(yīng)關(guān)系，即積的個位上的數(shù)等于“兩位數(shù)”個位上的數(shù)，積的百位上的數(shù)等于“兩位數(shù)”十位上的數(shù)，積的十位上的數(shù)恰好等于“兩位數(shù)”個位和十位上的數(shù)字和，形象概括成“兩頭一拉，中間相加”。不過，規(guī)律在“64×11、59×11”這樣的算式中并不起作用，思維沖突引發(fā)繼續(xù)對比的需求，對比后發(fā)現(xiàn)“兩位數(shù)”十位上與個位上的和發(fā)生了變化：原來小于10，現(xiàn)在等于或者大于10，根據(jù)“十進制”的計數(shù)規(guī)則，“滿十就要進一”。顯然，有梯度的橫向擴展，更有助于思維的有序遞進。另一方面，比較發(fā)生在思維的縱向發(fā)展中，如“同頭尾合十”的學習，一是看著比，比出“兩個乘數(shù)十位上的數(shù)相同”“兩個乘數(shù)個位上的數(shù)相加都等于10”;二是算著比，比出“積的末兩位等于兩個乘數(shù)個位上的數(shù)相乘”;三是聯(lián)著比，在運用探索規(guī)律直接寫出得數(shù)的情況下，比出“形如（a-1）（a+1）與a×a的乘法算式結(jié)果相差1”。顯然，有深度的縱向發(fā)展，更有助于思維的螺旋上升。

3.聯(lián)系多層次

多層次的聯(lián)系有助于數(shù)學知識的系統(tǒng)化、結(jié)構(gòu)化和模型化，使探索活動服務(wù)于學生思維。首先，聯(lián)系程序性知識進行計算，“有趣的乘法計算”源自“兩位數(shù)乘兩位數(shù)”，因此“兩位數(shù)乘兩位數(shù)”的計算過程是否合理，計算結(jié)果是否正確，是探索這類計算現(xiàn)象的前提，具有“一票否決”的地位;其次，聯(lián)系概念性知識進行猜想，通過“一個兩位數(shù)與11相乘的得數(shù)有什么共同特點？先用豎式計算，再分別把積的每一位上的數(shù)和原來的兩位數(shù)比較。”“積的末兩位是怎樣算出來的？末兩位前面的數(shù)呢？”等的追問，激發(fā)學生調(diào)用“數(shù)的組成”“表內(nèi)乘法”“簡單加減”等先擁概念進行一系列的猜想，有效避免了表達時“言之無物”;最后，聯(lián)系價值性知識進行反思，學生體會到“可以通過仔細觀察和比較發(fā)現(xiàn)規(guī)律”的探索艱辛，也體驗到“發(fā)現(xiàn)規(guī)律后，要通過計算進行驗證”的嚴謹追求，還品味到“用發(fā)現(xiàn)的規(guī)律進行計算，能夠算得又對又快”的成功喜悅。顯然，多層次的聯(lián)系使得探索活動從低階邁上高階。

可以看出，多類型的舉例能夠較為全面地表征數(shù)學問題，不重復、不遺漏，探索結(jié)論就能避免以偏概全，實現(xiàn)以少勝多的高效學習。多角度的比較能夠為學生思考問題鋪路架橋，探索活動變得有方向、有方法，學生的思維質(zhì)量也就有了保障。多層次的聯(lián)系能夠做到基于數(shù)學問題，又超越具體問題，并最終使學生獲得一般意義上的良性發(fā)展。

二、實質(zhì)把握點睛，經(jīng)歷演繹算理

從探索的歷程來看，合情推理是探索活動的重要環(huán)節(jié)和必經(jīng)之路。考慮到學生的年齡特征、認知規(guī)律和知識特點，舉例、比較、聯(lián)系等方法的運用和內(nèi)化，在一定程度上仍能豐富和提升學生的數(shù)學素養(yǎng)。問題是，學習不能只有合情推理，還需要適時添加演繹推理，引導學生經(jīng)歷從“是什么”到“為什么”的思維跨越，逐步滲透理性精神。

1.表征梯度化

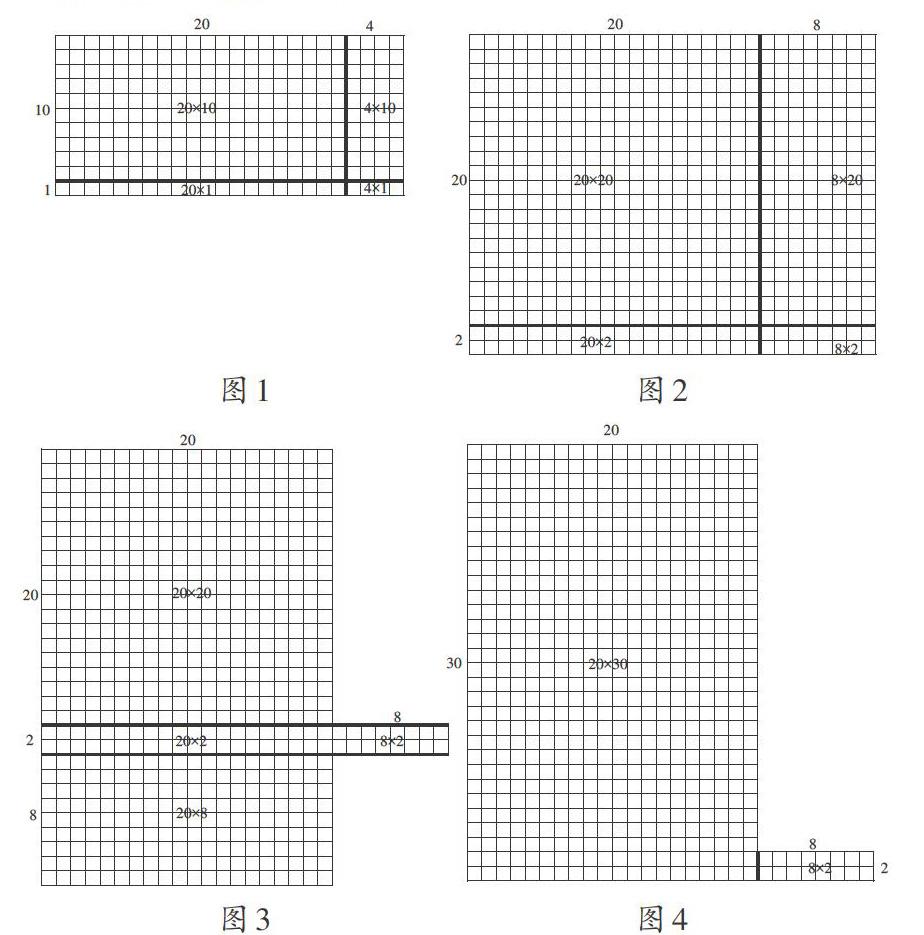
斯諾格拉斯的多水平模型認為，在不同的認知階段有不同層次的表征。首先，在知覺階段中，借助分類、列舉等活動，在初步感知表面特征的基礎(chǔ)上，鎖定“兩位數(shù)乘兩位數(shù)”計算中的特殊現(xiàn)象。其次，在工作記憶階段中，一方面借助言語表象表征，如用“兩頭一拉，中間相加”“滿十進一”描述“兩位數(shù)乘11”的計算規(guī)律，用“乘數(shù)個位上的數(shù)相乘的結(jié)果寫在積的末兩位（不足兩位的，用“0”在積的十位上占位），乘數(shù)十位上的數(shù)相乘的結(jié)果寫在積的末兩位前面”描述“同頭尾合十”的計算規(guī)律，等等;另一方面借助視覺表象表征，將所思所想用合適的圖式“可視化”，如“24×11”的計算過程如圖1所示，其中，4×1等于4，4就寫在積的個位上，4×10和20×1合起來等于60，6就寫在積的十位上，20×10等于200，2就寫在積的百位上，三部分合起來就是264;“28×22”的計算過程如圖2所示，將“20個8相加”看成“8個20相加”，并與“2個20相加”合并成“10個20相加”（如圖3），最后“8×2”的乘積16，恰好落在積的末兩位，“20×30”的乘積600，6就寫在百位上，兩部分合起來就是616（如圖4）。其實，還可以借助直觀圖形將“20×30”動態(tài)解構(gòu)成“2×（2+1）×100”的形式，并逐步抽象成“形如a（a+1）×100”的數(shù)學模型，有效消融學習的難點、盲點和困惑點。最后，在長時記憶階段中，雖然規(guī)律沒有用命題形式表征，但是有了前面的豐富經(jīng)歷，與探索相關(guān)的知識方法、過程體驗和情感態(tài)度逐漸變得明朗化，學習變得有滋有味、難以忘記。顯然，梯度化的表征相輔相成、相得益彰，為探明規(guī)律實質(zhì)奠定基礎(chǔ)。

2.反思體系化

反思不僅可以發(fā)生在板塊知識之內(nèi)，而且可以發(fā)生在板塊知識之間，甚至是超越知識本身獲得探索過程的深度理解。首先，從知識層面來反思，聯(lián)系上面的直觀圖形，先以“24×11”為例，可以清楚地發(fā)現(xiàn)“兩頭一拉，中間相加”的實質(zhì)，就是個位上的兩個數(shù)相乘的結(jié)果對應(yīng)記錄在積的個位上，十位上的兩個數(shù)相乘的結(jié)果對應(yīng)記錄在百位上，積的十位上記錄的內(nèi)容是兩部分的和：一部分是個位上的數(shù)乘十位上的數(shù)的結(jié)果，另一部分是十位上的數(shù)乘個位上的數(shù)的結(jié)果;再以“28×22”為例，與“24×11”不同的主要是在十位上，2×20+8×20=（2+8）×20=10×20，與百位上的20×20合并成10×20+20×20=（10+20）×20=30×20=600，這就是百位上記錄為“同頭的數(shù)×（同頭的數(shù)+1）”的真實原因，順著這樣的思路，十位空缺了，所以積的末兩位記錄的就是乘數(shù)個位上的數(shù)相乘的結(jié)果（不足兩位，用“0”占位）。換個角度來說，“兩位數(shù)乘兩位數(shù)”都必然發(fā)生四種運算：幾個×幾個=幾個（或十幾），幾個×幾十=幾十，幾十×幾個=幾十，幾十×幾十=幾百。其次，從方法層面來反思，無論是哪個版塊，都無一例外地經(jīng)歷了識別、發(fā)現(xiàn)、表達、驗證的過程，每一個過程都是探索的必要環(huán)節(jié)，比如“為什么要驗證？”，因為不完全歸納得到的結(jié)論不確定，以此需要“再多找一些例子試一試”或者“嘗試找出一些反例推翻猜想”，這樣的反思行為，使得每一個活動都“有理有據(jù)”，規(guī)定動作變?yōu)閮?nèi)在需求。顯然，體系化的反思使得看似不相關(guān)的知識得到整體建構(gòu)，看似規(guī)定的過程價值得以內(nèi)化，為探明規(guī)律實質(zhì)保駕護航。

3.遷移立體化

遷移是在把握規(guī)律實質(zhì)過程中的一種思維演練，既考查學生對規(guī)律本質(zhì)的理解情況，也檢驗學生運用規(guī)律的靈活程度。首先，基于知識類型和規(guī)律本身的遷移，比如“□5×□5=3025，3□×3□=1224，□□×□□=4209”，就是“同頭尾合十”的針對性訓練，這里特別強調(diào)積“24”的乘數(shù)組成、選擇和辨析，突出“尾合十”的實質(zhì)內(nèi)涵是“乘數(shù)個位上的數(shù)相加等于10”。其次，基于知識融合和規(guī)律交叉的遷移，比如“19×11”，既可以運用“兩位數(shù)乘11”的規(guī)律，也可以運用“同頭尾合十”的規(guī)律。接著，基于知識翻轉(zhuǎn)和規(guī)律變式的遷移，比如“34×74，25×85，41×61”，就是“同頭尾合十”的形式變換，即為“尾同頭合十”，鼓勵學生繼續(xù)探索并發(fā)現(xiàn)：尾乘尾，占兩位，放末尾;頭乘頭，再加尾，放前面。最后，基于知識延伸和規(guī)律同構(gòu)的遷移，比如“204×206”，探索內(nèi)容從兩位數(shù)走向三位數(shù)，數(shù)位雖然變多了，情況相對復雜了，但是探索規(guī)律的方法照舊，是知識解構(gòu)后的重構(gòu)。顯然，立體化的遷移不只是簡單機械地練習，還要更多地考慮探索方法的延續(xù)和內(nèi)化，考量知識的縱橫生長和發(fā)展，為探明規(guī)律實質(zhì)保值增效。

可以看出，探索過程中的經(jīng)歷是一種別樣美的風景線。教學就是要引導學生接觸、感知和理解規(guī)律美的存在，通過浸潤“是什么”的合情推理，自主建構(gòu)規(guī)律美的外在形式;還要能夠激發(fā)學生反思、剖析和把握規(guī)律美的內(nèi)在，通過浸潤“為什么”的演繹推理，共性刻畫規(guī)律美的內(nèi)在道理。顯然，合情合理的過程經(jīng)歷，能夠助推探索體驗“看得見”“說得通”和“帶得走”。

[本文系江蘇省教育科學“十三五”規(guī)劃重點課題“基于問題鏈驅(qū)動的小學生數(shù)學化學習的研究”階段性成果（課題批準文號：C-b/2020/02/26）。]

（責編 金 鈴）