設計問題鏈，助推學生思維發展

鄧曉琴

[摘 要]問題是數學課堂的重要組成部分。課堂上，教師對問題的設計直接影響著教學的質量。精心設計問題鏈，是實現高效課堂的重要方式。教師精心設計具有引導性、啟發性和探究性的問題鏈，不僅可以激發學生的問題意識，調動學生思考的主動性，還能提升學生的數學思維，讓數學知識更具魅力，讓數學課堂更加出彩。

[關鍵詞]問題鏈;引導;啟發;探究

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）11-0086-02

陶行知先生曾言：“發明千千萬，起點是一問。”課程標準指出，在關注學生主體地位的同時，不可忽視教師在課堂上的引導作用。問題鏈是一種新型的問題設計形式，是由一組問題或幾組問題組成的問題系統。問題鏈既包括教師在教學設計時預設的問題，又包含教師根據課堂的實際情況適時提出的問題。問題鏈中的問題環環相扣、步步深入，如同一根繩子將“珍珠寶石”串聯在一起。這些問題鏈對學生或引導，或啟發，將教學內容貫穿成一個整體。那么，教師在課堂上如何設計問題鏈，才能調動學生思考的主動性，落實學生對知識的深度學習呢？下面，筆者結合教學實踐做進一步探討，以期對廣大教育同仁提供有價值的參考和借鑒。

一、設計引導式問題鏈，啟動學生思維引擎

引導式問題鏈的主要作用在于引導，實現新知與舊知之間的無縫對接。因此，引導式問題鏈往往具有明顯的催動和引發作用。在設計引導式問題鏈時，教師要從學生的年齡特點和興趣偏好出發，把問題鏈和學生的實際生活聯系起來，進而營造輕松愉悅的學習氛圍，快速吸引學生注意力，使學生的思維自然過渡到對問題的思考中來。

【“分數的初步認識”教學節選】

師（問題1）：孫悟空去摘桃子，如果他摘了8個桃子，師徒4人要平均分，每人可以分到幾個桃子？

生1：這個問題應該用除法，8÷4=2（個）。

師（問題2）：如果孫悟空摘了4個桃子，師徒4人要平均分，每人可以分到幾個桃子？

生2：也是用除法計算，4÷4=1（個）。

師（問題3）：如果孫悟空只摘了2個桃子，師徒4人要平均分，每人可以分到幾個桃子？

生3：還是用除法計算，2÷4=……

生4：等于半個！

師（問題4）：那我們應該如何用數字來表示“半個”呢？

（學生討論）

師：在很多情況下，人們在進行分配的時候，發現每人分到的數并不一定是整數，要表示出這些“非整數”，也就是同學們剛才說的“半個”“半個多一點”“半個少一點”等情況，人們就發明了分數。現在，就讓我們認識這位“新朋友”吧！

小學生性格活潑好動，注意力集中的時間比較短，往往容易被一些新鮮、有趣的事物吸引。因此，教師在設計問題鏈時，要順應小學生的性格特點，把問題鏈置于生動有趣的情境之中。教學中，教師借助“分桃子”的生動情境引出問題鏈，在激發興趣的前提下引發學生主動思考。其中，問題1和問題2引導學生復習了整數的除法，而問題3和問題4則自然而然地將學生引入一個憑借現有知識難以解決的問題情境之中，從而引發思維沖突，使學生產生了一探究竟的強烈愿望。從整體上看，教師的問題鏈設計既起到了調動學生興趣的作用，又達成了“溫故而知新”的效果，不失為一次以問題鏈導入新課的成功嘗試。

二、設計啟發式問題鏈，誘導學生思維發展

子曰：“不憤不啟，不悱不發。”朱熹則進一步對此解釋道：“憤者，心求通而未得之意;悱者，口欲言而未能之貌。啟，謂開其意;發，謂達其辭。”由此可見，啟發主要強調教學的適度性和藝術性。因此，在教學中，教師要充分尊重學生的課堂主體地位，不可喧賓奪主。對于學生通過自主探究能夠解決的問題，教師不要過多干涉，更不要包辦代替，而是設計啟發式的問題鏈，通過問題對學生循循善誘，逐步引導學生思維發展，這樣既培養了學生自主思考、自主學習的能力，又能夠使學生更加深刻地理解知識。

【圓的面積知識點教學1】

師（問題1）：同學們，我們這節課學習“圓的面積”，你們認為可以通過哪些方法測得圓的面積呢？

生1：可以采用“數格子”的辦法。

生2：“數格子”的辦法比較麻煩，而且也不準確。

師（問題2）：看來要求出圓的面積，僅靠“數格子”的辦法還是不行。同學們還有更好的辦法嗎？

生3：可以通過我們已經學過的圖形的面積來推導。

師（問題3）：對，這是個好辦法。那么，我們都學過哪些圖形的面積呢？

生3：我們學過長方形、平行四邊形、三角形和梯形的面積。

師（問題4）：我們是如何推導這些圖形的面積的呢？

生4：求平行四邊形的面積是把它轉化為長方形;求三角形的面積是把它轉化為平行四邊形;求梯形的面積是把它轉化為平行四邊形。

師（問題5）：這些圖形的轉化過程都體現了什么數學思想方法？

生4：轉化思想。

師（問題6）：想一想，我們可以怎樣推導出圓的面積公式呢？

生5：可以采用轉化的方法。

生6：對，把圓轉化成我們學過的圖形。

生7：可以把圓轉化為平行四邊形試試。

……

“道而弗牽，強而弗抑，開而弗達”這句話告訴我們，要引導學生但決不牽著學生走;要嚴格要求學生，但決不使學生感到壓抑;要啟發點撥學生思考，決不能把答案直接和盤托出。設計啟發式問題鏈是引導學生思考，啟發學生思維發展的重要手段。上述教學中，教師為了引導學生通過“轉化思想”推導圓的面積，層層設問，使學生在對問題的解答中逐漸意識到新知與舊知的相通之處，由此自然而然地把思維聚焦到“轉化”的方法上來。值得指出的是，學生想到用“轉化”的辦法并非空想，而是教師精心設計問題鏈并有意識啟發學生思考的必然結果，這正凸顯了問題鏈在啟發學生思維方面的獨特優勢。

三、設計探究式問題鏈，推動學生思維深入

波利亞曾言 ，學習任何知識的最佳途徑是通過自己的實踐活動去發現，因為這樣的發現理解最深刻，也最容易掌握其中的內在規律、性質和聯系。探究是學生自主發現問題、解決問題的基本手段。教師設計具有開放性、指導性的探究式問題鏈，能夠啟發學生思考的方向，提升學生思考的維度和深度，從而不斷提升學生的探究能力和創新能力。在設計探究式問題鏈時，教師應注意從兩個方面把握：一方面是問題鏈的設計要精細化，由于探究式問題鏈是直接引導學生進行探究活動的，所以問題鏈的設計應明確、具體，這樣才能更好地指導學生進行數學探究;另一方面是問題鏈的設計要具有邏輯性，數學探究的過程既是一個行為過程，也是一個思維過程，具有明顯層次性和邏輯性的問題鏈，能使學生的探究思路更加清晰，有助于學生對知識獲得更加全面、精準的認識，從而把學生的思維推向深處。

【圓的面積知識點教學2】

師：我們已經明確要使用轉化的方法推導圓的面積，那么，請你們回答以下5個問題。

問題1：可以把圓轉化成什么圖形？

問題2：你是如何實現這種轉化的？

問題3：你是怎樣想到用這種轉化方法的？

問題4：轉化后的新圖形與圓之間有什么關系？

問題5：你這樣推導圓的面積公式的依據是什么？

（學生按照上述問題的順序，以小組為單位進行探究。教師巡回指導）

生1：我們小組把圓轉化成平行四邊形。

師：你能說一說你們是如何轉化的嗎？

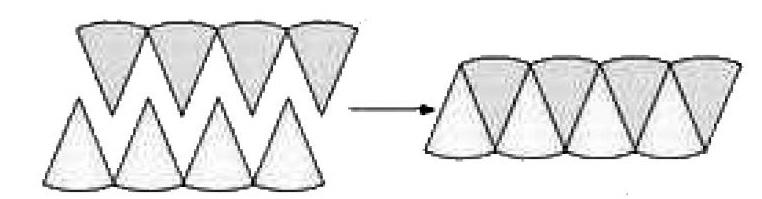
生1：我們把圓8等分，然后再把它們拼接起來（如下圖），這樣就把圓轉化成了平行四邊形。

師：你們是如何想到這種轉化方法的呢？

生2：一開始我們只想到了用“割補”法和“倍拼”法，但是我們發現這兩種方法都不能把圓轉化成學過的圖形。圓是一個曲面圖形，為了實現化曲為直，只能把圓分成多個等分，再拼接。

師：平行四邊形與圓之間有什么對應關系？

生3：這兩個圖形形狀不同，但面積一樣。其中，平行四邊形的底相當于圓的周長的一半，平行四邊形的高相當于圓的半徑，圓的面積=平行四邊形的面積=底×高=2πr÷2×r=πr2。

探究式問題鏈具有環環相扣、層層遞進的特點，能夠有效促進學生的思維向深度和廣度發展。上述教學中，教師為了更好地引導學生參與探究活動，用5個問題組成了一個具有明顯遞進性和邏輯性的問題鏈，這5個問題猶如學生數學探究的行動“手冊”和思維“指南”，學生按照教師提出的問題逐個探究、解答，最后“ 撥開云霧見明月”，收獲了真知，提升了探究能力，促進了思維的深入發展。

格蘭特·威金斯博士曾言，現代課程的基本單位是“問題”，課程改革的主要任務是“重新組織”課程，通過問題設計來組織課程內容，最終借助課堂教學加以解決問題。對問題的設計是數學教學不可或缺的重要環節。在教學中，教師精心設計問題鏈，其效應不僅僅表現為課堂教學效果的提升，更為重要的是對學生如何在學習中發現問題、提出問題、研究問題、解決問題起著潛移默化的影響。如此，學生的思維方法、思維能力、創新精神才能得到不斷訓練與增強，逐漸從“學會”走向“會學”。

（責編 覃小慧）