新型冠狀病毒傳播的數學模型研究綜述

王雨 孟鳳娟 施俊 王昊杰 董雯

摘要：以新型冠狀病毒的傳播作為研究對象，通過文獻查閱的方式對病毒的傳播機制進行了研究，查找并梳理了研究新型冠狀病毒傳播的相關模型，傳播動力學模型和基于時變參數的模型;總結了在不同因素作用下各模型的改進，多倉室因素下的傳染病動力學模型、多時段動態時滯動力學模型、考慮社交隔離的SEIRS模型和引入隱形傳播者的SEIR模型;最后，結合近期研究的離散模型，介紹了數據擬合的方法在離散模型中的應用，并說明數學模型對疫情防控的重要指導作用。

關鍵詞：新型冠狀病毒;數學模型;傳播動力學模型;時變參數;

中圖分類號：O242.1文獻標識碼：A文章編號：2095-7394（2021）06-0089-08

新型冠狀病毒肺炎疫情自2019年暴發至今，仍在全球多個國家和地區肆虐。除生物醫藥、衛生醫療等直接服務于疫情控制的學科和行業外，其他學科的學者也在運用專業知識積極投身于這場全球疫情阻擊戰。在病毒傳播階段，用合適的數學模型可以分析和預測其發展態勢，從而為各種防疫措施提供有效參考。當前，對新型冠狀病毒傳播進行分析預測的數學模型大體可以分為兩類：一類是運用傳播動力學模型（SIR模型、SEIR模型）對疫情的傳播建模;另一類是基于時變參數的數學模型（一般增長模型、Logistic模型）對現有數據的擬合。此外，也有學者通過引入新的參數或將兩類模型結合，從而提出新的思路與見解。

1傳統模型的改進

1.1傳播動力學模型

1.1.1SIR模型

SIR模型是最為普遍的數學模型，其基本思想是將所有人分為3種：易感者S，代表未被感染且不具有免疫力的群體;感染者I，代表具有一定傳染力的群體;移除者R，表示隔離、死亡及治愈且具有免疫力的群體，這部分人已退出傳染系統。這三類群體會以一定的概率發生狀態轉移，從而形成了“易感態—感染態—康復態”的動力學模型，如式（1）所示：

其中，N為人口總數，β為感染者與易感染者的接觸傳染率，γ為感染者被治愈速率。

喻孜等人[1]認為，此次的新型冠狀病毒傳播相比曾暴發過的SARS、MERS冠狀病毒有特殊之處，主要表現在總人口數的穩定性、人口流動因素（非封閉性）、隔離措施、潛伏期因素和初期的診斷能力等幾個方面。所以，SIR模型在運用方面有一定局限性，需要根據疫情發展的實際情況進行合理地修正。

1.1.2SEIR模型

SEIR模型以SIR模型為基礎，考慮了傳染病的潛伏期因素，且假定潛伏期內患者不具有傳染力。萬時雨等人[2]認為，新型冠狀病毒在潛伏期就具有傳染性，因此SEIR模型不能很好地模擬新型冠狀病毒的傳播趨勢。因此，學者們根據新型冠狀病毒的傳播特征，對SEIR模型進行了改良。Musa Salihu S.等人[3]認為，對輕度和重度病例采取不同的隔離措施，對疫情傳播發展具有重大影響，于是在SEIR模型中考慮了輕癥和重癥的隔離因素。朱翌民等人[4]認為，針對不同類型的感染者所需的防控措施應有所不同，因此考慮了隔離措施和潛伏期感染者的特點，改進了SEIR模型，在原有的四類群體中加入了被隔離的患者。李棟等人[5]認為，此次的新型冠狀病毒在潛伏期具有較強的感染能力，無法用SEIR模型描繪，于是構建了具有更好靈活性的SISR模型。

1.2基于時變參數的模型

如果不考慮新型冠狀病毒的傳播機制，而直接從數據入手進行擬合，則擬合效果與真實情況穩合度一般不高。張琳[6]假設感染人數的增長率會隨著累計感染人數的變化而變化，然后再把這個變化的函數關系帶入感染人數增長的微分方程，并擬合少量參數。

1.2.1一般增長模型

在新型冠狀病毒傳播初期，因為傳播的約束性較低，因而累計確診人數通常呈指數型增長，見式（2）：

y′（t）=ry（t）。（2）

張琳[6]認為，在很多已經暴發的傳染病中，相比于指數增長，次指數增長趨勢在疫情傳播初期更為常見，如HIV/AIDS、埃博拉和手足口病等;通過引入可調參數p（增長率的負加速度參數），得到預測累計感染人數的一般增長模型，見式（3）：

y′（t）=ry（t）^p。（3）

通過對疫情發展關鍵時間節點的劃分，全國新冠肺炎累計確診病例數的擬合可分為三個階段。在這三個階段中，由方程（3）分別擬合參數r、p，可通過查詢某日累計確診病例數得到初期感染人數y₀。

1.2.2Logistic模型

Logistic模型最初用來模擬種群變化，但該模型同樣也可模擬傳染病的增長趨勢。劉勝等人[7]認為，該模型主要分為加速上升和減速上升至不變兩個階段，充分反映了傳染病中病毒傳播特性與人為干預對感染的影響，因此，Logistic模型能很好地描述新型冠狀病毒的傳播規律。

但Logistic模型只能預測累計感染人數，對現有確診人數則無法做到模擬。馮苗勝等人[8]在Logistic模型的基礎上，綜合考慮到SEIR模型可以模擬傳染病傳播過程中各類人群數量的變化，于是對相關參數進行了調整，提出Logistic與SEIR結合的模型;該模型既克服了Logistic模型不能預測確診人數的缺點，也克服了SEIR模型調參太多的缺點。

2考慮特殊因素的改進數學模型

2.1多倉室因素下的傳染病動力學模型

作為研究傳染病傳播機理的定量方法，動力學模型的發展有著舉足輕重的作用。學者們通常以SIR、SEIR模型作為基礎，構建基于某種傳染病傳播特點及防控措施的傳染病模型。

桑茂盛等人[9]在倉室傳染病模型的基礎上，考慮到新冠病毒的特征及其傳播特點，綜合新冠疫情中潛伏期的隔離情況、感染者癥狀的顯隱性等分類，建立了一種新傳染病模型;結合COVID-19的傳播特點，作出如下基本假設：（1）新冠病毒感染者中有一部分無癥狀感染者，具備傳染性，無癥狀感染者不計入確診病例且經過發病周期后自愈;（2）新冠病毒肺炎存在潛伏期，潛伏期的病毒攜帶者具有傳染性卻沒有病征;（3）新冠病毒有變異的可能，治愈者具備一定時間的免疫周期，超過免疫周期之后再次感染率較小;（4）感染者在醫院里治療時，有感染醫護人員的可能，但傳染的比率較小。

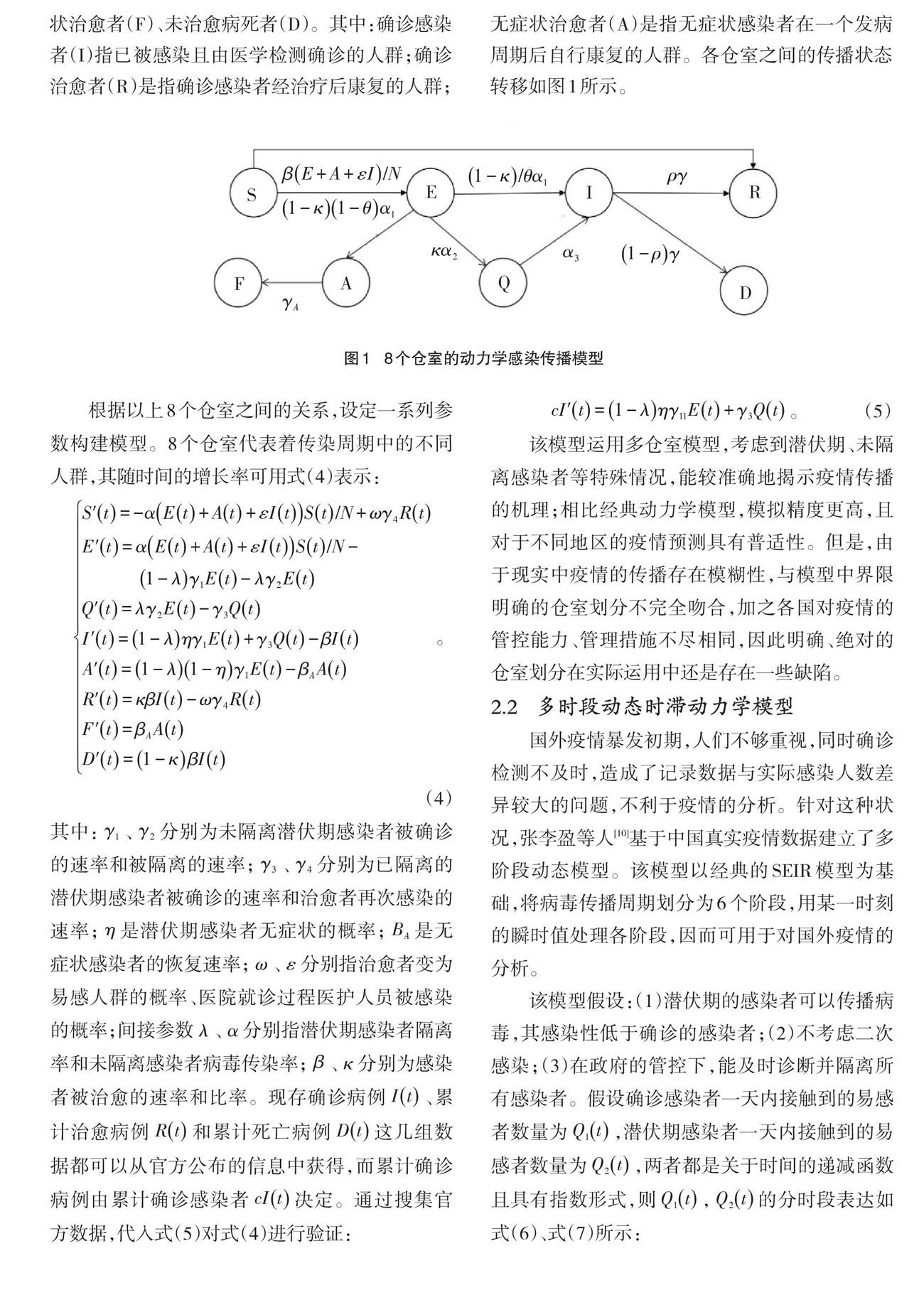
該模型建立了8個倉室：易感染者（S）、未隔離潛伏感染者（E）、已隔離潛伏感染者（Q）、確診感染者⑴、無癥狀感染者（A）、確診治愈者（R）、無癥狀治愈者（F）、未治愈病死者（D）。其中：確診感染者（I）指已被感染且由醫學檢測確診的人群;確診治愈者（R）是指確診感染者經治療后康復的人群;無癥狀治愈者（A）是指無癥狀感染者在一個發病周期后自行康復的人群。各倉室之間的傳播狀態轉移如圖1所示。

根據以上8個倉室之間的關系，設定一系列參數構建模型。8個倉室代表著傳染周期中的不同人群，其隨時間的增長率可用式（4）表示：

其中：γ₁、γ₂分別為未隔離潛伏期感染者被確診的速率和被隔離的速率;γ₃、γ₄分別為已隔離的潛伏期感染者被確診的速率和治愈者再次感染的速率;η是潛伏期感染者無癥狀的概率;B_A是無癥狀感染者的恢復速率;ω、ε分別指治愈者變為易感人群的概率、醫院就診過程醫護人員被感染的概率;間接參數λ、α分別指潛伏期感染者隔離率和未隔離感染者病毒傳染率;β、κ分別為感染者被治愈的速率和比率。現存確診病例I（t）、累計治愈病例R（t）和累計死亡病例D（t）這幾組數據都可以從官方公布的信息中獲得，而累計確診病例由累計確診感染者cI（t）決定。通過搜集官方數據，代入式（5）對式（4）進行驗證：

cI′（t）=（1-λ）ηγ₁₁E（t）+γ₃Q（t）。（5）

該模型運用多倉室模型，考慮到潛伏期、未隔離感染者等特殊情況，能較準確地揭示疫情傳播的機理;相比經典動力學模型，模擬精度更高，且對于不同地區的疫情預測具有普適性。但是，由于現實中疫情的傳播存在模糊性，與模型中界限明確的倉室劃分不完全吻合，加之各國對疫情的管控能力、管理措施不盡相同，因此明確、絕對的倉室劃分在實際運用中還是存在一些缺陷。

2.2多時段動態時滯動力學模型

國外疫情暴發初期，人們不夠重視，同時確診檢測不及時，造成了記錄數據與實際感染人數差異較大的問題，不利于疫情的分析。針對這種狀況，張李盈等人[10]基于中國真實疫情數據建立了多階段動態模型。該模型以經典的SEIR模型為基礎，將病毒傳播周期劃分為6個階段，用某一時刻的瞬時值處理各階段，因而可用于對國外疫情的分析。

該模型假設：（1）潛伏期的感染者可以傳播病毒，其感染性低于確診的感染者;（2）不考慮二次感染;（3）在政府的管控下，能及時診斷并隔離所有感染者。假設確診感染者一天內接觸到的易感者數量為Q₁（t），潛伏期感染者一天內接觸到的易感者數量為Q₂（t），兩者都是關于時間的遞減函數且具有指數形式，則Q₁（t），Q₂（t）的分時段表達如式（6）、式（7）所示：

其中：n₁、n′₁分別代表第一階段確診感染者和潛伏期感染者每天接觸到的易感者人數;n₂、n₃分別代表第二階段、第二階段后期確診感染者每天接觸到的易感者最小值;n'2、n'3分別代表第二階段、第二階段后期潛伏期感染者每天接觸到的易感者最小值;κ₁、κ₂分別代表階段二、階段三確診者的指數遞減速率;κ′₁、κ′₂分別代表階段二、階段三潛伏期感染者的指數遞減速率。

不同階段的疫情傳播狀況和政策實施決定感染者的有效接觸率，根據以上不同時段的傳播特征參數，有模型（8）：

其中，α_1i、α_2m（i=1，2，3;m=1，2，3）分別指確診感染者、潛伏期感染者每天接觸易感者數量，β_1j、β_2n（j=1，2，3;n =1，2，3）分別指不同時期易感者接觸確診感染者、潛伏期感染者的概率。式（6）和式（7）的區別在于，不同疫情防控階段對應的系數α_1i、α_2m、β_1j、β_2n不同：第一階段為暴發初期，設定確診感染者的傳染率為β₁₁，有效接觸人數為α₁₁，潛伏期感染者的傳染率為β₂₁，有效接觸人數為α₂₁;第二階段為隔離政策下的傳播期，由于政策的有力實施，感染者接觸健康人群使其感染的概率降低，其中潛伏感染者和確診感染者的有效接觸率分別為β₁₂，β₂₂;第三階段為緊急預防期，由于上一階段政策的實施，隔離力度加大，感染者的接觸率降低，潛伏感染者和確診感染者的有效接觸率分別為β₁₃、β₂₃;第四階段為強烈干預期，這一階段的隔離力度沒有改變，但隨著潛伏期的過渡，感染者的人數達到峰值，感染系數不變;第五階段為緩和期，緩和期的醫療資源得到一定的保障，感染人數的下降和治愈率的提高使疫情的傳播及預防控制的形勢得到改善，此時易感者接觸確診感染者和潛伏感染者的分別為α₁₂、α₂₂;第六階段為相持期，感染人數快速下降，各方面表現均為緩和期的優化，易感者接觸確診感染者和潛伏感染者的分別為α₁₃、α₂₃。

上述模型運用離散時間的方法，改進了多時滯動力學模型，刻畫了不同疫情防控階段的疫情傳播情況，適用于對各國新冠疫情傳播過程的模擬。但該模型未考慮境外輸入等人員流動情況，在疫情進入第六個階段或者一個周期結束后，將可能迎來下一個周期，此時的病毒往往會發生變異，如德爾塔病毒，因此模型還需在考慮外界因素的基礎上進行不斷優化。

2.3滾動SEIR模型

在疫情傳播過程中，人們會經歷從“不重視”到“自我保護”兩個階段。第一階段的基本再生數可認為是經典SEIR模型中的常數，第二階段各種防治措施開始完善、自我保護意識增強，使得基本再生數有所下降，所以第二階段的基本再生數是一個關于時間t的函數。

由此，謝家榮等人[11]提出了一種基本再生數會變化的SEIR模型，即滾動SEIR模型，見式（9）：

用計算機算法求解，即可預測出確診人數。

該模型在經典的SEIR模型基礎上通過變化基本再生數這個參數，能夠對某一國家或地區在人群采取自我保護措施后感染人數的預測起到重要作用。但是，該模型未考慮時間滯后性（檢測能力和醫療狀況能力不充足導致的時間差異）、輸出病例對其他城市的影響等因素，因此也存在一些局限性。

2.4考慮社交隔離的SEIRS模型

由于潛伏者和治愈者均存在二次感染的可能，社交隔離是有效控制疫情傳播的手段之一。為此，黃夢瑤等人[12]提出研究模型應該按照“S—E—I—R—S”的順序進行，基于不同的社交隔離方案會對疫情變化產生不同影響的認識，將隔離時間、隔離程度等因素引入模型。

該模型在4類基本人群的基礎上，將感染者進一步細化為非住院患者、住院非重癥患者和住院重癥患者。鑒于不同國家的醫療狀況和人口規模對疫情變化發展的不同作用，該模型選取了具有一定代表性的國家，如德國、中國、美國和印度的數據，對傳統的SEIRS模型參數進行了改進：（1）非重癥患者向康復者的轉化速率用δ_H表示;（2）未來重癥住院患者向重癥患者的轉化速率用δ_c表示;（3）重癥患者向康復者的轉化速率用ξ_H表示。

一般而言，醫療狀況較好的國家，如德國，δ_H會更大、δ_c會更小、ξ_H會更大;而對于醫療物資匱乏、醫務人員缺乏的國家，如印度，這三個參數則會相反;對于中國、美國這類國家，這三個參數則不做調整。因此，三個參數的取值見表1。同時，需要考慮不同國家疾病傳染率的最大值R_0max和死亡率α，這兩個值根據各國公布的數據分析得出，見表2。

該模型假設：以上4個國家從同一起始時間暴發疫情，且有相同的初始現有確診人數、潛伏人數和康復人數;考慮到各個國家對此次疫情的重視程度以及實施社交隔離的時間，將中國和印度設置為發現病例兩周后開始隔離，德國和美國設置為發現病例四周后開始隔離;在不同隔離時間的隔離方案中，設置多種不同隔離程度（隔離人數占總人數的百分比）來擬合各個國家的確診人數，以此體現不同國家的防疫效果。

通過該模型的研究發現，短期（時間≤12月）或長期（時間>12月）隔離在人口總數和醫療狀況不同的國家效果差異明顯。短期社交隔離時：時間超過6個月、程度小于50%的隔離方案對醫療狀況好、人口總數少的國家效果較好;時間短于6個月、程度大于50%的隔離方案對醫療狀況差、人口數多的國家效果較好。長期社交隔離時，時間越長、程度為50%的隔離方案防控效果最好。該模型從隔離時間、隔離程度、國情等多方面進行分析，能夠為后疫情時代各國防疫措施的改進提供參考，但也存在未考慮各國防疫方案的調整及不同隔離程度、隔離場景的區別等因素。

2.5引入隱形傳播者的SEIR模型

大部分的新型冠狀病毒傳播數學模型沒有考慮“隱形傳播者”，即那些攜帶病毒而未被進行隔離或醫學觀察，仍能傳播易感者的人。為此，林俊峰[13]在傳統SEIR模型的基礎上引入隱形傳播者要素，并修改相關定義，在預測和數據擬合上收到了很好的效果。相關修改和假設如下：（1）修改潛伏者（E）為有可疑跡象;（2）修改感染者⑴為潛伏者中被確診并被醫院隔離治療的人群;（3）引人隱形傳播者（U）;（4）隱形傳播者和潛伏者的傳播率恒定;（5）治愈率和死亡率是時間的函數;（6）忽略被隔離14天后未顯示出癥狀的病毒攜帶者。于是，得到的SEIR示意圖，見圖2;建立相應的微分方程，見式（11）：

式中：λ₁、λ₂分別表示一位潛伏者在單位時間內將易感者變為潛伏者的人數，以及一位隱形傳播者在單位時間內將易感者變為潛伏者的人數;p₁、p₂、p₃分別表示攜帶病毒的潛伏者在所有潛伏者中的占比、發現隱形傳播者的概率和攜帶病毒的潛伏者在單位時間中轉為感染者的概率;p_c，t和P_D，t分別表示第t天新增出院人數、新增死亡人數占前一天感染者的比例;治愈率P_c和死亡率P_D用統計數據采用冪函數進行擬合得出。考慮離散變化情形，將上述微分方程轉為差分方程，求解差分方程即可預測出相關人數。

該模型指出了隱形傳播者和留醫觀察人員的區別，適用于擬合疫情早期的情形，在預測和數據擬合上精度較高;隨著時間的增長，后期擬合精度有所下降，可采用分段擬合改進模型。總體上，引人隱形傳播者的SEIR模型比傳統的SEIR模型對研究疫情傳播更具有優越性。

3基于數據擬合的離散模型

隨著經濟的發展，國家內部及國家之間人口流動性加強，使得病毒傳播也變得愈加復雜，因此傳統動力學模型的預測效果有所下降。隨著人工智能和計算機模擬技術的快速發展，有學者開始利用人工智能算法直接對新冠病毒傳播的數據本身進行擬合。疫情初期，指數模型在評估預測中有著重要作用，而金啟軒[14]認為由于本次疫情的中間宿主和傳播路徑并未確定，無法取得確切的量化結果，所以在此基礎上建立的指數模型可信度也較低。于是，其對2020年1月23日之后的增長率進行了統計與建模，發現2020年2月4日之后的增長率變化與前幾天的變化有所不同，故從2月4日起進行數據擬合;令天數為t，得到線性回歸方程（12）：

增長率=15.37%-0.84%t，（12）

該模型所預測的結果與真實數據高度吻合。

同樣地，ZHAO等人[15]基于傳染病疫情報告率調整病例總數，使用均值7.5、標準差3.4的Gamma分布估計序列間隔，并且依據非線性最小二乘法來擬合指數增長的模型。JUNG等人[16]通過馬爾可夫鏈蒙特卡洛方法（MCMC）擬合指數增長模型，并且根據擬合的參數計算再生數。LAI等人[17]根據全球共享所有的流感數據倡議，對提供的52 個SARS-CoV-2基因組進行了分析，由指數增長率計算，從而擬合了指數增長模型。

在傳統倉室模型的基礎上改進得到的新模型，盡管可以較好地模擬疫情發展情況，但由于模型涉及的參數較多，且部分參數來源于以往的文獻，所以在一定程度上會造成模擬結果的偏差。DANILO等人的直接從意大利隆巴迪大區疫情暴發早期的每日新增數據人手，用泊松分布對數據進行擬合，較好地模擬了暴發早期的流行特征。ZHAO等人[19]運用SARS與MERS的平均代際間隔，估計了SARS-CoV2的代際間隔，使用泊松檢驗的對數似然法估計指數增長率，基于指數泊松過程擬合了疫情發展曲線。

引入時變參數，從數據方面直接入手，短期內進行預測的精度會明顯高于固定參數或者無機制模型的擬合方法，但對于長期的預測效果則不太理想。如果能建立多階段模型，不同傳播階段用不同的參數進行擬合，那么其長期預測和短期預測的準確性都會得到提高。

在人類與傳染病的斗爭中，數學模型發揮著越來越重要的作用。科學合理的數學模型，可為疫情的科學防控提供一定的理論依據。

參考文獻：

[1]喻孜，張貴清，劉慶珍，等.基于時變參數-SIR模型的COVID-19疫情評估和預測[J].電子科技大學學報，2020，49⑶：357-361.

[2]萬時雨，劉玨，劉民.新型冠狀病毒基本再生數研究進展[J].科學通報，2020，65（22）：2334-2341.

[3] Musa Salihu S.，高道舟，趙時，等.不同隔離措施對中國武漢市早期階段的新型冠狀病毒傳播影響的機理建模研究[J].應用數學學報，2020，43（2）：350-364.

[4]朱翌民，黃勃，王忠震，等.隔離措施對COVID-19疫情控制的模型分析[J].武漢大學學報（理學版），2020，66（5）：442-450.

[5]李棟，白瑞瑞.新型冠狀病毒傳播仿真組合模型[J].統計與決策，2020，36（5）：5-10.

[6]張琳.新冠肺炎疫情傳播的一般增長模型擬合與預測[J].電子科技大學學報，2020，49（3）：345-348.

[7]劉勝，王書昌，修志龍.新型冠狀病毒肺炎的傳染動力學[J].病毒學報，2020，36（3）：355-364.

[8]馮苗勝，王連生，林文水.Logistic與SEIR結合模型預測新型冠狀病毒肺炎傳播規律[J].廈門大學學報（自然科學版），2020，59（6）：1041-1046.

[9]桑茂盛，丁一，包銘磊，等.基于新冠病毒特征及防控措施的傳播動力學模型[J].系統工程理論與實踐，2021，41（1）：124-133.

[10]張李盈，李東宸，任景莉.多階段動態時滯動力學模型的COVID-19傳播分析[J].武漢大學學報（信息科學版），2020，45⑸：658-666.

[11]謝家榮，孫嘉辰，劉迅，等.新型冠狀病毒傳播的數學模型與預測[J].科學通報，2020，65（22）：2348-2355.

[12]黃夢瑤，黃麗達，袁宏永，等.社交隔離對COVID-19的發展影響[J].清華大學學報（自然科學版），2021，61（2）：96-103.

[13]林俊鋒.基于引入隱形傳播者的SEIR模型的COVID- 19 疫情分析和預測[J].電子科技大學學報，2020，49（3）：375-382.

[14]金啟軒.中國新冠肺炎疫情預測建模與理性評估[J].統計與決策，2020，36（5）：11-14.

[15] ZHAO S，LINQY，RAN J J，et al. The basic reproduction number of novel coronavirus （2019- nCoV）estimation based on exponential growth in the early outbreak in China from 2019 to 2020：a reply to Dhungana[J]. International Journal of Infectious Diseases，2020，94：148-150.

[16] JUNG S M，AKHMETZHANOVAR，HAYASHI K，et al. Real-time estimation of the risk of death from novel coronavirus （COVID-19）infection：inference using exported cases[J]. medRxiv，2020. DOI：10.1101/2020.01.29.20019547.

[17] LAI A，BERGNA A，ACCIARRI C，et al. Early phylogenetic estimate of the effective reproduction number of SARS-CoV-2[J]. Journal of Medical Virology，2020，92 （6）：675-679.

[18] DANILO C，MATTIA M，MARCELLO T，et al. The early phase of the COVID- 19 outbreak in Lombardy，Italy[J]. Epidemics，2021，37：100528.doi：10.1016/J.EPIDEM.2021.100528.

[19] ZHAO S，MUSA SS，LINQY，et al. Estimating the unreported number of novel coronavirus（2019-nCoV）cases in China in the first half of January 2020：a data-driven modelling analysis of the early outbreak[J]. Journal of Clinical Medicine，2020，9（2）：388.

A Review of Mathematical Models for Novel Coronavirus Transmission

WANG Yu，MENG Fengjuan，SHI Jun，WANG Haojie，DONG Wen

（School of Mathematics and Physics，Jiangsu University of Technology，Changzhou 213001，China）

Abstract：In this paper，the transmission of novel coronavirus is taken as the research object，and the transmission mechanism of the virus is studied through literature review. Relevant models for the study of novel coronavirus transmission are searched and sorted out：transmission dynamics model and time-varying parameter model. Then，the improvement of the models under the effect of different factors is summarized：the infectious disease dynamics model under the multi- compartment factor，the multi-time dynamic time- delay dynamics model，the SEIRS model with social isolation and the SEIR model with invisible communicators. Finally，the application of the data fitting method in the discrete model is introduced based on the discrete model recently studied，and the important guiding role of the mathematical model in epidemic prevention and control is illustrated.

Key words：novel coronavirus;mathematical model;propagation dynamics model;time-varying parameters