實踐探索，行而得知

程健

摘要：實踐探索是數學課堂教學中常用的一種學習方式。 以五年級下冊"解決問題的策略一一轉化” 一課為例展開研究，發現實踐探索對于數學思維的發展、數學思想的培養、數學方法的形成和數學知識的生成都有著重要的促進作用。

關鍵詞：實踐探索;數學思想;轉化策略

陶行知先生曾說過：“行是知之始，認識來源于實 踐，實踐是認識的基礎。”“實踐探索”是近年來廣受 師生喜愛的一種學習方式，這種方式融學生的觀察、操 作、思考于一體，是一種具身的認知活動。孩子們通過 動手、動腦、動口等多方位的實踐活動，參與數學知識 的探索過程，充分體驗和感悟數學知識的形成，在此過 程中反復經歷多次提出問題、解決問題的過程，對知識 的形成有了更全面的掌握。下面，筆者就執教的五年級 下冊"解決問題的策略一轉化” 一課，談談“實踐探 索”在教學中的實施與感受。

一、實踐探索促進數學思維的發展

匈牙利數學家波利亞說："數學既是一門系統性的 演繹科學，也是一種實驗性的歸納科學。”毋庸置疑， 實踐探索能讓學生在做中學、學中思，“學思創共生”。 但是，實踐探索不同于數學操作，數學操作是學生動手 能力的體現。在實際教學中，許多老師把實踐探索和數 學操作混為一談，將兩者等同起來，學生在實踐探索中 往往淪落為一個"操作工人”，只停留在動手操作中， 而失去了對問題的思考。實踐探索不僅僅體現為學生的 動手能力，更為重要的是學生思維能力的體現，所以實踐探索可以說是一種"具身認知”。

案例1：教學例1，突出轉化優勢。

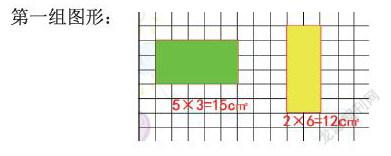
（1）比較兩個圖形的面積。（長方形）

第一組圖形：

說說你是怎么比的？計算長方形的面積。

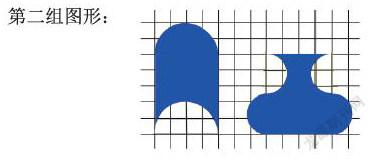
第二組圖形：

師：你能通過直接計算比較出這兩個圖形的面積大 小嗎？為什么？（圖形不規則了）猜猜哪個面積大？

師：你們有沒有好的辦法來比較這兩個圖形的面積 大小呢？小組合作探究。

（2） 合作探究。要求：小組合作探究，每組拿出下 發的小組合作單及兩個紙片模型，通過想一想、畫一畫、 剪_剪、拼一拼等方法比較兩個圖形的大小。學生動手， 教師巡視指導。

小組交流：說說你們組是怎么比較的。

預設：剪拼，學生演示剪拼的過程。

（3） 課件演示割補的過程，教師邊演示邊講解。講 解中突出平移和旋轉。（板書：平移、旋轉）

師：轉化成長方形就能比較出面積大小了。仔細觀 察一下，在轉化過程中，兩個圖形的什么變了，什么沒 變？（板書：形狀變了，面積不變）

師：這就是轉化方法中的一種常用方法一等積變 形。（板書：等積變形）

學生通過小組合作實踐探究來比較兩個不規則圖形 的面積，通過動手剪一剪、拼一拼等實踐活動，親身經 歷了問題的探究過程，明白可以運用平移、旋轉等方法 實現轉化。轉化的策略在學生的直觀操作中得到充分體 現，加深了學生對轉化策略的體驗。在這個實踐探索活動中，學生不僅有了動手操作的親身體驗，同時伴隨著 動手操作，學生的思維經歷了從“如何求不規則圖形面積“ 到"如何轉化成規則圖形"，再到"轉化前后兩個圖形 面積怎樣”等一系列發展過程，這才有了對轉化策略的 深刻理解，也突出了實踐探索對數學知識感性認識的重 要作用。

二、實踐探索促進數學思想的培養

《義務教育數學課程標準》在"實施建議”中指出： 數學思想蘊含在數學知識形成、發展和應用的過程中， 是數學知識和方法在更高層次上的抽象與概括。在課堂 教學中，教師在傳授數學知識的同時，更要滲透正確的 數學思想，培養學生解決生活實際問題的能力，讓他們 以不變應萬變，受益終身。王永春老師指出：“每一個 新知識都是在已有知識的基礎上發展的，要善于運用類 比推理和比較差異的思想方法進行新舊知識的轉化，達到 觸類旁通、方法遷移的目的。"因此，“轉化”就成了 一種重要的數學思想。

案例1：通過小組合作實踐探究，探索比較兩個不規則 圖形的面積，學生每組拿出下發的小組合作單及兩個紙 片模型，通過想一想、畫一畫、剪一剪、拼一拼等方法 比較兩個圖形的大小。各組學生都能想到把不規則圖形 轉化成規則圖形，但是，如何轉化是一個開放性過程， 尤其是第二個圖形。在交流時，筆者發現學生用了不同 的轉化方法。

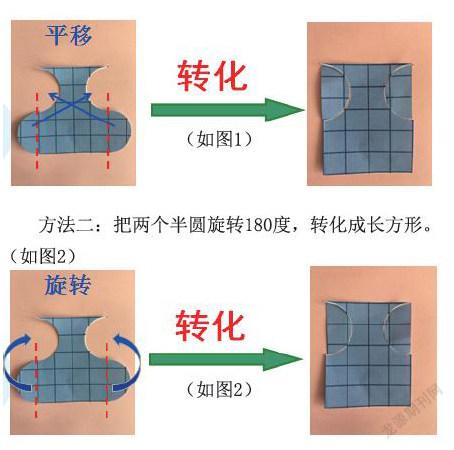
方法一：把兩個半圓分別通過兩次平移的方法，轉 化成長方形。（如圖1）

方法二：把兩個半圓旋轉180度，轉化成長方形。（如圖2）

方法三：把圖形沿中間對稱軸剪開，一半翻轉后拼 成長方形。（如圖3）

在合作實踐探究過程中，學生發揮各自的想法，釆 用多種方法將不規則圖形轉化成了長方形。這樣不僅讓 學生學會了用不同的方法來實現轉化，更幫助學生建立 和培養了 “轉化”的數學思想。在這一系列的動手實踐 活動中，學生充分感受知識實踐性的生成過程，由知識 催生方法，再由方法上升為思想，培養學生的轉化思想， 并能在解決實際問題中靈活運用。

三、實踐探索促進數學方法的形成

案例2：回顧、反思、小結。

師：剛才，我們通過平移和旋轉的方法把這兩個復 雜的圖形轉化成簡單的長方形，方便了我們比較。（板 書：復雜一簡單）下面讓我們來看看另外幾個圖形的面 積問題。（用分數表示各圖中的涂色部分）

師：我們再來看幾個圖形的面積問題。請你說說你 是怎么想的？最后的圖形如果擺正了，邊長是多少？

師小結：上面這些不規則圖形，我們同樣可以通過平 移、旋轉等方法把它們轉化成怎樣的圖形？規則圖形。 其實，就是把較復雜的問題轉化成了較簡單的問題。（板 書：不規則一規則）

學生通過實踐探索，親身經歷了通過平移、旋轉將 不規則圖形轉化為規則圖形的過程，在充分思考圖形轉 化策略的同時，也對圖形面積的轉化方法有了一定的積 累，平移、旋轉成了他們完成轉化的有效方法。形成了 特定的方法后，在接下來用分數表示涂色部分的面積的練 習中，學生有了明確的方法，知道運用轉化的策略解決 問題。對于最后一題，學生能發散出多種平移和旋轉的 方藻實現面積轉化，但是最后發現，無論哪一種撫， 其實都實現了把不規則轉化成規則圖形，使問題簡單化 To由此，學生經歷了從數學思想到數學方法、再由數 學方法回歸到數學思想的解決過程。

案例3：圖形周長。

師：圖形的面積問題可以通過平移、旋轉來轉化，那 圖形調整的周長問題可以轉化嗎？要求這個圖形的周長， 它是一個什么樣的圖形？你能指出它的周長嗎？周長好 求嗎？

師：你有什么辦法來求它的周長呢？

課件演示學生的想法：可以把豎直的線段怎么平移？ 橫的線段呢？

師：在這個轉化過程中，你又有什么變與不變的發 現呢？（板書：形狀變了，周長不變）我們也給這個轉 化起一個名字，叫“等長變形”。

師：周長計算中的轉化（練習十六1）。

（1） 格子圖中這個圖形的周長，你會求嗎？請你在 練習紙上畫一畫，并算出周長。

（2） 交流：說說你是怎么想的？（投影、課件演示） 延續著圖形的面積問題，圖形周長問題的研究同樣

從學生的實踐探索著手。在明確圖形周長的概念后，學 生有了對圖形周長的思考：“怎樣使這些線段圍成規則圖 形呢？ ”在問題的驅動下，學生產生了方法的遷移，他 們能想到通過平移線段的方法來轉化成規則圖形的周長。 在學生親身經歷了這樣的實踐探索后，再讓他們來看練 習十六的問題，學生更是明白了周長轉化的正確方法， 能用語言將方法精準歸納為“豎直線段左右平移，橫線 段上下平移”。當然，方法是為轉化策略服務的，但對 具體方法的掌握也是運用轉化策略解決問題能力的培養 和提高途徑。

因此，在教學時，教師在教會學生各種方法的同時， 更要幫助他們跳出這些具體方法，樹立轉化的數學思想， 通過數學思想讓他們的思維更寬廣。

四、實踐探索促進數學知識的生成

數學知識的學習是學生從具體逐步走向抽象的認知 發展過程，尤其是到了高年級，學生學習數學要釆用操 作、想象與推理相結合的方式來促進知識的生成。

案例4：回顧轉化實例，感受轉化的價值。

談話：同學們，其實"轉化”的策略并不神秘，我 們曾經在不知不覺中用到了許多。比如，在平行四邊形 面積公式的推導中，我們把平行四邊形轉化成長方形。 再如，計算除數是小數的除法時，我們利用商不變規律 轉化成除數是整數的除法。那么，在圖形和計算領域， 你還能想到哪些用到了轉化策略的內容呢？

（1） 小組回顧：小組合作進行整理，并寫在小組表 格里。教師引導學生先回顧圖形領域中運用的轉化策略， 再回顧計算及數與代數領域運用的轉化策略。

（2） 學生小組交流后匯報，結合課件演示。

圖形面積：平行四邊形、三角形、梯形、圓形的面 積推導。

周長、內角和：化曲為直求樹葉周長，把三角形三 個角轉化成平角求內角和

計算：小數乘法轉化為整數乘法、分數比較大小轉 化成小數、簡便計算。

（3） 小結：回顧和整理了這么多關于運用轉化策略 的例子，你有沒有發現這些運用轉化策略解決問題的過 程有什么共同點？

在經歷了圖形面積轉化和圖形周長轉化后，學生對 圖形轉化有了一定的理解，并逐步自主建立了轉化的概 念：轉化就是把復雜轉化為簡單，把不規則轉化為規則。 接著，教師介紹平行四邊形面積推導和除數是小數的除 法兩個例子，使學生產生推理思想，形成對轉化的進一 步理解，即轉化就是由一種形態轉化到另一種形態，充分 完善了轉化策略的內涵。然后，學生根據這一發現來歸 納用轉化策略解決過的數學問題，形成一種知識的歸納。 這樣從具體圖形問題抽象出數學策略，再由數學策略又 回歸到具體學過的數學知識，充分體現了數學知識的生 成過程，也體現了學習數學的價值意義。

實踐探索對于學生的思維發展，數學思想、方法的 形成，以及數學知識的生成，都有著十分重要的意義。 所以，在課堂教學中，教師要正確引導學生主動參與實 踐探索，初步學會先思考后操作、邊操作邊思考的探索 方法，鼓勵他們與別人分享和交流實踐探索的過程和成 果，不斷積累操作經驗，提高在實踐探索中學習數學的 能力。

參考文獻：

[1]鄭俊選.小學數學教學改革實踐與研究W].北京： 人民教育出版社，2003.

（責任編輯：吳延甲）