HPM視角下的數學教學設計：以坐標系為例

許紫晨 郭劉龍

摘 要：數學史和數學教育在國內外都受到了廣泛的關注，研究發展迅速。發生教學原理是數學教學研究的主要理論依據，考察歷史并進行歷史重構用于教學。研究以坐標系為例根據發生教學原理進行HPM視角下的教學設計，讓學生在學習坐標系的過程中，了解歷史上平面直角坐標系的發生發展，幫助學生穩固地建構數學知識體系，加強學生的數學思維。希望可以幫助學生以更廣闊的視角來看數學，增加學生對數學及其社會文化背景的領悟。

關鍵詞：HPM;坐標系;發生教學法;教學設計

坐標系作為數學中的一個重要工具，它架起了數與形的橋梁，構成了數形相互轉化的理論基礎。建立坐標系不僅是學習函數及其圖象、曲線和方程的前提，更起到了將幾何曲線和代數方程聯系起來的作用。對于學生來說，這一部分內容不是全新未接觸過的知識，在學習坐標系之前學生已經學習了數軸，所以平面直角坐標系是基于這一背景設置的一次概念教學。

如今，數學史和數學教育在國內外都受到了廣泛的關注，HPM的教學研究發展非常迅速，將數學史融入數學教學之后，課堂中的數學更加豐富，增強了趣味性，降低了數學學習的枯燥感。HPM教學開啟了多元教學方法之門，是幫助師生認識數學內部知識以及數學和其他學科之間聯系的良好手段，這在當今的數學教育改革中受到了高度的重視[1]。但目前數學史與數學課堂教學存在“高評價、低應用”的現實處境，在課堂教學中滲透數學史，激發學生的數學求知欲，幫助學生認識數學本質，同時使數學史展現數學價值，是HPM教學研究的重要部分，也是教師應該深入思考并為之努力的方向[2]。本研究選取初中數學中的平面直角坐標系這一章節內容，進行HPM視角下的教學設計研究。

本研究從HPM的視角進行教學設計，使學生經歷平面直角坐標系的形成過程，擬定了以下教學目標：（1）結合具體生活情境，體會可以用有序數表示物體的位置。（2）體會歷史上平面直角坐標系的發展過程，認識平面直角坐標系的概念，能畫出平面直角坐標系。（3）在給定的坐標系中，能根據坐標找出點的位置，可以根據點的位置寫出對應的坐標。（4）在實際問題中，能建立適當的坐標系解題。（5）在平面上，能用方位角和距離刻畫兩個物體的相對位置。

一、發生教學法

發生教學原理是數學教學研究的主要理論依據，提倡教師考察歷史，進行歷史重構，然后用于教學，引導學生發揮自身的主動性來學習新知識。

數學史在數學教學中的運用方式有三種：第一種是提供直接的歷史信息，這種僅講述數學歷史故事的方法比較淺層;第二種是借鑒歷史，重構歷史用于教學，將歷史重構重演，呈現出知識的自然發生過程，關注學生的學習動機，幫助學生提升認知能力;第三層次是開發學生對數學及其社會文化背景的深刻覺悟[3]，使學生在數學史的熏陶中更加喜歡數學。發生教學法屬于第二種方法，能更有效地使學生領悟數學文化。

1.發生教學法的起源

早在古希臘時期，亞里士多德就提出：兒童在發展過程中必須一個時期一個時期地重演人類從野蠻到文明的發展階段。此后一些教育學家如裴斯泰洛奇、弗羅貝爾均提出了發生教學的相關觀點。19世紀開始，人們更加關注發生教學，英國教育家斯賓塞這樣解釋發生教學：個體知識的發生是一定要遵循全人類知識的發生過程的，發生原理同時也受到生物學家生物發生基本定律的支持[4]。

“發生教學”這一概念最早由第斯多惠提出，他認為所有的學科都應進行“發生教學”，這既是學科興起的方式，又是進入人類意識的方式。

波利亞系統地敘述了發生原理：在教一門科學分支的理論或概念時，應當讓兒童重演人類心理演進的重大步驟。基于對重大步驟的解釋，波利亞提出了發生原理的更模糊的形式：只有深入地理解了歷史上人類是如何獲得某些事實或概念的，我們才能對人類的孩子現在應該如何獲得知識做出更好的判斷。

托普利茨明確了發生教學法的本質是追溯思想的歷史起源，尋找激發學習動機的最佳方式，通過研究前人所做工作的背景，來尋求他試圖回答的關鍵問題[5]。他的《微積分：發生的方法》一書的出版，標志著發生教學法在數學教學領域得到了普遍的一致的認可。

弗賴登塔爾認為發生教學重要的是歷史的“再創造”，教師應該借助歷史設計教學，引導學生回顧歷史上知識的創造，了解知識的形成、發展過程，讓學生在學習中通過自己的實踐與思考實現知識的再一次創造[6]。

從上面敘述可以看出，發生教學是一種借鑒歷史以呈現知識自然發生的過程的教學方法，教師應當基于歷史，借鑒或重構知識的發生發展過程。原本的歷史一般很復雜，發生法重構的歷史卻是線性的。發生法建立在學生的認知發展基礎上，強調知識的重要性，激發學生的學習動機。

2.發生教學法的應用

根據發生教學法進行教學設計，需要明確其重要步驟：（1）教師需要知道教學主題相關知識的歷史發展。（2）確定歷史發展過程中的關鍵環節。（3）判斷教學主題是否適用于發生教學法，如果適用于此方法，那么重構上面的關鍵環節，使歷史線性化適用于課堂教學。（4）設計出層層遞進的、由簡至繁的問題便于學生學習與思考。

二、坐標系的歷史

坐標幾何又稱解析幾何，借助坐標將平面上的點與有序數對進行一一對應的這種思想在最開始出現在古希臘和阿拉伯，阿波羅尼奧斯等科學家研究圓錐曲線時用到了這種思想。法國的數學家奧姆萊斯，他其實已經接觸到了函數的圖象表示：借用經度和緯度這兩個地理術語描述了他的圖線，實質上是現在的橫縱坐標。但是他未形成清晰的坐標概念，圖線概念是較為模糊的。法國的兩位數學家：勒內·笛卡爾（R.Descartes）和皮埃爾·費馬（P.de Fermat）[7]是解析幾何的最終發明者，他們雖然發明坐標系的初衷不同，但是殊途同歸，都提出了坐標思想。

1.笛卡爾與坐標系

（1）坐標系的誕生

笛卡爾發明解析幾何是為了研究著名的帕波斯問題。這一數學難題可以推廣到n條直線的情形。笛卡爾在證明四線問題的帕波斯結論時，嘗試建立坐標系：他選定了一條直線作為基線（這條基線相當于一條坐標軸），然后又選定一條線段，這條線段從基線出發，與基線形成了定角，這樣，歷史上第一個坐標系形成，這一坐標系為傾斜坐標系。坐標系不僅僅提供了解決作圖問題的新方法，笛卡爾巧妙地將代數方程和曲線、曲面進行聯系的這一創舉，也為他自己和后來的數學家提供了新的數學思考方向。

（2）笛卡爾創立坐標系的傳說

笛卡爾晚年生病臥床看見天花板上有一只蒼蠅在爬，于是思考如何將這只蒼蠅精準地進行定位。他認為可以將蒼蠅看成一個點，如果選定某點作為參考點，假設蒼蠅從參考點出發，需要數一下蒼蠅沿東西方向經過幾格天花板，沿南北方向經過幾格天花板，就能到達現在的點?？偨Y來說，在平面上需要選定一個參考點和兩個不重疊的方向來定位蒼蠅的位置，平面上任意一點的位置可以用有順序的兩個數表示。描述天花板上蒼蠅的位置是笛卡爾發明坐標系的最初靈感。

這個傳說還有另一個版本：笛卡爾看見的不是蒼蠅而是屋頂的一只蜘蛛，蜘蛛拉著絲上下左右運動。如何表示蜘蛛的位置呢？他想到可以把墻角頂點作為參考點，將屋子里相鄰的兩面墻與地面交出的三條線看作三個方向，也就是說，在空間中可以選定一個參考點和三個不重疊的方向來定位任意一點的位置，具體位置用三根數軸上的有順序的三個數表示。

2.費馬與坐標系

與笛卡爾不同，笛卡爾是用代數的方法研究幾何，而費馬的出發點是想要用幾何研究代數。費馬考慮任意曲線和它任意一點J，選取一條線作為底線，點J的位置可以用A、E兩字母確定，A表示從點O沿著底線到點Z的距離，E是從Z到J的距離，A和E對應著現在x軸和y軸，如圖1。他這樣做出的坐標，同笛卡爾一樣是傾斜坐標。在費馬的坐標系中y軸沒有明確的出現，也沒有考慮負數[8]。費馬在他的書《論平面和立體的軌跡引論》中闡述了解析幾何的原理，提出了坐標的概念，還使用了斜坐標系和直角坐標系。

3.坐標幾何的發展

笛卡爾和費馬的坐標系中橫、縱坐標軸都局限在正數，沒有考慮負坐標軸。

英國的數學家沃里斯是第一個有意識地引進負的橫、縱坐標的人，將坐標幾何從曲線的范圍拓展到了整個平面，同時他還為傳播坐標幾何的思想做出了巨大的貢獻。

后來，牛頓引入極坐標系和雙坐標系，極坐標系用一個固定的點和一條通過這一點的直線建立，雙坐標系每個點的位置決定了它到兩個固定點的距離[8]。17世紀中葉，坐標系又被推廣到三維空間乃至更高維空間。到18世紀，“解析幾何”慢慢地成為一門利用解析式研究幾何的幾何學分支。

三、坐標系的歷史重構

經過上面對數學歷史的考察，可以將坐標系的歷史分為五個環節。第一個環節是有序數對。第二個環節是單軸的建立：笛卡爾為了研究帕泊斯問題建立傾斜坐標系，費馬在研究方程的曲線時做出了傾斜坐標。他們都研究出了傾斜坐標，且坐標都局限在正數范圍。第三個環節是直角坐標系：笛卡爾在他的著作《方法論》的附錄《幾何學》第三卷中給出了直角坐標系，費馬在《論平面和立體的軌跡引論》（1629）一書中使用了直角坐標系。平面直角坐標系是現今常用的坐標系，使用量最多、最廣泛。牛頓引入極坐標系和雙坐標系，坐標系也被推廣到三維空間和更高維空間。第四個環節是負坐標引入：沃里斯引進負的橫、縱坐標，將坐標幾何從曲線的范圍拓展到了整個平面。第五個環節是坐標系的發展：極坐標系、雙坐標系、柱坐標系和球坐標系等被發明，解析幾何成為幾何學的一個分支學科。

教材通常是用以下的環節講解坐標系的知識：有序數對、數軸（單軸）、平面直角坐標系、坐標的應用。

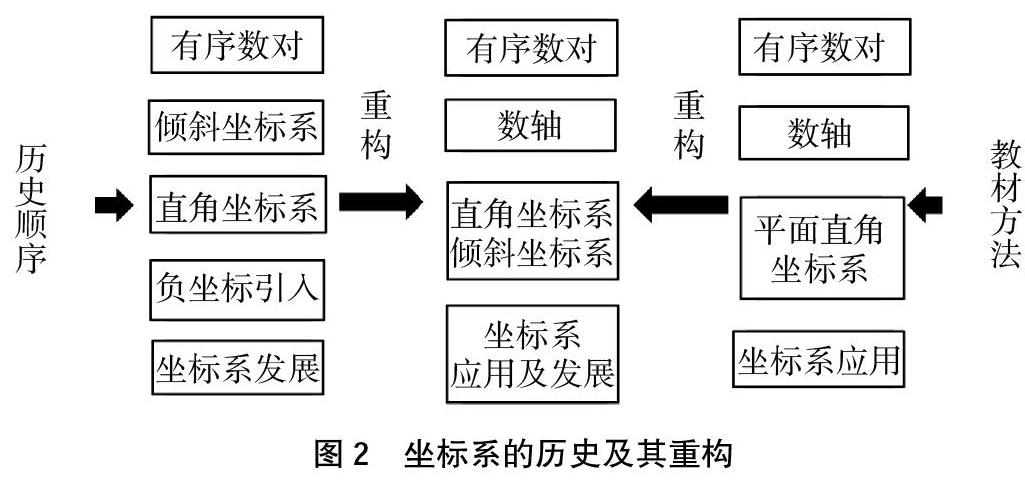
通過對比坐標系的歷史環節與教材中坐標系環節可以知道教材省略了傾斜坐標、負坐標引入、坐標系的發展環節，直接給出了平面直角坐標系的概念性定義，對照發生教學法，存在以下不足之處：（1）簡化了平面直角坐標系的歷史，沒有解釋在平面上畫兩條互相垂直、原點重合的數軸的緣由。（2）沒有讓學生了解到坐標軸有其他的類型，如傾斜坐標和極坐標，應當擴展學生對坐標軸的認知，激發學生的學習動機。為了適合教學，需要對其進行重構。下面用圖2表示坐標系的歷史及其重構。

四、坐標系的教學設計

1.有序數對

用去電影院看電影時尋找座位“幾排幾號”的情境和學生在教室中的位置“第幾行第幾列”的例子引出有序數對的相關概念。明確有序數對的定義。

2.數軸

復習數軸的相關知識時，強調幾個重要的知識：數軸的三要素為原點、正方向和單位長度;數軸上的點和實數的關系是一一對應關系;每一個實數都可以用數軸上的點來表示。

3.直角坐標系及傾斜坐標系

從學生學過的數軸入手，將坐標系的歷史融入故事中進行歷史重構，設計教學情境，向學生提出問題，引發學生的思考。

情境：法國著名數學家笛卡爾最早引入了坐標系，他采用代數的方法研究幾何圖形。笛卡爾晚年生病臥床，有一天，他看見天花板上有一只蒼蠅在慢慢爬動。笛卡爾想：如果我把這只蒼蠅看成一個點的話，那么蒼蠅的位置該如何表示呢？

問題1：這只蒼蠅向右爬了五個格，我們應該如何用數對表示蒼蠅的位置？問題2：這只蒼蠅向右爬了五個格，接著向左爬了七個格，我們應該如何用數對表示蒼蠅的位置？問題3：這只蒼蠅向上爬了五個格，我們應該如何用數對表示蒼蠅的位置？問題4：這只蒼蠅向右爬了五個格，接著向上爬了三個格，我們應該如何用數對表示蒼蠅的位置[9]？

學生在看到問題1和問題2后，在學習數軸的基礎上能較快聯系數軸，解決問題1和問題2是沒有困難的。問題3引導學生改變數軸方向：正方向從向右變成了向上，數軸從橫方向變成了縱方向。問題4的目的是引發學生的認知沖突，使學生注意到本題的數軸與上面問題中的數軸是有差異的，原來學習的數軸是一維層面上的，現在蒼蠅在一個平面上行走，我們現在要表示的是蒼蠅在平面上的位置。學生可以想到用有序數對來表示蒼蠅的位置。

這樣，在平面內畫兩個方向不重疊、原點重合的數軸，組成坐標系，可以描述平面內的點的位置。如果方向垂直，那么形成的是直角坐標系;如果方向不垂直，形成的是傾斜坐標系。教師向學生介紹在數學史上傾斜坐標系是被笛卡爾和費馬發明出來，之后經過長時間的使用大家認為直角坐標系更為方便、實用，所以現在一般使用的是平面直角坐標系。

4.坐標系應用及發展

坐標系還有極坐標系、雙坐標系、三維空間坐標以及更高維空間坐標等，在高中會學習空間直角坐標系、平面極坐標系、柱坐標系和球坐標系。

教師講述關于三維空間坐標系笛卡爾與蜘蛛的典故。在教學中用數學家的故事增強教學趣味性，提升學生學習數學的興趣。

五、結論

如克萊因所說：學生現今在學習上遇到的困難，在歷史上也被數學家所遇到[10]。學生在課堂上了解數學家和數學史，經歷數學家探索數學知識的過程，能喚起他們對數學家的敬佩之情，激發他們對數學學習的好奇心及求知欲，幫助學生以更廣闊的視角來看數學，增加學生對數學及其社會文化背景的領悟。借助數學史實施教學，重構歷史，實現弗賴登塔爾倡導的“數學再創造”，能夠使教學更具趣味性，幫助學生愛上數學，也能使HPM擺脫“高評價、低應用”的尷尬境地。

參考文獻：

[1]蒲淑萍，汪曉勤.教材中的數學史：目標、內容、方式與質量標準研究[J].課程·教材·教法，2015，35（3）：53-57.

[2]彭剛，汪曉勤，程靖.數學史融入數學教學：意義與方式[J].成都師范學院學報，2016，32（1）：115-120.

[3]汪曉勤，王苗，鄒佳晨.HPM視角下的數學教學設計：以橢圓為例[J].數學教育學報，2011，20（5）：20-23.

[4]張俊忠，綦春霞.發生教學法：起源、理論基礎與應用：以數學教育為例[J].中學數學雜志，2015（2）：1-4.

[5]吳駿，汪曉勤.發生教學法：從理論到實踐：以數學教學為例[J].教育理論與實踐，2013，33（2）：3-5.

[6]Freudenthal H. Major Problems of Mathematics Education[J].Educational Studies in Mathematics，1981，12（2）：133-150.

[7]李文林.數學史概論[M].北京：高等教育出版社，2002-08.

[8]Kline M.古今數學思想[M].北京大學數學系數學史翻譯組，譯.上海：上?？茖W技術出版社，1979.

[9]岳秋，張德榮.“平面直角坐標系”：利用歷史故事，實現維度跨越[J].教育研究與評論（中學教育教學），2016（11）：32-37.

[10]王振輝，汪曉勤.數學史如何融入中學數學教材[J].數學通報，2003（9）：18-21.

作者簡介：許紫晨（1998—），女，北京人，太原師范學院碩士研究生。

郭劉龍（1964—），男，山西聞喜人，太原師范學院數學系副教授，主要從事數學教育研究。