基于核心素養的高考試題難度分析

劉浩 康寶林

摘 要：本文借助喻平的數學關鍵能力評價指標框架和鮑建生的綜合難度模型，分析高考試題中所蘊含的核心素養水平和試題的難度，以及它們之間的關系。最終得出高考試題的綜合素養水平和綜合難度之間有密切聯系，基于此，提出了幾點建議。

關鍵詞：數學核心素養;難度;高考試題

中圖分類號：G633 ?文獻標識碼：A ?文章編號：1673-260X（2021）07-0101-05

1 問題的提出

2014年3月，“核心素養”一詞被正式提出，引發了社會的高度關注。數學課程目標中，含有對數學學科核心素養的要求，一些數學試題設計的理念也包含數學核心素養，這就意味著在數學學習中教師要注意培養學生的核心素養。隨著核心素養的提出，試題的難度也在發生變化，并且核心素養的測評是以區分度為依據的，而區分度和難度之間又有重要聯系[1]。基于此，考慮核心素養和試題難度之間的關系。

本文以2020年高考全國卷Ⅰ理科數學試題為例，來探討高考試題中所蘊含的核心素養和其難度之間的聯系。

2 研究設計

2.1 數學核心素養的量化

2.1.1 數學關鍵能力評價指標框架

由于六大核心素養本身含義具有抽象性，很難對數學試題進行六大核心素養水平的劃分。于是，本文采用了喻平的數學關鍵能力評價指標[2]。他給出了六個核心素養三級水平的操作性定義，如表1所示。

2.1.2 綜合素養水平

為了更直觀地分析出每道題的綜合素養水平和難度之間的關系，需要對每道題的所蘊含的核心素養進行量化。每道試題所蘊含的核心素養經過量化之后稱為每道試題的綜合素養水平[3]。為了得到每道試題的綜合素養水平，首先，需要對表1中核心素養的每級水平進行賦值，在賦值時要考慮試題的區分度，還要體現每道題所蘊含的核心素養水平越高，其綜合素養水平也越高，因此，給表1中每個核心素養的一、二、三級水平分別賦予1、3、7的分值。然后，參考劉清等人的綜合素養水平計算公式，計算每道題的綜合素養水平，綜合素養水平計算公式定義為：。其中，d代表綜合素養水平，dij代表核心素養i的第j級水平的賦值，ni代表蘊含核心素養i的題目個數，n代表題目總個數[4]。比如，一道大題中含有三個小問，第一、二小問都處在邏輯推理和數學運算的第一級水平，第三小問處在數學抽象的第二級水平、邏輯推理的第二級水平，以及數學運算的第一級水平。根據上面計算公式，得到這道試題的綜合素養水平為：。

2.2 綜合難度模型

試題的綜合難度是指在正式測試之前由學科專家根據自身以往經驗對試題進行綜合評估得到的。

在量化試題的綜合難度時，為了較好地反映出數學試題的難度水平以及概括出學生數學完整的活動過程，本文采用鮑建生教授的綜合難度模型。此綜合難度模型包含五個難度因素，每個難度因素下面細分了多種水平[5]。該模型如表2所示。

模型計算公式di=nij=n，i=1，2，…），其中，di（i=1，2，3，4，5）表示5個不同的維度，nij表示題目中處在第i個維度中的第j個水平的題目的個數，dij為第i個維度中的第j個水平的權重（依水平分別取1，2，3，…），n代表題目總個數。根據模型計算公式可得出每道題在五個難度因素量化后的取值[5]。比如一道綜合題有兩問，第一問無背景，數學認知方面屬于理解層面，運算方面屬于簡單符號運算，推理方面是簡單推理，含有兩個知識點;第二問無背景，數學認知方面屬于應用，運算方面屬于簡單符號運算，推理是復雜推理，含有兩個知識點。則根據模型計算公式，這道題在五個難度因素上的取值依次為1，2.5，3，2.5，2。由此得出刻畫試題綜合難度的雷達圖。

3 數學試題綜合素養水平和綜合難度分析

2020年高考全國卷Ⅰ理科數學試題中設有選擇題、填空題、解答題，對答案中沒有詳細解答過程的題型，在水平劃分時，要避免一些解題技巧，采用一般的解法進行劃分[6]。全國卷Ⅰ中的第22、23題為選做題，本文對此不進行研究，排除這兩道題，對試卷中的其他題目，按照數學關鍵能力評價指標框架給出的操作性定義，對試題進行核心素養水平劃分。

3.1 高考試題綜合素養水平具體分析

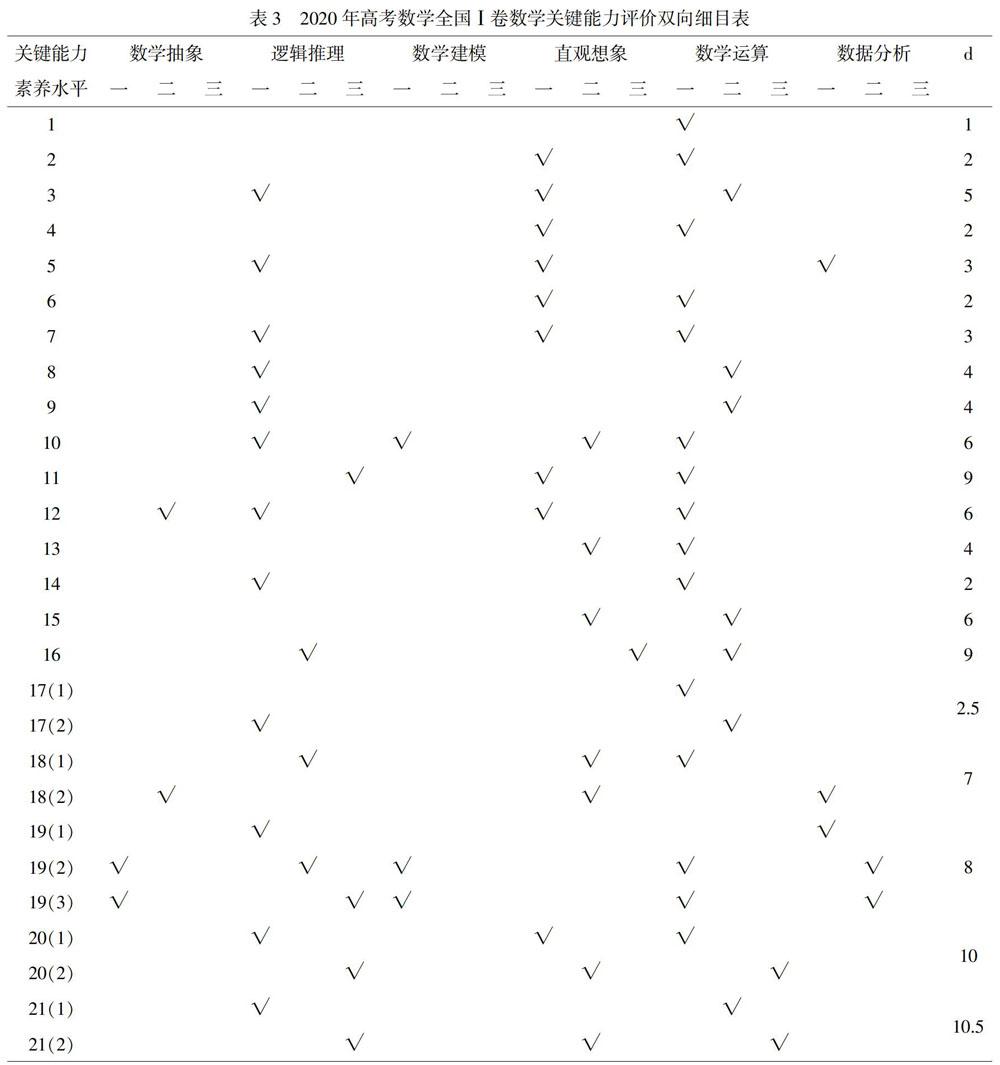
采用上文提到的核心素養量化方法，列出2020年高考全國卷Ⅰ理科數學試題關鍵能力雙向細目表，并根據綜合素養模型公式在表中列出每道題的綜合素養水平（用d表示），如表3所示。

2020年高考全國卷Ⅰ理科數學試題總題量為21道。有3道題里面含有數學抽象，并集中在一、二級水平，在第三級水平沒有分布;有15道題里面含有邏輯推理，在一、二、三級水平都有分布，主要集中在第一級水平，在第三級水平的題目分別是選擇題的11題，解答題的19、20、21題的最后一問;有2道題里面含有數學建模，且都處于第一級水平;有15道題里面含有直觀想象，在一、二、三級水平都有分布，主要集中在第一級水平，在第三級水平的題目填空題的第16題;有21道題里面含有數學運算，在第三級水平有20、21題的最后一問;有3道題里面含有數據分析，在第三級水平沒有分布。

從橫向觀察，選擇題第10題至第12題，填空題的第16題，以及解答題的18題至21題，“√”明顯增多，由此可以發現這幾個題所蘊含的數學核心素養的個數是比較多的，也就是綜合素養水平比較高。

表3的最后一列代表每道題的綜合素養水平，從數字看出，在選擇題、填空題、解答題三個題型的各個部分分值是遞增的。結合題目所處的位置，不難得出，高考壓軸題的綜合素養水平是比較高的。

總體來看，“√”大多分布在數學計算、邏輯推理和直觀想象部分，也就是幾乎每道高考題都蘊含著數學計算、直觀想象和邏輯推理的數學核心素養，正如羅素所說：“數學是符號加邏輯”，而在分析高考題的過程中也發現，大多數的題目意在考察學生的符號運算及證明，由此可以看出高考試題非常注重對這三種數學核心素養的考查。

3.2 高考試題綜合難度具體分析

采用鮑建生的綜合難度模型，列出2020年高考全國卷Ⅰ理科數學試題綜合難度雙向細目表，并在表中用各維度和的形式列出每道題的總難度系數（用f表示），如表4所示。

2020年高考全國卷Ⅰ理科數學試題總題量為21道。在“數學認知”維度，“識記”層面的有2道，“理解”層面的有7道，“應用”層面的有8道，“探究”層面的有4道，大部分題目集中在“探究”層面。考查學生在實踐的情境中轉化和應用知識的能力。

在“背景”維度，“無背景”層面的有18道，“個人生活”層面的有2個，“科學情境”層面的有1個，大部分題目沒有問題背景，直接考察學生對于知識點的掌握和運用情況。

在“運算”維度，“無運算”層面的有1道，“數值運算”層面的有2個，“簡單符號運算”層面有13個，“復雜符號運算”層面的有1個。題目大部分集中在“符號運算”層面。而且在分析試題中也發現，大多數的計算，更加偏重于符號的運算，單純考查學生純數值計算的題目很少。

在“推理”維度，“無推理”層面的有3個，“簡單推理”層面的有11個，“復雜推理”層面的有3個。大部分題目中含有簡單推理，也就是要求學生能夠在思考之后，選擇合適的知識和方法，進行作答。

在“知識含量”維度，“一個知識點”層面的有6個，“兩個知識點”層面的有7個，“多個知識點”層面的有6個。大部分題目都注重兩個或兩個以上知識點的考查，也就是考查多個知識點相互融合的題目。

從橫向觀察，可以看出本卷中有幾個難度系數較高的題目，分別是選擇題的第12、13題，填空題的16題，和解答題的20、21題。這些題都在各類題型的最后兩道，這與表3中綜合素養水平的呈現趨勢是一樣的。

3.3 2020年全國卷Ⅰ綜合素養水平和試題綜合難度對比分析

為了更加直觀地分析本卷綜合素養水平和綜合難度系數之間的關系，下面繪制關于綜合素養水平和綜合難度系數的折線圖。以題號作為橫坐標，以每道題的綜合素養水平和其對應的綜合難度系數作為縱坐標。

從圖2中可以看出，兩條曲線的走勢大致相同，兩者出現的峰值位置和低谷位置也大致相同，異常點僅出現在第5、13題，這說明一道題的綜合難度系數和它的綜合素養水平有很大關系。從圖中還可以發現，高峰值出現在選擇題的后兩道、填空題的后兩道以及解答題的后兩道，也就是我們所說的“壓軸題”的位置，由此說明高考題的設置遵循先易后難的順序，這有利于廣大考生合理的安排自己的做題時間和順序，合理的運用自己的答題策略，以便獲取更加理想的分數。

4 結論和建議

4.1 結論

通過本文分析，可以得出，在高考卷中，一道試題的綜合素養水平和綜合難度系數有密切聯系，即一道試題的綜合素養水平和綜合難度系數呈正比關系，兩者互相影響。并且，高考卷中的壓軸題一般都在各類題型（選擇題、填空題、解答題）的后兩道，壓軸題的綜合素養水平和難度系數都是最高的，這與我們傳統的想法相一致。

4.2 建議

4.2.1 設置試題“背景”

在分析試題難度時，“背景”這一維度引起了我們的關注，只有三個題設置了題目背景，即第3題以考生熟知的金字塔為背景設置問題，解答題第18題設置了圓錐背景，第19題以熟悉的羽毛球比賽為背景設置了相對容易的概率問題。其他試題沒有任何實際背景，單純考查高中一些主要知識點。

在高考命題時，除了一些“個人生活”“公共常識”，還可以多設置一些“科學情境”類的背景，但是，要注意在試題中不要盲目地加入背景，要注意加入的背景和題目的有機聯系，不要因為有背景的加入而使得問題空洞，讓學生產生厭煩的情緒。

4.2.2 均衡考查六大核心素養

在分析高考試題時，發現試題中仍然有一些不合理的地方。試題中蘊含關于數學運算、邏輯推理、數學建模、直觀想象的題目數量居多，而含有數據分析和數學抽象的題目卻很少，這樣的命題會使學生自身發展不均衡，不利于培養學生的綜合能力。

核心素養是學生經過知識的學習之后所能剩下來、帶得走、可再生的東西[9]。高考不應該只成為選拔人才的工具，還應有提高全民數學核心素養的目的。在命制試題時，注意相對均衡地考查學生的核心素養水平，切莫只關注分數的高低。

4.2.3 把控試卷難度

從試題分析可知，試卷整體難度比較大，要平衡試卷的整體難度，又不影響壓軸題的區分度，就要在試卷的其他試題下手，降低難度，可以通過改變其他試題的綜合素養水平，來達到降低難度的目的，主要的方法有：降低其他試題所考查的核心素養個數及核心素養水平的等級;提高壓軸題所考查的核心素養個數以及提高每個核心素養的等級水平。

4.2.4 完善核心素養的測評體系

本文在對試題所蘊含的數學核心素養進行量化時，采用的是喻平的數學關鍵能力評價框架，在此框架中對六個數學核心素養進行了知識理解、知識遷移、知識創新的三級水平劃分，這三個水平要求依次提高，由此發現框架本身可能受難度因素的些許影響。若要刨除這部分影響，進一步對結論進行驗證，還需對核心素養的測評體系進行完善，從而能更有效地使核心素養不斷融入高考試題。

參考文獻：

〔1〕雷新勇.大規模教育考試科學屬性之理論和實踐思考[J].教育與考試，2007，24（01）：31-37.

〔2〕喻平.數學核心素養評價的一個框架[J].數學教育學報，2017，26（02）：19-23+59.

〔3〕喻平.基于核心素養的高中數學課程目標與學業評價[J].課程·教材·教法，2018，38（01）：80-85.

〔4〕劉清，胡典順，張莘鈿.核心素養視角下的高考試題難度探析——以2019年高考數學全國卷（理科）為例[J].數學通報，2020，59（12）：34-40.

〔5〕鮑建生.中英兩國初中數學期望課程綜合難度的比較[J].全球教育展望，2002，31（09）：48-52.

〔6〕薛歡，杜劍南，路江江.2016—2020年高考數學（理科）全國卷“統計與概率”試題探析——基于綜合難度模型[J].教育測量與評價，2020，13（12）：30-40.