簡論高中數學練習教學的有效策略

米慧

【摘 要】高中數學難度較大且知識之間關聯性強，想要提升數學能力，學生就要進行大量練習。而受到各種因素的影響，一些高中開展的數學練習活動存在效率不高的問題。教師以及學生將大量的精力與時間浪費在無效練習上，不僅浪費教學資源，也會給高中生帶來很大的學習壓力。針對這一情況，數學教師需要對數學練習教學進行優化，以提升數學練習的有效性。

【關鍵詞】高中數學;練習教學;有效策略

【中圖分類號】G633.6? 【文獻標識碼】A? 【文章編號】1671-8437（2021）22-0029-02

與其他學科相比，數學的知識點具有一定的難度，想要更好地掌握數學知識，高中生不僅需要擁有良好的邏輯思維能力和空間想象能力，還要通過反復練習鞏固數學知識。傳統教學模式下，部分數學教師在開展數學練習活動時僅將課本中的例題及其簡單變形作為練習題，通過大量機械式訓練幫助學生鞏固數學知識。這種高強度的訓練會給高中生帶來巨大的心理壓力，且難以充分發揮數學練習的作用，會導致教學效率難以提升。要解決這一問題，高中數學教師需要全面分析數學練習過程中存在的問題，同時結合學生實際情況制定具有針對性的優化方案，提升數學練習效率，通過科學有效的數學練習培養學生的數學核心素養。

1? ?數學練習教學中存在的問題

1.1? 難以將知識融會貫通

在數學練習中，一些高中生難以將所學習的數學知識融會貫通，雖然能夠順利解決課本中的例題以及例題的簡單變形，但是對于復雜變形則無從下手。同時，學生往往能夠快速解決簡單的試題，但是對于具有一定難度的試題則束手無策。造成這一問題的原因在于學生沒有真正理解該知識點，無法有效遷移知識[1]。

1.2? 練習缺乏合理性

除了無法將數學知識融會貫通之外，數學練習活動缺乏合理性也是一個常見的問題。筆者觀察發現，一些高中在開展數學練習活動時，依然采用傳統的題海戰術，讓學生通過“刷題”的方式強行記住數學知識。這種記憶方法效率較低，而且容易產生記憶偏差，在進行綜合練習時，很多學生會由于記憶模糊而思維混亂。導致這種問題的主要原因是教師設計的數學練習活動缺乏層次性。教師僅針對單獨的知識點開展強化訓練，而不重視知識點之間的關聯，導致很多學生掌握了大量分散的數學知識點，但是無法在頭腦中對這些零散的知識點進行總結與概括，沒有搭建起完整的知識框架。學生盡管看上去已經記住了知識，但是卻無法靈活運用這些知識去解決數學難題。針對學生的這一問題，一些教師在理解上存在偏差，認為學生無法處理較為困難的數學試題是由于知識記憶不牢，因此在不改變傳統數學練習模式的基礎上提升練習強度，形成了惡性循環。

2? ?高中數學教學中開展練習教學的具體方式

2.1? 讓練習更具層次性

針對數學練習缺乏合理性的問題，教師要積極對數學練習模式進行優化，根據學生的數學基礎及學習習慣，靈活調整數學練習方式，讓數學練習更具層次性。具體而言，可以適當減少基礎題型以及書中例題的訓練量，為學生預留充足的課堂時間來練習變式問題，通過這種方式減輕學生的學習壓力。需要注意的是，一些學生的數學基礎較差，解決較為復雜的數學試題時較為吃力。因此，數學教師要對練習教學形式進行調整，以課本上的基礎題型為切入點，在提煉出相關知識之后，將其作為已知條件編入新的試題當中，借助這種方式，讓原本相對獨立的數學知識點能夠建立密切聯系。學生在進行數學練習時，會發現不同試題的已知條件以及求導結果可以相互轉化，就能將零散的數學知識點串聯在一起，讓數學練習活動發揮出真正的作用[2]。

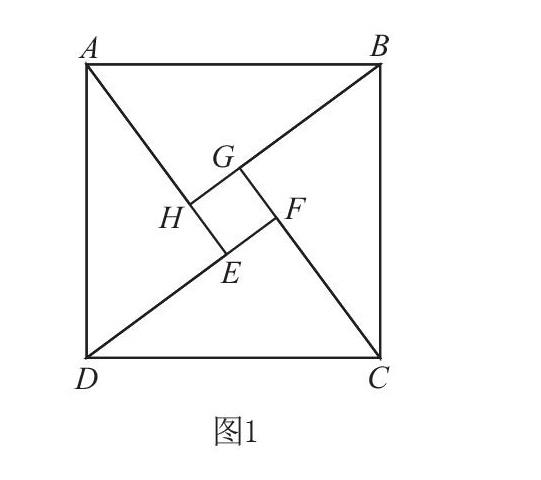
如在學習三角函數時，教師可先列舉下面這道試題：已知大正方形是由4個全等三角形以及一個正方形構成（如圖1所示），假設小正方形的面積為1，大正方形面積為25，設全等直角三角形中較小的銳角為θ，求cos2θ的值。這道題主要考查學生對三角函數基礎知識的掌握情況，直接計算cos2θ的值較為困難，因此需要借助三角函數基本定理求出sin2θ的值，通過這種方式反推cos2θ的值。先根據已知條件中兩個正方形的面積之比，分別求出兩個正方形的邊長。然后根據三角函數定義公式列出算式：5cos θ?5sin θ=1。之后再利用同角三角函數基本關系定理，計算得出sin2θ的值，進而得到cos2θ的值為。解決完這道題之后，教師可以將該題的答案轉變為另一道試題的已知條件，讓學生更為深入地掌握三角函數基本定理。

2.2? 靈活調整練習難度

針對部分學生無法靈活運用數學知識點解決數學試題的問題，教師要對數學練習的難度進行調整。目前一種有效的方式是采用漸進式習題練習模式。與傳統數學練習模式相比，這種模式具有較高的靈活性。在備課過程中，教師可以列出大量試題，然后再根據試題的難度將其分類。開展數學練習活動時，教師先讓學生解決簡單試題，并根據學生的練習反饋隨時調整難度。一旦發現大部分學生出現解題困難的情況，便不再繼續提高難度，而是帶領學生對此類問題進行逐步解析，弄清楚該題型的解題難點及解題方法。這種漸進式練習模式的一大優勢就是可以最大限度調動學生的練習積極性，數學基礎好的學生不會由于試題簡單而產生懈怠心理，數學基礎差的學生也不會因為訓練試題難度過高而放棄訓練，這樣能確保班級整體數學水平穩步提升[3]。

如在學習數列知識時，教師可以布置一道多問試題，先讓全部學生計算較為簡單的第一問，然后根據實際情況處理第二問。如果大部分學生能快速解決第一問，則可以讓學生獨立解決第二問，若大部分學生無法快速處理第一問，教師就要帶領學生一同分析第二問。

如這道例題：已知等比數列{an}的各項均為正數，且該數列滿足a3是3a1與2a2的等差中項這一條件，且a1a2=a3，①求{an}的通項公式。②假設bn=log3an，且Sn是數列{bn}的前n項和，計算數列的前n項和。第一問是求數列的通項公式，該問考查數列基礎知識，難度較低，教師可以讓學生獨立處理。第二問較為復雜，教師可以依據實際情況對該問進行解析，幫助學生更好地掌握數列知識。

2.3? 了解學生真實情況，提升練習有效性

除了要靈活調整訓練難度，以及讓數學訓練更具層次性之外，教師還要及時了解學生的真實學習情況，并根據學生數學練習的反饋，對數學練習模式以及練習內容進行調整。實際開展數學練習活動時，教師要讓學生詳細寫出解題步驟，通過分析學生所寫的解題步驟來了解學生的解題思路以及解題技巧，針對其中存在的問題，制定具有針對性的提高方案。教師可以布置一道具有一定難度的例題，讓學生通過自由討論或小組討論，探究解題思路、解題步驟等，分析各種不同解題思路之間的關聯。學生通過對解題步驟以及解題思路的討論，能夠充分展示自己的思維方式以及解題習慣，通過長期大量的觀察，數學教師可初步了解學生的數學思維模式。一旦發現某些學生陷入思維定勢，教師就要利用數學練習對其進行積極引導，幫助其盡早擺脫思維定勢的束縛。此外，教師在備課過程中還要積極利用互聯網，在網絡上搜集一些經典試題，同時學習新的教學理念以及解題技巧，以此來提升學生解題效率[4]。

數學科目作為高中階段的基礎學科之一，其重要性不言而喻。如何提升數學教學效率一直以來都是教師關注的焦點。想要提升數學教學效果，一個重要的途徑就是要提高數學練習效率。針對部分學生在數學練習活動中出現的問題，教師要給予充分重視，深入分析產生問題的原因。同時教師要結合學生實際情況，制定具有針對性的優化策略，確保數學練習教學發揮出應有效用，為提升學生數學綜合素養提供幫助。

【參考文獻】

[1]楊靜雅.高中數學解題過程中培養學生的反思能力的研究[J].中外企業家，2020（15）.

[2]黃永明.高中數學練習的分層實驗研究[D].重慶：西南大學，2020.

[3]朱海燕.巧用小組合作 優化高中數學教學[J].名師在線，2020（9）.

[4]趙琰.高中數學練習課的有效路徑[J].數學大世界（上旬），2019（10）.