核心素養背景下小學生運算能力的培養策略

彭國慶

[摘 要]運算能力是數學核心素養之一，在小學數學教學中可以運用“多元表征以明運算之理、多類型練習以熟運算之術、融入問題解決以善運算之用、多內容關聯以通運算之道”四個策略培養學生的運算能力。

[關鍵詞]運算能力;培養策略;核心素養

運算是小學數學教學中最傳統的內容之一，運算能力自然也備受重視，成為大家關注的基礎學習能力之一。《義務教育數學課程標準（2011年版）》將運算能力確定為十大數學核心概念之一，關于運算能力的描述是“運算能力主要是指能夠根據法則和運算律正確地進行運算的能力” 。下面筆者就結合自己的教學實踐從“明理、熟術、善用、通道”這四個方面談小學生運算能力的培養策略。

一、多元表征以明運算之理

數學學習不僅要關注學習的結果，更要關注學習的過程。教師在教學中經常遇到這樣的情況：學生在家長或非專業人員的提前教學下已經學習了兩位數乘兩位數的計算方法，但他們對算理卻理解甚少，如學生在計算36×12時，能夠記住36×12的豎式書寫程序，但是對于2乘36、1乘36的結果分別表示什么，乘積又表示什么，卻說不出來。對算法理解的多少不僅會對后續的運算學習有影響，還影響著問題解決的能力，所以計算教學不僅要教學生知道怎么算，還要結合具體內容采用多元表征方式幫助學生理解算理。

1.創設情境，理解算理

數學運算本身是抽象的，因此學生會感覺計算是枯燥的，理解算理更是猶如在枯燥的程序中尋找枯燥的理由。然而，合適的情境可以破除“枯燥”并幫助學生在有意義的、有趣的情境中理解算理。如計算36×12，教材呈現了這樣的數學情境圖（如圖1）：

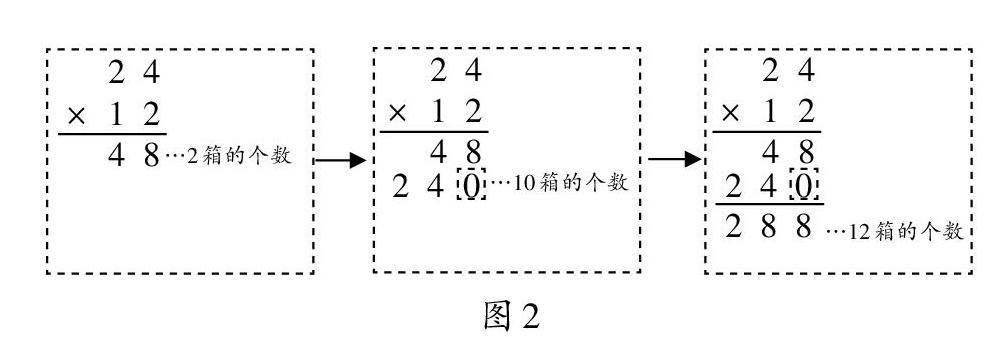
要計算12箱南瓜有多少個，可以分兩步：先算2箱有多少個南瓜，算式是2×24=48（個）;再算10箱有多少個，算式是10×24=240（個）;然后把兩次計算的總數相加，得到48+240=288（個）。這樣就是把12箱南瓜的個數進行分拆計算，而這樣的分拆計算，正好可以幫助學生理解24×12的豎式計算過程（如圖2）。

至此，教師再針對豎式中的每一步進行提問，幫助學生理解每一步運算的含義以及最后結果的含義，進而達到知其然知其所以然的學習目的。

再如，教學混合運算時，創設問題情境可以有效幫助學生理解混合運算的順序。如1副羽毛球拍是70元，1個羽毛球是4元，買2個羽毛球和1副羽毛球拍一共要多少元？要解決這個問題就要先算出2個羽毛球一共要多少元，算式是2×4，然后再加上1副羽毛球拍的錢數，寫成綜合算式是70+2×4。把分步計算的過程對應到遞等式過程中來，學生就能夠理解乘法和加法的混合運算中為什么要先算乘法了。

2.動手操作，理解算理

動手操作是學生學習數學的有效學習方式。在計算教學過程中，動手操作可以幫助學生把抽象的數理應用過程變為具象化的可視化操作活動，使學生在可視化的操作活動中充分理解算理，掌握算法。如教學用湊十法計算9加幾的加法計算時，教師先出示一個和例題同樣的情境圖，即“一個盒子里裝有9個蘋果，盒子外面有4個梨”（有經驗的教師都是用可移動的板貼圖來表示），然后提出問題“一共有多少個水果？”。學生可以將1個梨“放”進裝有蘋果的盒子里，湊滿10個，然后再加上盒子外面的3個梨，這樣得出一共有13個水果。最后讓學生完成“試一試”（如圖3）。

學生在移一移、圈一圈的操作活動中，理解了用湊十法計算9加幾的方法的分解過程，體會到湊十法計算的快捷性，還為后面繼續學習8、7、6等加幾做好了鋪墊。

3.幾何直觀，理解算理

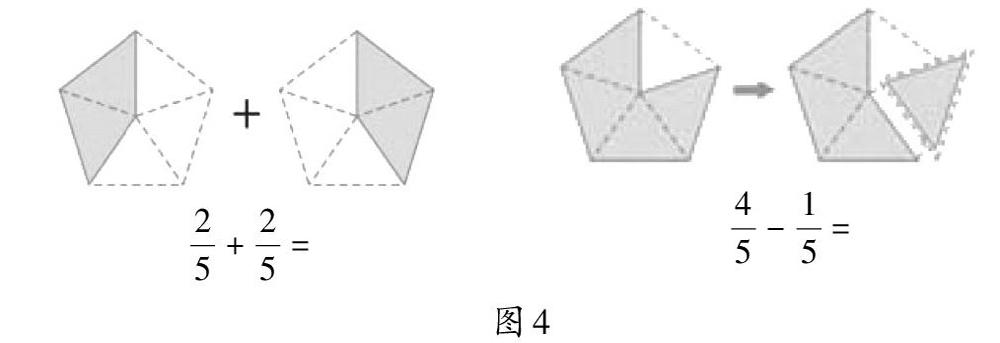
數是抽象的，形是具象的，在運算的過程中可以通過幾何直觀幫助學生理解算理。如對于同分數加減法，教材呈現了這樣的幾何直觀圖（如圖4）：

又如，在計算分數乘分數的時候，教材呈現了將長方形面積等分和再等分圖（如圖5）幫助學生理解分數乘分數的算理。

兩次等分圖既展現了計算的過程，同時又包含計算的結果，可以說是幾何直觀中的經典之作。通過這樣的直觀圖就能幫助學生理解分數乘分數就是分了再分、取了再取的道理。

二、多類型練習以熟運算之術

對學生運算能力的培養還需使學生能夠熟練應用運算方法進行快速、正確的運算，具體體現在加強對學生口算、估算、筆算（豎式計算、遞等式計算）能力的培養。

1.加強口算練習

口算是所有運算的基礎，加強口算練習，就相當于做好運算學習的塔基工程。口算練習要從一年級抓起，從10以內的加減法開始逐步拓展到多位數的口算，逐步加深口算的難度;從整數的口算到小數、分數、百分數的口算，從數的口算到式的口算，逐步拓展數與代數的運算領域，從而拓展口算練習的寬度和高度。 要加強口算練習就要天天練，練習的內容主要以與即將學習的新知有關的舊知（運算）以及學生易錯的口算題為主，每天練習的量為10題左右，保證學生能在加強基礎口算的同時，糾正一些常見的口算錯誤。口算的形式可以題組對比的方式，例如在兩位數乘兩位數的口算中設置對比題25×4和24×5，可幫助學生區分算式不同的同時培養學生認真審題的習慣。

2.加強估算練習

估算是學生進行運算以及檢驗運算結果的方式之一，但學生的估算正確率遠遠低于口算和筆算的正確率，一方面是估算的應用頻率較低，另一方面是學生的估算意識沒有初步形成。這樣就造成了學生在解決實際問題時估算能力不足，教師亟須把現實生活中應用廣泛的估算與數學中的估算學習對應起來。加強估算，首先要掌握估算的方法。在學生剛認數時，經常給出“17和12這兩個數，哪個數最接近20？哪個數最接近10？”這樣的練習，就是在為后面學生學習估算做好準備，而后讓學生在具體的問題情境中認識到估算的必要性，理解估算的方法。如創設問題情境：張大叔把收獲的生姜裝在同樣大的袋子里， 一共裝了 40袋， 他稱了其中的 4 袋， 結果分別是 18 千克、 21 千克、19 千克、 23 千克。 他一共收獲生姜大約多少千克？學生體會到這些數都是接近20的，雖然有的數是超過20的，有的數是不足20 的，但是只要接近20都可以將其看成20后進行估算。通過解決問題，學生就能掌握估算的方法，體會估算的實際應用價值。

3.加強筆算練習

小學的筆算主要有兩種形式，一是四則運算，主要是列豎式進行運算，二是四則混合運算，主要是采用遞等式的方式進行運算，前者是后者的基礎，后者是前者的延續和再使用。筆算練習應該從低年級的加、減法和乘、除法開始，首先夯實進位加法和退位減法的基礎;其次夯實連續進位和連續退位的減法的基礎，這些都是學生的易錯點;再次夯實兩位數乘一位數的乘法和除法運算的基礎，在夯實運算的過程中加強算法的指導，如在乘法中重點指導學生掌握進位書寫以及乘積加進位數的方法，除此之外，還要幫助學生區分兩位數乘兩位數的兩次乘積的乘法運算和最后的加法運算，減少學生混淆這兩種運算的問題。四則混合運算是學生進行數運算的終極目標，學生在計算時不僅要熟練解決運算順序的問題，同時還要保證每一步計算結果的正確性，因此，混合運算的練習要本著由易到難的原則，在激發學生獲得成功感的同時提高學生的運算能力。在筆算練習中還要加強簡算練習，因為除了按照一定的規則、順序進行運算，簡算能運用運算規律或性質使得原本復雜的運算變得簡單和快捷。因而，加強簡算練習，除了能提高學生的運算能力，還可以培養學生的觀察能力、辨析能力和靈活應用知識的能力，培養學生思維的靈活性和深刻性。

三、融入問題解決以善運算之用

當下的運算學習多是融合在問題解決中，通過運算解決一些實際問題，增強學生的運算能力，因此在解決問題中還要強化學生善于運用合理簡潔的運算途徑去解決實際問題的能力。

1.善于運用估算解決實際問題

學生在日常生活中常常要解決一些關于預算的問題，如購買高鐵票：商務座2114元/張，一等座1095元/張，二等座689元/張，只買一種票，買3張要準備多少元？這個問題可以用筆算解決，也可以用估算解決，但是把每種票價都多看一點，看成整千整百數后進行估算，就很容易得出預算結果，如商務座看成2200元/張，3張大約需要2200×3=6600（元）;一等座看成1100元/張，3張大約需要1100×3=3300（元）;二等座看成700元/張，3張大約需要700×3=2100（元）。這就體現了課程標準中指出的“用合理簡潔的運算途徑去解決實際問題”。除了數與代數領域，估算在統計與概率領域中的應用也是比較頻繁的，如根據折線統計圖中給出的數據預測即將出現的數據;圖形與幾何領域中結合方格圖估計一個不規則圖形的面積;根據一個圓柱形玻璃瓶中水的體積，估測和它同樣的2個瓶子中的水的體積;等等。在諸多的問題解決中體會估算在問題解決中的便捷性，能增強學生估算的應用意識和使用頻率。

2.善于運用簡便運算解決實際問題

數學本身就是追求簡潔的，教師在教學問題解決策略時要善于選擇并運用簡便運算體現數學的簡潔性，以增強學生的運算能力。如計算長方形的周長時選用“周長=（長+寬）×2”進行計算，計算長方體的表面積時選用“S=2（ab+ac+bc）”進行計算，就比較簡便。一個問題可以用加法或者乘法計算解決時優選乘法計算，同理，一個問題可以用減法或者除法計算解決時優選除法計算。如解決“張曉華和趙麗同時從同一地點出發，張曉華向東走，每分鐘走60米;趙麗向西走，每分鐘走55米。經過6分鐘他們相距多少米？”這樣的問題時，教師就要引導學生選用“（60+55）×6”進行列式計算，盡可能使得運算簡便。當然，這種簡便運算的選擇是在對比的前提下產生的，所以教師在教學過程中要注意結合實際問題引導學生進行比較，在多樣化算法的基礎上實現算法的優化。

四、多內容關聯以通運算之道

所謂運算之道就是運算中蘊含的基本規律、基本性質等。學生學習運算，不僅要知道現階段所學運算的方法和算理，還要能夠善于發現、總結運算中的規律，善于將現階段所學的運算知識融入整個運算知識體系中去，以通曉運算之道。

1.疏通聯系，理解運算原理的一致性

數的運算猶如一顆石子投入水中，激起的漣漪不斷由內向外暈開形成的同心圓，這些同心圓是以運算的基本規則為圓心，不同類型的數為半徑的。教師在帶領學生學習運算的時候，要不斷地幫助學生梳理、分析現有知識與已有知識之間的聯系，找到它們的共性之處，使學生形成完整的認知結構。如對于加、減法計算都是基于相同計數單位上的數才能夠相加、減這一知識點，教師要幫助學生梳理為什么要小數點對齊;在教學異分母分數加、減法的時候，教師要引導學生明白通分成同分母分數進行加減運算的道理，然后把整數、小數、分數的加減運算方法進行梳理和對比，幫助學生找到運算方法的一致性，形成完整認知結構。再如兩位數乘兩位數的筆算過程中蘊含了乘法的分配律，所以教學乘法分配律時，教師要引導學生回頭看兩位數乘兩位數的運算過程，合理解釋這一運算律在乘法豎式運算中的應用，促進學生理解豎式和遞等式運算的內在原理的一致性。

2.勾連關系，理解運算規律和方法的一致性

數學知識之間是有內在的規律和方法一致性的。如教學整數除法時，教師要引導學生發現除法的規律，如被除數一定，除數越大，商越小。在整數、小數、分數的學習中不斷推廣這些規律后，學生就能體會到運算規律的一致性。又如學習了除法、分數、比之間的關系后，學生在學習分數基本性質時，就可以結合商不變性質解釋分數的基本性質，在學習比的基本性質時，就可以結合分數基本性質解釋比的基本性質……這樣的互釋使看似不同性質的規律通過內在的聯系呈現了一致性。再如乘法和除法存在互逆關系，教學分數除法的時候，借助倒數把分數除法轉化為分數乘法，就能使學生體會到兩種算法之間的一致性。這樣勾連運算之間的關系，能有效地把運算知識串聯起來，幫助學生構建新知識網絡。

3.關聯遷移，理解運算蘊含數學思想方法的一致性

數學運算能力還是多因素融合的能力，包含理解、運用數學思想方法。如在歸納總結加法交換律時，要求學生根據問題情境寫出幾個等式，經過觀察后發現規律，將這種合情推理的方法遷移到后續的加法和乘法運算律的學習中，所以在這些規律的總結方面要能夠體現數學思想方法的一致性。又如探究小數加法的計算方法時，借助人民幣單位把小數轉化成整數再計算，這種計算方法也能遷移到小數乘法、小數除法中。因此，在總結方法的時候，要關聯之前的運算方法，讓學生體會到這些運算方法中所蘊含的數學思想是一致的。

綜上，學生運算能力的培養是一項長期的工程，教師在平時的教學中只有持之以恒地去做，才能收到理想的效果。

（責編 金 鈴）