基于數(shù)學(xué)建模素養(yǎng)下概率模型的教學(xué)設(shè)計(jì)探究
汪菊玲 石育雄 安永軍

摘要:數(shù)學(xué)建模是對現(xiàn)實(shí)問題進(jìn)行數(shù)學(xué)抽象,用數(shù)學(xué)語言發(fā)現(xiàn)問題、用數(shù)學(xué)方法構(gòu)建模型解決問題的素養(yǎng)。本文以《幾何概型的應(yīng)用》教學(xué)為例,從教學(xué)設(shè)計(jì)的角度,精心設(shè)計(jì)其建模過程,不僅能夠讓學(xué)生掌握數(shù)學(xué)建模的方法,提高學(xué)生解決實(shí)際問題的能力,還能夠促進(jìn)學(xué)生數(shù)學(xué)核心素養(yǎng)的養(yǎng)成。
關(guān)鍵詞:數(shù)學(xué)建模;教學(xué)設(shè)計(jì);幾何概型的應(yīng)用
中圖分類號:A 文獻(xiàn)標(biāo)識(shí)碼:A 文章編號:(2021)-32-457
數(shù)學(xué)建模是通過對實(shí)際教學(xué)問題的簡化和抽象后,用數(shù)學(xué)原理建立模型,再解決相關(guān)的問題。在高中數(shù)學(xué)教學(xué)設(shè)計(jì)中,教師想要滲透數(shù)學(xué)建模素養(yǎng),應(yīng)將其融入在教學(xué)目標(biāo)、教學(xué)重難點(diǎn)、教學(xué)過程、教學(xué)總結(jié)等各個(gè)環(huán)節(jié),從而使學(xué)生能夠針對數(shù)學(xué)問題開展猜想與交流,實(shí)施探究活動(dòng),建立數(shù)學(xué)模型,解決實(shí)際問題。幾何概型作為新課標(biāo)新增加的知識(shí)點(diǎn),與生活實(shí)際緊密相關(guān),同時(shí)與幾何論證、計(jì)算等方面也有關(guān)聯(lián),因此在高考中出現(xiàn)的可能性較大,作為教師應(yīng)該有效設(shè)計(jì)教案,幫助學(xué)生掌握相關(guān)知識(shí)與技能。
一、問題引求知
教學(xué)目標(biāo)是一切活動(dòng)設(shè)計(jì)的中心點(diǎn)與落腳點(diǎn)。因此教師應(yīng)在教學(xué)目標(biāo)中體現(xiàn)出建模素養(yǎng),如將實(shí)際問題轉(zhuǎn)變?yōu)閿?shù)學(xué)問題,使學(xué)生通過猜想、探究掌握幾何概型的應(yīng)用能力等。幾何概型主要是用來計(jì)算基本事件可“連續(xù)”發(fā)生的有關(guān)概率問題,大多數(shù)是實(shí)際生產(chǎn)、生活問題。因此教師在教學(xué)設(shè)計(jì)過程中,可以采用生活類的問題,激發(fā)學(xué)生的求知欲望。既能夠滿足教學(xué)目標(biāo)要求,也能夠激發(fā)學(xué)生的探索欲望。例如,公交車是高中生經(jīng)常接觸的交通工具,為此教師便可以為學(xué)生創(chuàng)設(shè)一個(gè)生活問題情境,公交車站每隔15分鐘便會(huì)有一輛公交車到達(dá),但是我們到公交車站的時(shí)間是任意的,求你到達(dá)車站候車時(shí)間大于10分鐘的概率。
二、猜想引交流
當(dāng)問題提出之后,教師一定要給予學(xué)生時(shí)間進(jìn)行有效的猜想與交流,從而使學(xué)生打開探究思路,更好地解決數(shù)學(xué)問題。因此數(shù)學(xué)教師需要在教學(xué)設(shè)計(jì)中預(yù)留時(shí)間空間,讓學(xué)生發(fā)揮主動(dòng)性。為了將建模素養(yǎng)更好地落實(shí),此時(shí)教師便需要引導(dǎo)學(xué)生在猜想與交流中,將實(shí)際的生活問題轉(zhuǎn)變?yōu)榫唧w的數(shù)學(xué)問題。
首先,該問題是與長度有關(guān)的幾何概型問題,那么學(xué)生在猜想時(shí),首先要找到幾何區(qū)域D,緊接著找到事件發(fā)生在區(qū)域D對應(yīng)的區(qū)間d,在此過程中,學(xué)生需要找到一個(gè)關(guān)鍵點(diǎn),即確定邊界點(diǎn),但是邊界點(diǎn)是否取到并不會(huì)對事件的概率產(chǎn)生影響。
三、探究引思考
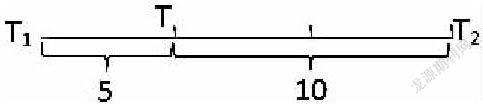
學(xué)生對該題進(jìn)行分析,將時(shí)刻抽象為點(diǎn),時(shí)間為線段,利用幾何概型的相關(guān)知識(shí)進(jìn)行解答。首先設(shè)前一輛公交車達(dá)到的時(shí)刻是T1,下一輛公交車到達(dá)的時(shí)刻是T2,此時(shí)根據(jù)題意,我們可以知道T1T2的長度為15,假設(shè)T是線段T1T2下標(biāo)上的某個(gè)點(diǎn),T1T的長度是5,TT2的長度是10(如圖)。
當(dāng)圖形繪制之后,教師再讓學(xué)生進(jìn)行自主思考與探究,也可以與同桌進(jìn)行相互交流,以此保證學(xué)生的“用腦”頻率,使學(xué)生始終處于思考狀態(tài)。思考過后,教師可以讓學(xué)生進(jìn)行自主分享,提出自己的探索經(jīng)過。
學(xué)生1說:“當(dāng)我去坐車的時(shí)候,將等車時(shí)間大于10分鐘當(dāng)作事件1,如果我到達(dá)車站的時(shí)刻t落在線段T1T之間,事件1發(fā)生。因?yàn)閰^(qū)域D的總長度是15,那么我等待事件超過10分鐘的區(qū)間d的長度是5,即:P1=d的長度D的長度=515=13,所以可以得出我等車時(shí)間超過10分鐘的概率是三分之一。
四、訓(xùn)練引鞏固
為了切實(shí)加強(qiáng)學(xué)生的建模素養(yǎng),教師可以在該題的基礎(chǔ)上進(jìn)行延伸與演變,使學(xué)生進(jìn)一步探索更多的數(shù)學(xué)奧秘,并鞏固目前學(xué)到的知識(shí)。如公交車每隔15分鐘到達(dá)一輛,每輛車會(huì)在站牌處停留3分鐘,此時(shí)再求等車時(shí)間大于10分鐘的概率。
該題在前一題的基礎(chǔ)上增加了難度,學(xué)生需要在之前的數(shù)學(xué)模型上進(jìn)行調(diào)整才能解決該問題。此時(shí)教師可以給學(xué)生一點(diǎn)提示,如教師為學(xué)生繪制一個(gè)圖形。
當(dāng)圖形繪制完畢之后,很多學(xué)生便有思路,繼續(xù)按照該模型進(jìn)行求解,此時(shí)設(shè)等車時(shí)間大于10分鐘的事件為A,此時(shí)我們到站時(shí)刻t便會(huì)落在T1T,所以就是P1=T1TT2T2=215
五、總結(jié)引完善
在課堂的結(jié)尾處,為了驗(yàn)證模型是否符合實(shí)際生活中的問題,教師可以帶領(lǐng)學(xué)生進(jìn)行結(jié)果驗(yàn)證,此時(shí)也可以向?qū)W生列舉更多相關(guān)的生活問題進(jìn)行解釋,使學(xué)生進(jìn)一步理解幾何概型的模型。最后,教師讓學(xué)生總結(jié)出幾何概型的數(shù)學(xué)模型,即先確定區(qū)域D,再確定事件落在區(qū)域D中相對應(yīng)的區(qū)間d,最后求出概率。
高中數(shù)學(xué)建模思想的培養(yǎng)和數(shù)學(xué)建模的應(yīng)用是數(shù)學(xué)教育的重要內(nèi)容,教師在教學(xué)中應(yīng)重視學(xué)生的建模思想和建模素養(yǎng)的培養(yǎng),加強(qiáng)學(xué)生建模意識(shí),提高學(xué)生課堂建模方法的能力,并鼓勵(lì)學(xué)生通過觀察、思考和論證等方法建立模型。同時(shí),數(shù)學(xué)學(xué)習(xí)作為一個(gè)與生活息息相關(guān)的話題,離不開既定的生活環(huán)境,教師的目標(biāo)是提高學(xué)生解決實(shí)際問題的能力,使學(xué)生善于觀察和總結(jié)數(shù)學(xué)生活的規(guī)律,強(qiáng)化建模思維在生活中的應(yīng)用,促進(jìn)學(xué)生數(shù)學(xué)綜合素養(yǎng)的全面提升。
參考文獻(xiàn)
[1]張應(yīng).在實(shí)際問題情境中體驗(yàn)數(shù)學(xué)建模——問題情境驅(qū)動(dòng)下的高中數(shù)學(xué)建模教學(xué)探討[J].數(shù)學(xué)學(xué)習(xí)與研究,2021(19):14-15.
[2]陳龍珠.高中數(shù)學(xué)建模的教學(xué)探究——以概率與統(tǒng)計(jì)教學(xué)內(nèi)容為例[J].福建教育學(xué)院學(xué)報(bào),2021,22(06):22-24.

