由一道題引發思考學生數據統計能力的培養

楊瑞芳

[摘 要]《統計與概率》這部分內容的學習，能使學生學會如何整理、分析和處理數據，會根據數據的特征和發展趨勢做出判斷與決策，可以有效促進學生形成正確的統計觀念，培養和提高學生的數據統計能力。

[關鍵詞]數據統計能力;培養;思考

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）33-0042-02

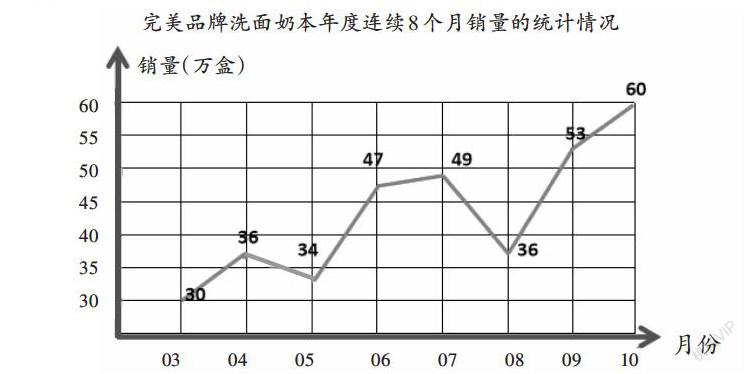
教學蘇教版小學數學《單式折線統計圖》后，教材中有這樣一道習題：“下面是一款洗面奶本年度連續8個月銷量的統計情況。問題：（1）分析統計圖中的數據可知，（? ）月的銷量最高，（? ）月的銷量最低。（2）仔細分析統計圖，你還獲知了哪些信息？（3）如果你是銷售總監，哪個月應多向經銷商供貨，為什么？”

對于問題（1），學生的解答很少出錯，而對于問題（2）和問題（3），學生的答案可謂千奇百怪。

一、追蹤成因

對于問題（2），只要是學生發現的信息，教師都可以給予表揚評價，因為這道題本身就是開放題，學生的關注點不同，答案自然不同。梳理學生的觀察角度，大致可分為三類，即“只關注局部的具體信息”“關注局部數據的增減變化”“關注整體數據的變化趨勢”，其中“只關注局部的具體信息”的學生占比59.3%。經訪談得知，許多學生忽視了數據比較和數據的整體變化趨勢兩個方面。《統計與概率》這部分內容每學期教材都有安排，從表格整理到條形統計圖，再到折線統計圖、扇形統計圖，經過長時間的學習，為什么還有那么多的學生沒有整體思考的意識？為什么學生還是只糾結于局部的詳細信息？我們不妨換位思考。

學生間客觀存在個體差異，分析統計數據時主要分為三個層次：低層次學生，只能發現直觀顯示的圖像信息;中間層學生，能對隱藏的信息進行邏輯推理，得出可靠的結論和規律，并能對數據的發展趨勢進行合理預判;高層次學生，能對數據的整體情況以及影響數據變化的因素進行合理推測，并能對事情的發展做出決策和規劃。

分析學生對于問題（3）的解答情況可知，其中大部分學生的判斷沒有足夠的依據，且由于數據較多，導致顧此失彼，難以考慮周全;有些學生則對某些節點或者線段的關注，遠遠超過對整條折線的關注;還有近四成的學生對“銷量”一詞不理解。

學生解決問題的方法與技巧不是一朝一夕就能形成的，需要經過長期的訓練與積累。調研時，學生的另一個缺陷也隨之暴露，即過于依賴已有經驗。在《統計與概率》教學中，學生解答錯誤并非完全歸咎于個體經驗的差異，實則教師對學生已有知識經驗的掌握和運用做得不到位，很多問題是教學不當所致。那么，教師該如何改進課堂教學呢？

二、解決策略

1.定量分析與定性分析的綜合運用

定量分析，指學生對折線統計圖中各個節點與線段所代表的意義的理解和把握，包括數據的大小、位置、與前后數據的對比以及處于上漲還是下滑趨勢、處于峰值還是谷底等。定性分析，指對折線的傾斜度、拐點、整體走勢、最值分析、波動頻率等的大致感受。當學生具備定量分析的能力后，教師可以引導他們向定性分析轉型升級，及時指導學生通過對各個數據的精準分析以及對整體情況的準確把握，做出合乎邏輯的定性分析。需要注意的是，學生初學習《統計與概率》這一內容時喜歡憑直覺推斷，這與定性分析的區別很大，因為前者是憑空臆想，后者則是建立在大量精確的數據分析之上，具有邏輯推理的成分。因此，定量分析與定性分析是辯證統一的關系。

案例：

（1）出示南京市某日氣溫統計表。

師：你能讀懂這個統計表嗎？（生答略）

師：（小結）如何將數據變得更加直觀易懂？

生：繪制相應的統計圖。

（2）出示折線統計圖。

①這是什么類型的統計圖？你以前見過嗎？（揭示：折線統計圖）

②你想了解這種統計圖的什么性質？（如折線統計圖的名稱從何而來，如何繪制，與其他統計圖相比有什么區別等）

（3）對折線統計圖建立感知。

①關注線段（隱藏各個數據）。

師：僅憑折線，你能讀取哪些信息？你的判斷依據是什么？（折線的傾斜度反映溫度的變化趨勢，即折線上升代表溫度升高，折線下降代表溫度降低）哪個時段的氣溫上升？哪個時段的氣溫下降？

②關注節點（局部突出）。

師：除了折線的傾斜度變化能夠反映氣溫的升降外，還有什么地方可以體現？這些節點分別表示什么？

③深入探究。

師：你還能獲知哪個轉折點的意義？

……

點和線是折線統計圖的基本結構。上述教學從氣溫入手，一條折線很直觀地展現出溫度變化的全過程，使學生分析時有理有據。同時，這一折線統計圖便于學生從整體上把握信息，因為折線統計圖本身就可以反映出數據的增減變化，各個數據呈現一個動態連續的變化過程，而條形統計圖的各個數據是割裂開來、孤立存在的，有利于將定量分析和定性分析合二為一，幫助學生對統計數據建立直觀的認識。在教學過程中，教師可通過問題引導學生進一步研究數據的增減變化情況，對點位高低、峰值與谷值的落差、線段傾斜度等隱性特征進行分析，深化學生對線和點的認識，學會如何利用這些隱性特征做出預判，使學生分析數據時的思維更加縝密和理性。

2.整體趨勢與關鍵信息兼顧

教師應該有這樣的覺悟：大數據時代，就是從海量的相關信息中總結出規律，使這些規律能夠成為對未來發展預判的依據，其中每一個看似孤立的、偶然的數據都與其他數據有著千絲萬縷的聯系，所以每個數據都很重要。這就是統計學中的隨機性，它在某種程度上或者在某個時間節點上起著影響未來走勢的作用。同時，教師應該讓學生明確，個別數據雖然偏離預期值，但這是偶發現象，是小概率事件，不會影響對整體發展變化趨勢的判斷。這是對學生已有知識經驗的一次補充和完善，使學生理性、全面地看待數據分析的結果。

案例：

清華大學熱能工程系

師：（小結）原來，橫軸上的數據代表的是屆別（年份），是按順序編排的，所以我們也應按順序連線。

（2）科學預判，感悟數據的隨機性。

①通過這幅統計圖，你能獲知哪些有用信息？

②哪兩屆碩士畢業生赴美留學人數的增長最快？你是怎么看出來的？

③請你預測一下清華大學熱能工程系2020屆碩士畢業生赴美留學的人數有多少？

師：（出示2020屆碩士畢業生赴美留學人數為32人）猜測一下，這是不是受到美國疫情和總統選舉的影響？

……

上述教學，根據折線統計圖，不僅可以獲知清華大學熱能工程系碩士畢業生赴美留學人數的變化趨勢，還能做出一定的預測，但是預測的結果無法保證百分之百應驗，因為這只是一個大概率的可能事件。接著，教師讓學生猜測清華大學熱能工程系2020屆碩士畢業生赴美留學的人數，然后出示真實的官方數據，使學生切身體會到數據變化的隨機性。學生對數據的猜想先是隨意，然后進行邏輯分析，最后基于邏輯之上正視隨機性的存在，這樣猜測會更理性。

總之，數學教學中，教師應注重培養學生的數據分析觀念，使學生的數據分析能力不斷得到提升，有效促進學生讀圖能力和統計分析能力的發展。

（責編 杜 華）