“啟發式”教學模式下的高中數學教學案例分析


摘要:在素質教育背景下,有大量教育學者倡導使用“啟發式”教學模式。該模式使用的教學內容和教學結構具有較強的啟發意義,整個教學過程科學合理,形成一個有機整體。在數學教學實踐中科學運用該模式,有利于促進學生思維能力的全面提升。
關鍵詞:高中數學;新課程;教學設計
新課程標準明確指出,學生自主學習能力非常重要,要求教師積極轉變教學觀念,摒棄傳統、落后的“灌輸式”教學模式,讓學生有更多的課堂參與感。許多學者也深入研究了新的課程標準,在此基礎上提出了大量的具有創新性的教學設計方案,但是很少有關于實際課堂教學的研究。基于這一研究現狀,文章重點探討了高中數學教學設計和教學過程,要求教師積極創設教學情境,鼓勵學生小組合作交流,并以高中數學必修5“正弦定理”為案例,給出了具體的教學設計方案。
一、 高中數學教學現狀
“正弦定理”較為復雜,知識點較為重要,因此該章節共計安排兩個教學課時。第一課時主要帶領高一學生重新回顧之前所學的三角函數基礎知識點,利用各類習題,加強學生對這些知識點的應用。本堂課的主要教學目標是引入“正弦定理”,并通過定理證明加強學生的記憶力。“正弦定理”既涉及舊知識點,也對后面的數學學習有非常重要的作用。學生應該利用“正弦定理”的學習培養自己的數學應用能力,主動在現實生活中靈活使用數學知識解決問題,嘗試自主建立系統、全面的高中數學知識結構框架。
二、 教學過程
(一)創設情境,引出例題
應用幻燈片展示課件,引出下列數學問題。
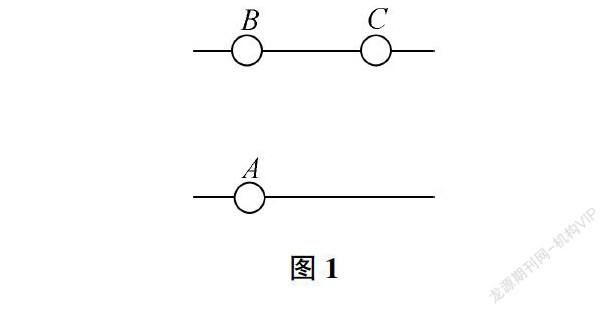
【例題】有一條寬為1km的河流,兩岸平行,近期,由于天氣惡劣,上游突發特大洪水,但碼頭A囤積了重要物資,還有若干名留守人員。為避免造成更大的經濟損失和人員傷亡,要抓緊時間利用船把碼頭A的物資和人員轉運到碼頭B或下游1km的碼頭C處。請按照要求制定合理的轉運方案,具體如圖1所示。已知條件:在靜水中,船速為v1=5km/h,水流速度v2=3km/h。
設計意圖:主要是考慮到該問題的背景與現實生活息息相關,符合高中數學中“數學源于生活”的教學理念,能夠幫助差生建立數學學習自信心,拉近了數學和學生之間的距離。同時,該情景問題的解題思路與“正弦定理”密切相關,奠定了良好的定理學習基礎。
師:請同學們利用已學的數學知識,聯系問題背景,思考如何制定最合理、成本最低的轉運方案。(學生分組討論)
討論環節結束后,教師結合教學目標,有針對性地篩選各小組討論的問題,最終總結為以下五個。
第一,船的終點應該是B處,還是C處?
第二,船開往B和C的行駛時間分別是多少?
第三,船開往B和C的行駛速度分別是多少?
第四,船從A到B和從A到C的行駛距離分別是多少?
第五,為了確保船能夠沿直線到達B,C,船應該往哪個方向開?
設計意圖:小組討論學習很好地克服了傳統教學模式的教學弊端,提高了學生的課堂參與度,學生相互交流,分別提出自己對問題的看法。當學生討論陷入困境時,教師作出適當的指示,討論結束后,再篩選問題,瞄準問題研究方向,提高教學效率。
師:請大家思考如何高效解決上述五個數學問題,并闡述這些問題的數學實質。(學生分組討論)
此時學生的討論熱情較為高昂,教師應深入課堂,和班級學生一同分析問題,嘗試從學生的角度引出問題:在三角形中,已知兩邊和其中一邊的對角,求另外的對角和第三邊。
設計意圖:把實際問題靈活轉化為數學問題,讓學生自主分析并解決問題,逐步形成問題轉化思維,通過建立模型把復雜問題簡單化。
(二)探尋特例,提出猜想
回顧直角三角形中的邊角關系:
sinA=a/c,sinB=b/c,sinC=1=c/c
師生活動:與班級學生交流,引導他們發現并總結規律,更加深入地理解直角三角形中的邊角關系,把握問題本質。在直角三角形中,c邊相同,利用這一特點進一步統一形式,最后發現,在直角三角形中a/sinA=b/sinB=c/sinC。
師:這個結論是否應用于任意三角形呢?(學生思考交流)
有的學生開始皺眉,陷入深思,教師可以先拋出一個個例驗證,把兩個全等的30°,60°的直角三角形拼在一起,驗證該定理(如圖2)。
提出猜想:有學生舉手,認為無論三角形是什么形狀,該結論都適用。
設計意圖:教師先利用直角三角形這一特殊三角形為教學切入點,再由特殊到一般,最后總結出具有普適性的“正弦定理”。類似的啟發式教學模式符合學生的認知規律。
(三)歸納推理,證明猜想
互聯網信息技術的應用豐富了課堂,提高教學效率。在猜想驗證環節,教師統一在多媒體上播放課件,由教師演示,學生仔細觀察并加以思考。教師在課件上任意改變三角形的形狀,計算機自動計算三角形各邊與角正弦值的比。
設計意圖:多媒體信息技術客觀驗證“正弦定理”,鞏固學生對該定理的認識。
師:以上考察都相當直觀,學生能夠從情感上接受該定理,但高中數學講究邏輯思維嚴謹,必須使用嚴格的數學推理證明“正弦定理”。那么,如果是銳角三角形,怎樣通過構造直角三角形,依次表示a和sinA,b和sinB的關系呢?
探究1是否能通過構造直角三角形,把問題由未知化為已知?
此時,學生議論紛紛,給出不一樣的作答:
生1:如圖3所示,過C點向BC作垂線CD,交BA延長線于D,得直角三角形DBC;
生2:如圖4所示,過A點向BC作垂線AD,把銳角三角形轉化為兩個直角三角形;
生3:如圖5所示,分別過B點和C點向AB和AC作垂線,交點為D,再連接AD,得兩直角三角形……
進一步討論后發現,方法1并不合理,予以排除,方法2較為簡潔,借鑒價值較大,容易得出b和sinB,c和sinC的關系式。而方法3延伸了問題,四點共圓,繼續利用圓的知識點可得:a/sinA=b/sinB=c/sinC=2R,這一解題思路同樣適用于鈍角三角形。
探究2是否可以引入向量,把“正弦定理”證明轉化為向量運算?
設計意圖:尋求正弦定理證明方法,讓學生舉一反三,深入體會各類數學思想。高中數學知識點較為零散,內容較多,學生平時學習時要特別注意知識點之間的內在聯系,遇到不會的問題可以考慮使用向量方法。
(四)定理形成,概念深化
“正弦定理”:在三角形中,個邊的長和它所對角的正弦的比相等。即,asinA=bsinB=csinC。
師:從結構來看,“正弦定理”的特征是什么樣的?有哪些變式?
1. 在結構上,各邊與其對角的正弦嚴格對應成正比例,非常和諧統一;
2. 從方程來看,每個方程都含有四個量,已知三個,求一個,這也正是“正弦定理”的用途;
3. 已知三角形的任意兩角及其一邊,可求其他邊;
4. 已知三角形的任意兩邊和其中一邊的對角,可以求其他角的正弦值,例如,sinA=absinB。
(五)范例教學,舉一反三
例1已知△ABC中,a=20,A=30°,C=45°,解三角形。
變式1若△ABC中,AC=3,A=45°,C=75°,則BC=______。
師生活動:教師先規范展示例1的解題步驟,直接使用“正弦定理”得出答案,變式1則布置為學生作業,獨立自主完成,教師統一批閱。
設計意圖:讓學生在具體問題中應用“正弦定理”,快速解決各類三角形問題。
(六)歸納小結,鞏固新知
師:本節學習內容結束了,你有哪些學習收獲?(師生共同總結,共同進步)
1. 掌握了“正弦定理”,能在三角形邊角關系問題中靈活使用“正弦定理”,提高解題速度;
2. “正弦定理”的證明方法;
3. 了解現實生活中,三角度量的簡單方法。
設計意圖:引導學生思維發散,完善現有的知識結構體系,總結學習心得。
(七)課后作業
1. 書面作業:習題1.11,2
2. 探究作業:
(1)在鈍角三角形中,探究用不同方式方法證明定理;
(2)已知三角形的兩邊和一角,這個三角形具備唯一性嗎?
教師要深刻意識到啟發式教學模式的教學意義,讓學生主導課堂,逐步引導學生找到問題答案,培養學生的創新意識。
參考文獻:
[1]張浩.基于探究的高中數學習題教學設計與實踐[D].貴陽:貴州師范大學,2014.
[2]任志鴻.志鴻優化系列叢書——高中優秀教案數學·必修5[M].海口:南方出版社,2010.
[3]吳建榮.高中數學中存在的問題及改進策略[J].西部素質教育,2017.
作者簡介:
張曉亮,甘肅省定西市,甘肅省通渭縣第一中學。

