基于學生立場的數學教材橫向比較與教學建議
劉兆偉


摘 要 基于學生立場,從情境創設、活動設計、文化滲透這三個方面,對人教版、蘇教版、北師大版和青島版教材中“三角形的面積”內容進行橫向比較分析,進而提出教學建議:情境創設從單元整體出發、活動設計從已有經驗出發、文化滲透從意義理解出發。
關鍵詞 學生立場 教材橫向比較 三角形的面積 情境創設 活動設計 文化滲透
《義務教育數學課程標準(2011年版)》(以下簡稱《課標》)指出:“數學教材為學生的數學學習活動提供了學習主題、基本線索和知識結構,是實現課程目標、實施數學教學的重要資源。”雖然不同版本教材的設計理念、編排體系與邏輯結構等不完全一樣,但它們都是依據《課標》編成的,教師在設計教學時,可通過對不同版本教材中的同一內容進行橫向比較分析,豐富對所教內容的認識和理解,從而設計出更有利于學生發展的學習活動。本文以“三角形的面積”一課為例,對人教版、蘇教版、北師大版和青島版教材進行橫向比較分析,并在分析的基礎上提出教學建議。
一、教材分析
1.對情境創設的對比分析
《課標》指出:“教材所選用的學習素材應盡量與學生的生活現實、數學現實、其他學科現實相聯系,應有利于加深學生對所要學習內容的數學理解。”人教版、北師大版和青島版教材都選用生活素材創設現實情境,以引發學生的學習興趣。人教版教材以紅領巾為學習素材,并直接提出問題:“怎樣算出紅領巾的面積呢?”北師大版教材以流動紅旗為學習素材,并直接提出問題:“如何求出這面彩旗的面積?”青島版教材中則以道路標志牌為學習素材,并用“你能提出什么問題?”引導學生提出問題:“制作這個標志牌需要多少平方分米的鋁皮?”
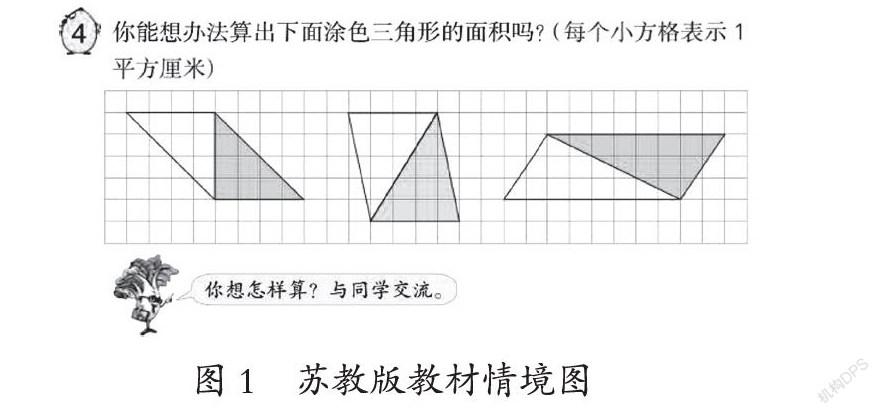
與上述三種版本教材不同的是,蘇教版教材選擇數學素材創設了純數學情境:將三種不同類型的三角形置于方格圖上的平行四邊形中,讓學生“想辦法算出下面涂色三角形的面積”(如圖1)。純數學情境注重的是數學知識間的內在聯系,學生在這樣的情境中不僅能借助方格圖數出三角形的面積,而且能依據三角形與平行四邊形之間的聯系算出三角形的面積,為學生探尋三角形的面積公式作鋪墊。
2.對活動設計的對比分析
《課標》指出:“教材應設計必要的數學活動,讓學生通過觀察、實驗、猜測、推理、交流、反思等,感悟知識的形成和應用。”人教版、蘇教版和青島版教材中探究活動的設計思路大致相同,都將三角形分成三類分別進行研究,最后歸納得到三角形的面積公式,這體現了分類和歸納的思想,但它們的側重點不一樣。
人教版教材設計的探究活動分三步進行。在提出探究問題后,啟發學生“能不能將三角形也轉化成學過的……”接著,引導學生用兩個完全一樣的三角形去拼平行四邊形,并得出結論“用兩個同樣的三角形可以拼出一個……”最后,依據轉化的過程推導出三角形的面積公式。蘇教版教材設計的探究活動側重下引導學生自主推導三角形的面積公式。在學生完成用兩個完全一樣的三角形拼平行四邊形的活動后,組織學生討論:(1)拼成平行四邊形的兩個三角形有什么關系?(2)拼成的平行四邊形的底和高與三角形的底和高有什么關系?每個三角形的面積與拼成的平行四邊形的面積呢?(3)根據平行四邊形的面積公式,怎樣求三角形的面積?通過這三個問題引導學生自主推導出三角形的面積公式。青島版教材中設計的探究活動側重于引導學生用數學的方式表達和思考,花了大量的篇幅用數學的方法分別演示將銳角三角形、直角三角形、鈍角三角形加倍轉化成平行四邊形的過程,并詳細地描述了由平行四邊形的面積公式推導出三角形的面積公式的推理過程。
與上述三種版本教材不同的是,北師大版教材在提出探究問題后,直接將情境中的三角形抽象為一般三角形,并通過加倍法將這個三角形轉化成平行四邊形和長方形,再依據平行四邊形和長方形的面積公式推導出三角形的面積公式(如圖2)。
四種版本教材中,北師大版教材設計的探究活動最為開放,最具有挑戰性,學生學習起來思維難度也較大,其他三種版本教材設計的探究活動則比較細膩,給學生提供了具體的方法引領。另外,人教版、蘇教版和青島版教材都將三角形加倍轉化成平行四邊形,而北師大版教材除了將三角形加倍轉化成平行四邊形外,還將三角形加倍轉化成長方形。
3.對文化滲透的對比分析
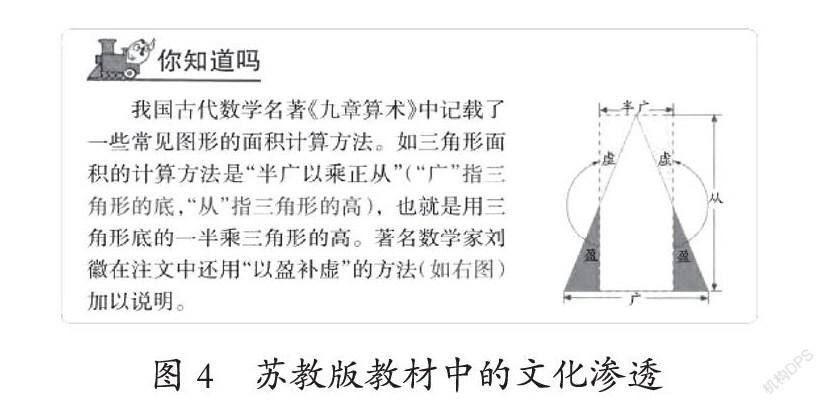
《課標》指出:“數學文化作為教材的組成部分,應滲透在整套教材中。”四種版教材中,人教版和蘇教版教材都注重數學文化的滲透,而北師大版和青島版教材對數學文化都未涉及。人教版教材在“你知道嗎”欄目中,向學生介紹了《九章算術》中的長方形和三角形的面積計算方法(如圖3)。蘇教版教材中,不僅向學生介紹《九章算術》中的三角形的面積計算方法,而且配以劉徽所著《九章注解》中“以盈補虛”的圖形,幫助學生理解“半廣以乘正從”的意思(如圖4)。
二、教學建議
1.情境創設從單元整體出發
數學知識具有整體性和結構性,每個知識點都處于一個相對穩定的系統之中。學生在數學學習過程中,不僅要掌握數學知識,而且要形成相應的認知結構。四種版本教材中“三角形的面積”的學習內容編排相似,這樣的安排雖然也能幫助學生形成認知結構,但如果從單元整體教學出發創設情境,將更有利于學生從整體上把握本單元的學習內容,形成整體認知。
比如,在教學本單元的起始課時可以創設這樣的情境:出示校園中一些區域的平面圖,其中有長方形、正方形、平行四邊形、三角形和梯形(甚至有組合圖形),讓學生分別求某些區域的面積。學生依據已有經驗自然會用公式求得長方形、正方形的面積。在求得這兩個圖形的面積后,教師順勢引導學生回顧得到這兩個面積公式的過程。隨后,再讓學生逐一思考怎樣求平行四邊形、三角形和梯形的面積,進行分課時教學。在分課時教學時,將此情境貫穿始終,后一課時在前一課時的基礎上進行。這樣就將“三角形的面積”置于“多邊形的面積”這個整體中,學生在學習“三角形的面積”時,既承接前面學習中獲得的知識經驗和思維經驗,又為后續學習梯形的面積積累新的經驗,在學習的過程中逐步形成良好的認知結構。
2.活動設計從已有經驗出發
學生學習的過程是經驗不斷積累的過程,新知的學習應建立在學生已有經驗的基礎上,這樣才能被學生深刻理解和掌握,并能在學習過程中催生新的經驗。因此,數學活動的設計應從學生的已有經驗出發。
在學習本課之前,學生在多邊形的面積計算方面已經具有的經驗是:通過鋪面積單位得到長方形和正方形的面積公式,以及將平行四邊形等積轉化成長方形得到平行四邊形的面積公式。這些經驗理應成為學生學習本課的基礎,但四種版本教材中,并沒有考慮學生的已有經驗。蘇教版教材中的例4直接暗示學生,兩個完全一樣的三角形可以拼成一個平行四邊形,而沒有給學生提供調用已有經驗的機會。其他三種版本教材雖然都提出了類似于“能把三角形轉化成學過的圖形嗎?”這樣的問題以激活學生的已有經驗,但學生依據已有經驗,能夠想到的是將三角形等積轉化成長方形或平行四邊形,而教材隨后設計的探究活動中卻是讓學生將三角形加倍轉化成平行四邊形或長方形,與學生的已有經驗脫鉤。
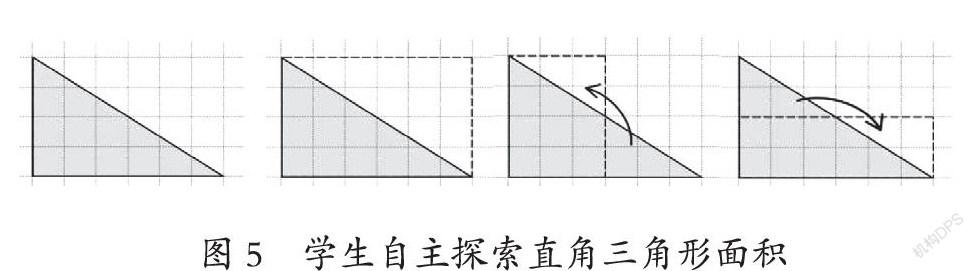
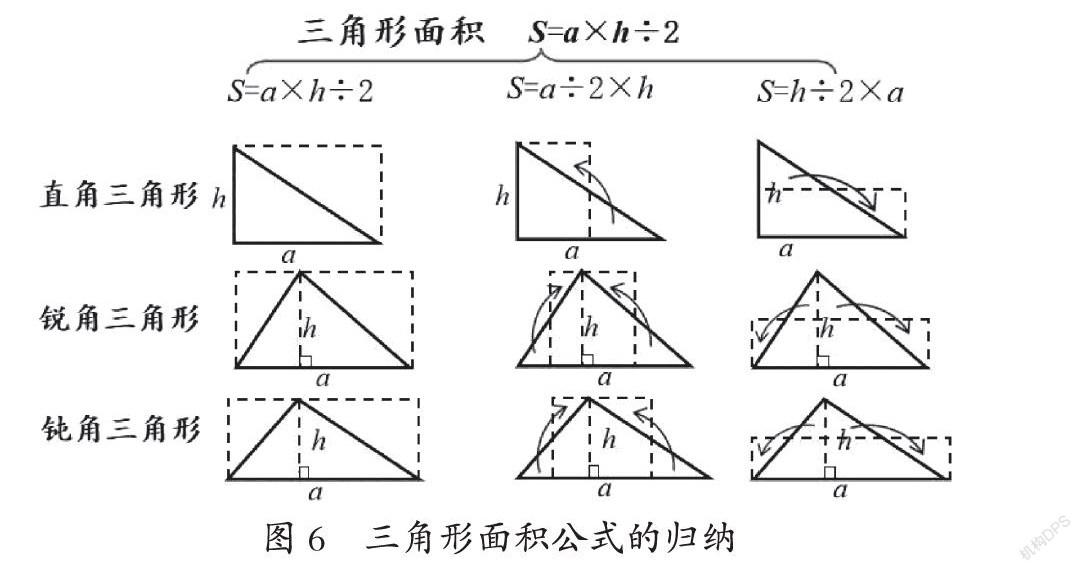
等積轉化雖然是學生的已有經驗,但用其來探尋三角形的面積公式思維難度較大,加上受課堂時間所限,所以四種版本教材都選擇了直接讓學生用加倍轉化這一相對簡單的方法探尋三角形的面積公式。其實,如果從關照學生的已有經驗、發展學生的思維能力,以及積累活動經驗的角度來看,完全可以讓學生依據已有經驗,自主探索三角形的面積公式。先讓學生求一個方格圖中的直角三角形的面積,學生除了能夠數出這個三角形的面積外,還會想到三種方法將這個三角形等積轉化成長方形,并算出面積(如圖5)。接著,學生可以利用前面活動中獲得的經驗,將一般直角三角形等積轉化成長方形,并得到直角三角形的面積計算方法,再依據直角三角形的面積計算方法類推銳角三角形和鈍角三角形的面積計算方法。根據“所有銳角三角形和鈍角三角形都可以沿高分成兩個直角三角形”,運用直角三角形的轉化方法將銳角三角形和鈍角三角形等積轉化成長方形,從而確定它們的面積計算方法。最后通過完全歸納得到三角形的面積公式(如圖6)。這樣從學生已有經驗出發設計的探究活動,相比四種版本教材中設計的探究活動需要更多的時間,但相對于學生的學習體驗與收獲來說是值得的。
3.文化滲透從意義理解出發
數學文化凝聚了古人的智慧與創造,在數學課中滲透數學文化能夠提升學生的素養,增長學生的智慧。雖然人教版和蘇教版教材都注重滲透數學文化,但它們所采用的方式是附加式,即在課的最后通過“你知道嗎”欄目向學生介紹《九章算術》中三角形的面積計算方法。但《九章算術》中三角形的面積計算方法是依據等積轉化得到的,與教材中的加倍轉化不一樣,學生對其只是了解,感悟是不深刻的,所以他們很難從中感受到古人發現的偉大,更談不上汲取智慧。
如果引導學生將探究三角形的面積公式的過程與古人發現三角形面積計算方法的過程結合起來,在經歷了上述探究過程后,再出示“你知道嗎”中的相關內容,學生不僅能夠理解《九章算術》中記載的三角形面積計算方法,而且能體會“以盈補虛”的價值,并將其用于梯形面積公式的探究過程中。學生不僅從中獲得數學知識,而且能夠感悟到古人的智慧與創造,獲得智慧的生長。
從學生立場出發,對多種版本教材中的同一內容進行橫向比較,能夠讓我們突破自身的經驗及思維定勢,發現更多的教學可能,從而為學生的學習提供更好的教學設計。
[責任編輯:陳國慶]

