數學深度學習的起源、內涵與教學策略

張俊忠　李艷琴

摘? ?要 深度學習是新課程理念下的重要及其學習方式。深度學習起源于美國，于2005年引入我國，在我國經歷近二十年的發展。根據中學數學的學科特征，給出深度學習的數學教學策略，可以為豐富和拓展深度學習研究提供參考。

關鍵詞 深度學習? 數學教學? 數學核心素養

2001年教育部發布《基礎教育課程改革綱要》，強調“要培養學生自主學習，鼓勵探究、質疑和討論，在教師主導下引導學生個性化學習。倡導科學精神，指導學生創新與實踐”。2020年國務院頒布《二〇三五年遠景目標建議》，提出“展望二〇三五年，建成文化強國、教育強國、人才強國。”要實現此目標，必須改進傳統講授式教學模式，創建新型學習方式，真正貫徹“自主、合作、探究”的學習方式。數學教學，必須圍繞“四基”，發展“四能”，通過深度學習養成數學核心素養，培養創新精神。

一、深度學習的起源

1956年，美國學者布魯姆在著作《教育目標分類》中，認為學習有深淺程度之分，最簡單的學習技能是機械記憶知識，最復雜的學習技能是評判觀點。1976年，美國學者馬頓和薩爾喬借鑒布魯姆認知分類理論，在論文《學習的本質區別：結果和過程》中首先提出教育學領域的深度學習概念，至此深度學習進入正式研究階段。1982年，澳大利亞學者比格斯與柯利斯提出SOLO分類法，根據復雜程度將學習結果分為五個層次，即前結構水平、單一結構水平、多層結構水平、關聯水平和擴展抽象水平，SOLO分類法使學習評價深入質的層面。1997年，美國學者恩特維斯托和拉姆斯登將深度學習的內涵延伸至學習的形成機制方面，認為只有通過深入探索，積極批判地思考，經歷長期專注的反思，才能實現深度學習。2006年，加拿大多倫多大學學者辛頓在雜志《科學》上刊登了有關深度學習的論文，在學術界激起了深度學習的研究浪潮。2016年，美國研究院分別從自我、人際和認知三個方向描述了深度學習的概念，創建了深度學習的能力結構框架。

國內深度學習的研究起步晚。2005年，上海師范大學學者何玲和黎加厚在國內期刊發表論文《促進學生深度學習》，第一次介紹深度學習的國際研究成果，并闡述了深度學習的特征。主張識記和理解從屬淺層學習，深度學習包括知識的應用、分析、綜合和評價，具備接受與批判、聯系與構建、應用與遷移的特點[1]。2006年，華中師范大學學者郭元祥在前期研究基礎上，發起了“海峽兩岸能力生根計劃”，推動以發展能力為目標的深度教學研究，主張提高學科能力，開展深度教學。2010年，國務院頒布文件《國家中長期教育改革和發展規劃綱要》，提出：只有實施深度學習，才能真正增強學生的創新能力和自主學習能力，至此國內開始廣泛地重視深度學習。2014年，為了推進培養學科核心素養，中國教育科學研究院學者田慧生帶領團隊進行深度學習的課題研究，指向提高知識遷移能力、深度理解能力和問顆解決能力。

二、深度學習的內涵

深度學習是發展學生批判思維和培養創新精神的學習，不僅關注積極的主動學習狀態，要靈活運用整合的知識和廣泛聯接的內容，實施觸類旁通的學習方法，還重視提高高階思維能力。根據布魯姆的分類方法，淺層學習的認知水平體現在識記和理解層次，是對知識的機械記憶或復制;深度學習的認知水平體現在應用、分析、綜合和評價層次。淺層學習在低認知水平，能夠獲得低認知技能，只需低階思維活動;深度學習在高認知水平，能夠獲得高認知技能，需要運用高階思維活動[2]。可以說，深度學習的本質特征是高階思維，培養和發展高階思維才能實現深度學習。

深度學習相對淺層學習和表面學習，是高質量的學習。深度是指直達事物屬性的程度，深度學習是指掌握、概括和運用本質的學習。不僅深度學習觸及學生作為人的根本部分，而且觸及知識的內部結構和本質屬性。學生作為人的根本部分是思想和靈魂，知識的本質屬性蘊藏于知識內核[3]。深度學習有六個方面的主要特征，即重視批判地理解、注重信息整合、關注知識建構、加強遷移運用、主張問題解決、倡導持續發展。

三、數學深度學習的教學策略

1.激發數學興趣，永葆學習動力

興趣是人對事物情感態度的體現，也是擁有持續內驅力的重要源頭。教育心理學研究表明，上課開始學生注意力比較集中，一般能夠持續15-25分鐘。數學內容比較抽象，理解掌握比較困難，如果教師上課沒有跌宕起伏，會讓學生覺得枯燥，那么學生更容易分散注意力。因此，數學教師要恰如其分利用幽默、風趣的語言，通過營造輕松有趣的氛圍，激發學生的數學熱情，啟發學生深入思考，持續保持數學學習的激情。

新課標指出：借鑒數學的發展歷史，重視數學文化，能夠豐富和拓展對數學的整體認識，將對數學學習起到促進作用。掌握數學史，將書本上的人物和思想變成生活中的小故事，體會數學的價值，讓學生感受到生活中無處不在的數學。歷史上數學家的故事，他們探索數學奧秘的艱難歷程，能夠讓學生感悟到數學知識的來之不易，從而珍惜學習機會。在數學教學中融入知識的產生背景，不僅開闊學生視野，豐富知識內涵，而且能夠解決疑慮，使得學生能夠深度欣賞和領悟數學，形成科學的數學觀。

2.實施變式教學，凸顯現象本質

在數學變式教學中，通過對數學概念、定理和習題等進行多層次、多角度的改變，應用多種方式，引導學生探索在“變”的過程中發現“不變”的因素，從“不變”中抓住本質，萬變不離其宗，從而深刻掌握事物的本質屬性[4]。數學變式教學的關鍵在于運用一系列的形式改變，展示數學知識的不同側面，從而揭示數學知識的全面結構，體現本質特征，這是促進學生深度學習數學的有效方法。

例1? 如圖1，在四邊形ABCD中，AB∥DC，E是BC的中點，若AE是∠BAD的平分線，試判斷AB，AD，DC之間的等量關系。

變式1：如圖2，在四邊形ABCD中，AB∥DC，AF與DC的延長線交于點F，E是BC的中點，若AE是∠BAF的平分線，試探究AB，AF，CF之間的等量關系。

變式2：如圖3，AB∥CF，AE與BC交于點E，BE：EC=2：3，點D在線段AE上，且∠EDF=∠BAE，試判斷AB、DF、CF之間的等量關系。

由圖1到圖3，圖形越來越復雜，條件越來越一般化。但是不管如何變化，三種狀態都有不變的因素，那就是都有平行關系與相等的角。在變化中的這個不變性，隱藏著這類問題的一般解決策略。如果有平行關系，可以考慮構造相似關系（全等是相似的特殊情況），將一些分散的條件集中在一起。如果有相等的角，可以考慮構造等腰三角形，凝聚條件。這樣就能夠在復雜的表象下，排除干擾，辨清方向，抓住關鍵。

3.通過問題解決，觸及深度思維

問題解決是以問題為線索，并將這一線索貫穿整個課堂的一種教學方式。教師先提出問題，學生帶著問題思考、分析、提問、討論，然后教師有針對性地啟發學生，循環往復，引導學生解決問題，最后抽象歸納。問題解決需要教師的主導身份和學生的主體角色始終處于一種動態的平衡狀態，因此教學前教師不僅要精心準備，而且在教學中要充分調動學生，適時調控課堂[5]。學生在經歷解決問題的具體過程中，體驗了數學新思想、新方法的產生過程，發展了數學高階思維，提高了創造力。

例2 今年是2021年，請你在兩分鐘內說出當x取何值時，y=|x-1|+|x-2|+…+|x-2021|有最小值？最小值是多少？

兩分鐘后，教師發現學生們幾乎都在利用分類討論的代數方法，通過去絕對值求最小值。利用此法，顯然兩分鐘內不可能解決。于是教師啟發學生，絕對值有代數意義，還有幾何意義，能否利用幾何意義？|x|的幾何意義是在數軸上表示數x的點與原點的距離，即|x|=|x-0|。這個結論可以推廣到|x1-x2|的幾何意義是在數軸上表示數的點和表示的點之間的距離。這時有學生提出問題，希望知道y的幾何意義。老師先讓學生回答這兩個問題：請說出y1=|x-1|+|x-2|和y2=|x+1|+|x+2|的幾何意義。y1的幾何意義，即在數軸上，表示數x的點與表示數1和表示數2這兩個點的距離之和。y2的幾何意義，即在數軸上，表示數x的點與表示數-1和表示數-2這兩個點的距離之和。老師又問x取何值時？y1和y2有最小值？最小值是多少？通過畫圖，學生們發現當1≤x≤2時，y1有最小值1;當-2≤x≤-1時，y2有最小值1。這時再請同學說出y的幾何意義，有學生迅速回答，即在數軸上，表示數x的點與表示數1、表示數2、…、表示數2021這2021個點的距離之和。再問：x取何值時？y有最小值？最小值是多少？通過畫圖，發現當x=1011時，y有最小值2+4+6+…+2020即1021110。有學生問x取何值時？y有最大值？通過畫圖，發現y沒有最大值。又有學生提問：如果有絕對值差的問題，能否用此方法？老師舉例z=|x-1|-|x-2|。請學生回答z的幾何意義。有學生回答，即在數軸上，表示數x的點和表示數1的點的距離，與表示數x的點和表示數2的點的距離之差。再請同學們回答z是否有最大值和最小值？有學生快速答出當x≤1時，z有最小值-1;當x≥時，z有最大值1。最后請學生們歸納這類問題的一般解決策略。

解含絕對值的問題，有代數方法和幾何方法。通過對絕對值幾何定義拓展，充分運用數形結合、分類討論等數學思想方法，利用圖形解決一類含絕對值的最值問題，方法簡潔明了。這是書本知識的延伸，也是數學方法的伸展。由特殊到一般，深度分析，不斷抽象概括，培養了學生的數學核心素養，提高了創造力。

4.踐行探究教學，培養創新精神

探究教學，就是開展探究為主的教學。在教師主導下，以學生自主、合作和探索學習為前提，以學生生活實際為背景，以教材作為主要探究內容，為學生提供展示、質疑和嘗試的多種機會，充分應用所學知識多元解決問題。不是把概念和策略直接告訴學生，而是教師通過創設一種師生、生生能夠自由平等交流的環境，在各種思想的碰撞中，學生不斷探索、自主發現，這是探究教學的本質特征[6]。探究教學關注開發學生的潛能，啟發學生深度思維，培養學生的創新意識，為終身可持續發展奠基。

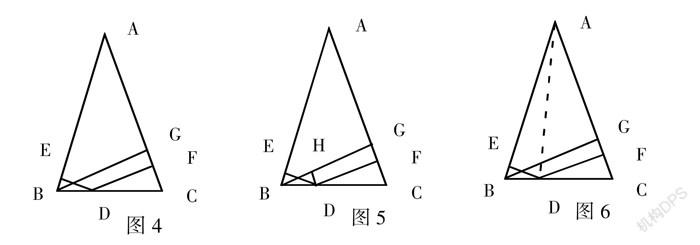
例3? 人教版初中數學教材習題：已知如圖4，在△ABC中，AB=AC，D是底邊BC上任意一點，DE⊥AB于E，DF⊥AC于F，BG是AC邊上的高，求證：DE+DF=BG

此題通常做法是截長補短。如圖5，過點D作DH⊥BG于H，則可以證明DF=HG，△BDE≌△DBH，故可以證明結論DE+DF=BG。此法是利用截長，然后啟發學生如何利用補短解決問題？是否還有其他方法？題設中有三條垂線段，垂線段與三角形的高有緊密聯系，能否考慮利用面積解決？有學生回答：如圖⑥連接AD，通過S△ABC=S△ABD+S△ACD，可以證明結論。這是面積法，利用圖形的面積關系，建立線段的等量關系。教師再提問，如果點D在CB的延長線上，這三條線段DE、DF、BG有何等量關系？有學生通過類比提出，如果點D在BC的延長線上，DE、DF、BG的等量關系應該是DE=DF+BG。

通過深入分析此題，除了利用常規方法解決，又學習了新方法即面積法。同時由靜態圖形拓展到動態圖形，滲透了動態幾何思想，培養學生善于用普遍聯系和運動變化的觀點認識事物。通過探究，深度挖掘，能夠提高學生的創造力，養成學生的科學精神。

任何教的問題都應以理解學為前提，否則教將成為無實際意義的活動。融入深度學習的數學教學策略應該在徹底掌握深度學習理論的基礎上，通過不斷調整淺層學習的思想和行為而逐步形成。堅持開展深度學習，才能真正實現素質教育和創新教育。

參考文獻

[1] 何玲，黎加厚.促進學生深度學習[J].計算機教與學，2005（05）：29-30.

[2] 劉偉，戚萬學，宋守君.致力于知識遷移的深度學習探究[J]現代教育技術，2019（03）：25-31.

[3] 張鵬，郭恩澤.指向“深度學習”的教學策略研究[J].教育科學研究，2017（09）：56-60.

[4] 劉長春，張文姊.中學數學變式教學與能力培養[M].濟南：山東教育出版社，2001：101-106.

[5] 張春莉.數學問題解決過程的內在心理機制[J].華東師范大學學報：教育科學版，1998（02）：57-65.

[6] 靳玉樂主編.探究教學論[M].重慶：西南師范大學出版社，2002：61-70.

[作者：張俊忠（1971-），男，湖北應城人，貴州師范學院數學與大數據學院，副教授，碩士生導師，博士;李艷琴（1982-），女，貴州思南人，貴州師范數學與大數據學院，教授，碩士生導師，博士。]

【責任編輯? 郭振玲】

*該文為貴州省教育科學規劃課題”數學史融入高等代數教學研究“（2021B230）;貴州師范學院教學內容和課程體系改革項目“新時代高校課程思政建設與實踐研究—以《高等代數》為例”（2020JG04）的研究成果