信息化視角下網絡畫板在高中數學函數教學中的實踐
王志堅
【摘要】本文旨在闡述以希沃一體機與網絡畫板(離線播放器)為主要教學設備,開展《任意角的三角函數》的教學活動。筆者通過動態演示,輔助學生進行數學思維,理解任意角與單位圓交點,建立三角函數與交點坐標的一一對應關系,從而讓學生形成三角函數的數學概念,并更好地發現三角函數的規律性。
【關鍵詞】網絡畫板;高中數學;三角函數
在信息化2.0的背景下,高中數學教學應當有效應用計算機信息技術,逐步實現高中數學信息化教學,幫助學生理解透徹所學到的數學知識,落實高中數學學科核心素養,從而提高學生的數學學習成績,保障高中數學教學質量。三角函數是高中數學最重要的函數之一,是最典型的周期函數,是描述客觀世界中表現周期現象變化規律的基本數學模型,在提升學生數學抽象邏輯推理、數學建模、直觀想象、數學運算、數據分析等素養上也具有不可替代的重要作用。在思想方法上,本設計著重概念的形成,通過分析、探究、概括思維的邏輯加工,依據已有三角函數的知識基礎,重新認識任意角三角函數的定義,并在后續的解題上,強化定義的形成和運用。作為《任意角的三角函數》的教學重點,任意角三角函數的定義將貫穿課程始終。從單位元的出現,到終邊交點坐標與函數之間的聯系。與已有經驗不同,三角函數的對應關系不以“代數運算”為媒介,而是以“幾何元素之間的對應”,強調三角函數得到的過程,最終形成定義。網絡畫板是專業的數學教學平臺,為教師和學生提供一個操作的環境,讓數學真正動起來。通過互聯網,廣大教師在平臺上共享課件資源,并根據自己的教學需要重新編輯制作。學生也能夠利用網絡畫板進行自主探究,培養學習數學的興趣。基于上述背景,筆者決定使用網絡畫板進行三角函數的輔助教學。
一、具體實施
1.教學問題診斷
已有的基礎知識可能成為本節知識學習的羈絆。一方面,初中階段我們已經在直角三角形的前提下,初步掌握了三角函數中正弦、余弦、正切的定義,即直角三角形中的各邊比值。而在本節內容學習中,由于角的范圍拓展,三角函數無法通過直角三角形給予更多的支持,同時定義也由原來的“邊的比值”變為“坐標的對應關系”,這在理解上讓學生很難轉變,乃至部分學生始終希望能讓三角函數的定義回歸到“邊的比值”上,無法完成本節課程的內容學習。另一方面,在本冊書中,我們先后學習了函數的性質及包括指數函數、對數函數等初等函數,確定了“以代數運算”為媒介的學習載體。而本節內容,三角函數的建立以“幾何元素之間的對應”為模型,這在認識上必須采取措施破除定勢,幫助學生搞清楚三角函數的“三要素”,特別是要先明確“給定一個角,如何得到對應的三角函數值”的操作過程,從而得出定義。
2.溫故知新
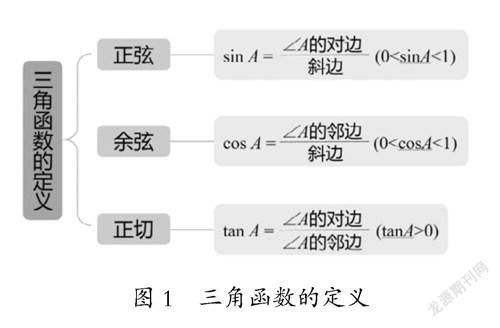
以初中已有三角函數定義為基礎,說明已有知識基礎對于任意角的限制,引出本節課程內容學習的必要性。如圖1。
3.以自然現象為背景,引入任意角三角函數概念
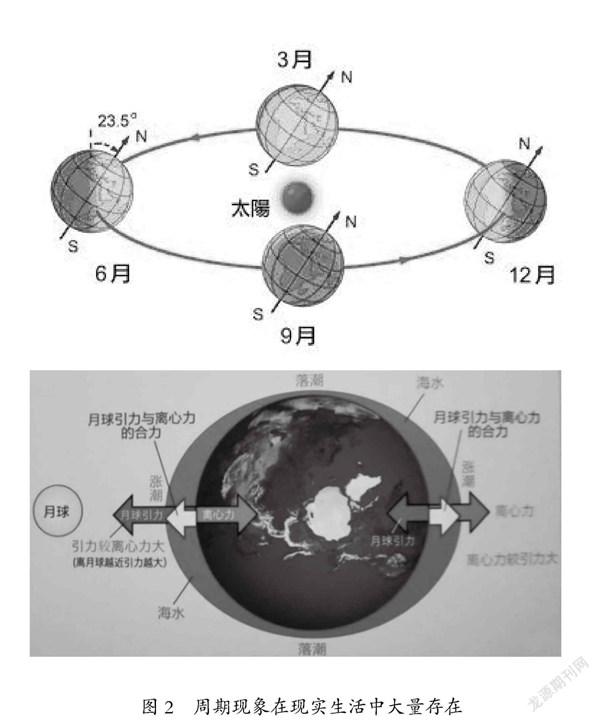
筆者以PPT觀察為教學活動(四季更替、潮汐現象),提出問題,引出學生了解“周期現象在現實生活中大量存在”,從而引入任意角三角函數概念。如圖2。
4. 概念生成,引入網絡畫板輔助教學
引入單位圓,并將角放置于單位圓中,終邊與單位圓產生。此過程中特別需要強調“一一對應”—即角、終邊、終邊與單位圓交點及其坐標均唯一。根據角的范圍擴充,我們需要一個一般性的方法來重新定義三角函數。通過在直角坐標系中角的終邊與單位圓的交點,我們可以建立三角函數的模型,并通過交點坐標,從而言之有物地刻畫出三角函數的定義。
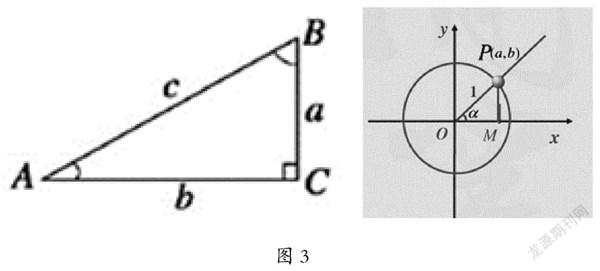
以銳角情況為基礎,給出三角函數定義,繼而推廣到任意角。思考:如圖3,RT△ABC中,∠C=90°,若已知a=3,試求sinA,cosA,tanA的值。
解:由初中已掌握直角三角形中三角函數的定義,sinA=a/c=3/5,cosA=b/c=4/5,tanA=a/b=3/4
思考:銳角三角函數(在單位圓中)若|OP|=r=1,則以原點O為圓心,以單位長度為半徑的圓,稱為單位圓。
sinα=MP/OP=b? cosα=OP/OP=a? tanα=MP/OM=b/a
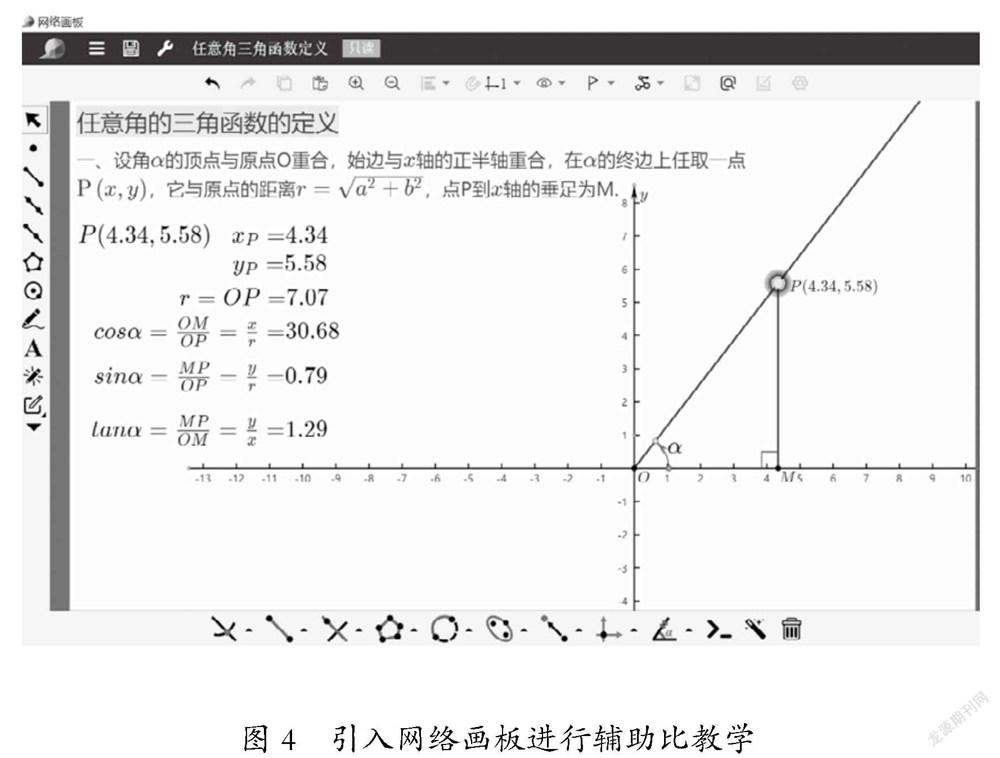
然而,學生對引入單位圓的原因難以理解,傳統地使用畫圖的方法難以讓學生深度學習本節課的知識。因此,筆者引入網絡畫板進行輔助。利用網絡畫板的軌跡、計算、旋轉、跟蹤功能,能夠將曲線較為準確、直觀地展示出來,體會數形結合的思想。如圖4。在明確三角函數定義的基礎上,依據交點坐標與函數的關系,我們可以有效地探討三角函數的對應關系,包括符號的判斷。角在不同象限對于三角函數值變化的影響,配以動態過程演示,強化三角函數的定義及相關簡單性質的理解。
5.學生反饋與教師反思
課后,教師對學生進行問卷調查,并根據學生的學習成果進行反思,對網絡畫板的應用進行修改。
二、教學成效
1.實施效果
課堂效果整體情況:本節課在A班共52名同學參與,使用了網絡畫板進行輔助教學,通過課堂作業反饋,有46名同學能正確完成課堂練習題目,正確率達到88.46%。另有一節在B班的同課異構課,沒有使用網絡畫板進行輔助,參與課堂的同學為49名,能正確完成課堂練習題目的同學有36名,正確率為73.47%。
課后作業:A班測試卷滿分100,平均分81.2分;B班測試卷滿分100分,平均分71.9分。
2.應用前景
從上述課堂實踐和課后作業表明,網絡畫板可以幫助學生強化“一個角,一個三角函數值”的對應關系,區別與一次函數、二次函數的“代數運算”。三角函數強調的是幾何要素關系,在一般函數概念引導下的“下位學習”,由三角函數對應關系的獨特性,讓學生再一次認識函數的本質。
因此,本節課的實施效果證明了網絡畫板對于高中數學函數教學是可行的。在信息化教學2.0的背景下,以信息技術手段為載體,通過對網絡畫板的合理利用,能幫助學生落實數學建模能力,提高高中學生數學學科的核心素養。
未來,我們將在校內推廣網絡畫板,著重幫助高二、高三的學生突破學科上的教學難點。
參考文獻:
[1]尹潔,侯小華.網絡畫板在高中函數教學中的應用[J].中國教育技術裝備,2020(13):36-37.
[2]潘曉清.核心素養導向下的高中數學信息化教學研究[J].中國新通信,2021,23(18):210-211.
[3]布瑞昌,劉帥,吳惠貞.基于SPOC的化學學科有效教學模式的實踐研究[J].化學教與學,2022(4):22-24.

