創設問題情境 發展科學思維

楊換換

【摘? 要】發展學生的科學思維是物理教學的重要教學目標之一，也是教學改革的難點，因此，發展學生科學思維越來越受到教師的關注。創設問題情境在初中物理教學中已經成為發展學生科學思維的有效載體，由此本文通過創設適當的問題情境，在教師問題鏈的引導下促進學生對知識的深刻理解，同時發展學生的科學思維。

【關鍵詞】科學思維;創設情境;初中物理

一、問題的提出

科學思維是物理核心素養的重要內容，發展物理核心素養的關鍵是發展學生的科學思維能力，在教學中創設問題情境對培養學生的科學思維能力有關鍵作用。建構物理模型是科學思維的重要內容之一，因此，本文將問題情境的創設轉化為物理模型的建構。

力學綜合題在初中物理學中是學生學習的重點和難點，學生認為力學綜合題難學的主要原因：知識之間的聯系較多，出現的物理過程較多，需要較強的提取信息的能力和科學思維能力。雖然力學綜合題很難學，但它卻是發展學生科學思維很好的載體。

為此，本文以初中力學綜合題為例，以問題情境為探究的載體，培養學生的科學思維能力。

二、教學設計思路

力學綜合題是初三物理的專題復習課，學生已經有了力學的相關概念，但這些概念可能是零散的。筆者所在學校位于偏遠鄉鎮，學生的學習能力普遍較弱。因此，筆者在仔細研讀課程標準和教材的前提下為解決力學綜合題，讓學生吃透簡單題，將力學知識聯系起來，把問題情境轉化為建構物理模型，擬建立起學生處理力學綜合題的基本思維路徑，從而發展學生的科學思維能力。

本文對物理教學過程進行了優化，其主要特征就是對學生的思維過程顯性化。教師以有層次、有梯度的問題鏈展開教學，讓學生經歷將問題情境轉化為物理模型的過程，經歷科學推理、科學論證等具體的思維活動。學生明確并經歷這些思維活動，能夠提升自己的科學思維能力。

（一）問題情境為教學載體

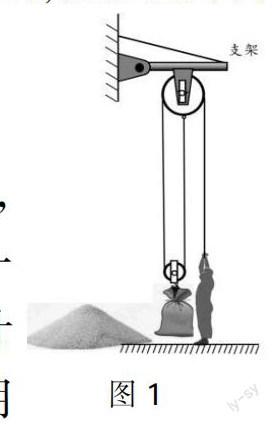
以農村蓋房子為例，如圖1所示，已知支架和繩子能承受的最大力是一定的，且已知拉力和沙子重力，如何計算動滑輪重力？為了保證安全，工人用此滑輪組可以達到的最大機械效率是多少呢？

學生對這樣的情境較為熟悉，但并不會分析這樣的實際問題，通過這樣的問題情境容易引發學生對生活實際問題的關注和思考。

（二）顯性化思維過程

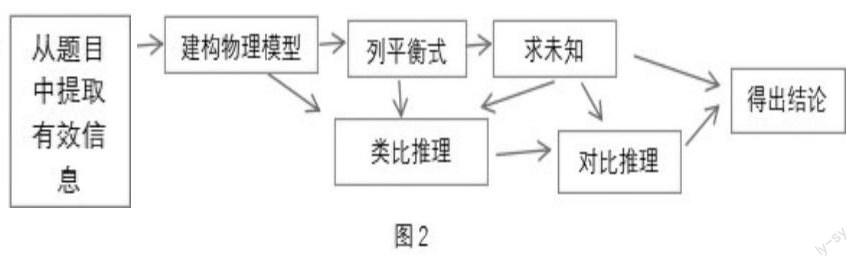
以農村蓋房子所用的滑輪組為主問題貫穿教學，將問題拆分成幾個問題鏈進行分析，通過引導學生分析問題、解決問題發展思維能力。整體教學思維如圖2所示。

三、創設問題情境，發展科學思維

創設情境是解決具體問題的關鍵，通過問題的解決可以促進學生科學思維能力的養成。

（一）教師引導，總結解題方法

問題情境1：如圖3所示，人重550 N，繩子對人的拉力為250 N，根據人受力示意圖，求地面對人的支持力。

教學過程：

（1）提取關鍵信息，確定研究對象。

師：通過讀題找到此題中的研究對象。

生：是人。

（2）建構物理模型。

師：將人隔離出來進行受力分析。

生：如圖3所示。

（3）進行科學推理。

師：請根據運動和力的關系列平衡式。

生：G=F+F支

（4）得出結論。

師：請你算出支持力的大小。

生：F支=G-F=550 N-250 N=300 N。

師生總結解題思路：提取關鍵信息將問題情境轉化為物理模型;列平衡式求未知。

師：請同學們思考繩子對人的最大拉力是多少？為什么呢？

生：是550 N，如果繩子拉力大于550 N，支持力為零，人會被拉到空中。

教師總結：我們學習了簡單力學題的基本解題方法，這個過程中體現了簡單計算題的基本思維路徑，希望同學們養成嚴密的邏輯思維習慣。

設計意圖：在此教學過程中，將實際問題情境與物理知識相聯系，通過建構物理模型，分析問題、科學推理從而解決問題，發展了學生的科學思維能力。

（二）利用所學方法解決簡單力學問題

問題情境2：如圖1所示，滑輪組懸掛在水平支架上，某工人站在水平地面上，豎直向下拉動繩子自由端，使物體A勻速上升。已知物體A重400 N，繩子對人的拉力為250 N，兩個滑輪質量相等，不計滑輪組的繩重和摩擦。求：

（1）動滑輪的重力G輪。

（2）勻速提升物體A時，求出支架對定滑輪的拉力T。

教學過程：

師：請同學們根據剛才所學習的解決問題的方法計算本題。（15 min）

生：獨立思考（5 min），小組討論，分析、畫圖、計算得出結論。

小組代表展示結果。

生：（1）提取有效信息找到研究對象動滑輪G輪，將其隔離進行受力分析，如圖4所示，根據運動和力的關系列平衡式：G輪+GA=2F。將平衡式變形求出動滑輪重力：G輪=2F-GA=2×250 N-400 N=100 N。

（2）同理：提取有效信息找到研究對象定滑輪G輪，將其隔離進行受力分析如圖5所示，根據運動和力的關系列平衡式：T=G輪+3F。將平衡式變形求出支架對定滑輪的拉力：T=G輪+3F=100 N+3×250 N=850 N。

師：若支架能承受的最大力為1 600 N，那么此時繩子的拉力是多少呢？

生：將平衡式T=G輪+3F變形求繩子拉力F=（T-

G輪）/3=（1 600 N-100 N）/3=500 N。

教師總結：非常好，同學們通過獨立審題抓住關鍵信息，找到研究對象，建構物理模型，分析推理得出了結論。同學們養成“一情境一圖，一圖一方程”的解題習慣，這個過程體現了建立模型和科學推理的過程。

設計意圖：學生通過所學物理知識能夠獨立地經歷提取信息—物理情境—物理模型—分析推理—得出結論的過程。此過程可以發展學生的科學思維能力。

（三）解決力學綜合問題

問題情境3：如圖1所示，農村蓋房時，要把沙子裝到麻袋里（麻袋質量不計，一次可裝重2 000 N的沙子），用滑輪組將沙子提升到屋頂。工地有2 t沙子，工人站在水平地面上，豎直向下拉動繩子自由端，使400 N的沙子勻速上升，提升過程中繩子的拉力為250 N。已知兩個滑輪質量相等，不計滑輪組的繩重和摩擦。求：（1）求動滑輪的重力;（2）在保證安全的前提下，水平支架可承載力為1 600 N，繩能承受的最大拉力800 N，工人重550 N。求工人用此滑輪組可以達到的最大機械效率。

（1）通過提取關鍵信息，確定解題思路。

師：提取有效信息：支架可承受的最大力1 600 N，繩能承受的最大拉力800 N，工人重550 N，麻袋可裝的沙子的最大重是2 000 N。以上四種情況都害怕超過對應的最大值，什么情況下就安全了呢？學生小組討論。

生：當四種情況都安全的時候，整個裝置才能安全。

師：四種情況都不能超過最大值，那如何比較呢？我們求出四種情況對應的繩子的最大拉力即可。現在請同學們計算四種情況下繩子的最大拉力。學生小組討論。

（2）根據解題思路，交流討論，確定解題過程。

師：同學們發現什么了嗎？這道綜合題其實就是以上幾個簡單題的綜合，一般力學綜合題難就難在物理過程較多，只需要將其拆分成一個個簡單題，再對比分析推理即可得出結論。

學生小組代表展示：繩能承受的最大拉力800 N，工人重550 N，繩子的最大拉力為550 N，在上題中支架承受最大力1 600 N時對應的繩子的最大拉力為500 N。當計算麻袋裝重不能超過2 000 N時對應的繩子的最大力時，將動滑輪隔離受力分析如圖4所示，列平衡式：2F=G輪+GA。在上題中已經求得動滑輪重G輪=100 N，計算出此時繩子的拉力為1 050 N。在保證所有情況都安全的前提下，繩子的最大拉力不能超過500 N。

師：在保證裝置安全的前提下如何計算最大機械效率呢？

生：繩子的最大力為500 N時，提升的沙子最重，算出機械效率最大。以動滑輪為研究對象列平衡式：G輪+GA=2F，計算此時物重為GA=2F-G輪=2×500 N-100 N=900 N。η=GA/nF=900 N/2×500 N=90%。

（3）教師總結：我們通過審題，抓住其中的關鍵信息，理清了解題思路，將知識與多個物理過程聯系起來，通過對比分析、類比推理等過程得出結論。這體現了建構模型和科學推理的過程。

設計意圖：這是一道較為復雜的力學綜合題，意在讓學生知道復雜的力學綜合題一般是由多個簡單題組合而成，我們在計算時將復雜綜合題拆分成一道道簡單題。在保證安全的前提下，繩子怕斷、支架怕斷、人怕吊起來、麻袋怕破。當繩子、支架、人、麻袋都安全的情況下才能保證裝置安全。引導學生考慮問題要全面，在解題過程中有建立物理模型、對比分析、類比推理等過程，學生將知識聯系起來解決實際問題，發展了學生的科學思維能力，落實了從物理走向社會的教學理念。

（4）應用知識解決問題。

問題情境4：為了說明分子之間有引力，小明在實驗室用兩個緊壓在一起的鉛柱做實驗，如圖6所示，兩個鉛柱沒有被拉開，判斷小明做的鉛柱實驗能否說明分子之間存在引力。請寫出推理過程。（該實驗室的大氣壓為1×105 Pa。）

物理模型建構：將以上問題情境轉化為物理模型，以鉛柱B為研究對象，隔離受力分析（圖7）。鉛柱B受到自身重力GB和桶對其的拉力G桶，向上的大氣壓力F大氣和向上的分子間引力F引（不確定）。

科學論證過程：對此物理模型進行分析，若大氣壓力F大氣大于或等于鉛塊B重力GB與桶重G桶的和，則僅靠大氣兩鉛柱也無法拉開，該實驗不能證明分子之間有引力;若大氣壓力F大氣小于鉛柱B重力GB與桶重G桶的和，則向上的重力除大氣壓力外還須有分子間引力，可以證明分子間存在引力。

在此過程中學生將問題情境轉化為物理模型，并對其進行分析論證，這個過程可以有效培養學生的科學論證能力。

總之，在物理教學中，本文以物理情境為探究的載體，將物理情境轉化為物理模型，通過顯性化的科學推理或者科學論證過程得出結論。在整個教學過程中，學生用所學物理知識解決實際問題，同時也有效培養了學生模型建構、科學推理、科學論證等科學思維能力。

【參考文獻】

[1]中華人民共和國教育部.普通高中物理課程標準（2017年版）[M].北京：人民教育出版社，2018：51-53.

[2]陳運保，劉青.指向科學思維的高中物理教學設計——以“曲線運動”為例[J].物理教師，2020，41（8）：25-29.