運(yùn)用動(dòng)靜結(jié)合策略解初中數(shù)學(xué)平面幾何動(dòng)點(diǎn)問題

摘 要：平面幾何是初中數(shù)學(xué)中的重點(diǎn)內(nèi)容之一.其中，動(dòng)點(diǎn)問題常常在中考數(shù)學(xué)中作為壓軸題出現(xiàn)，這類試題能有效考查學(xué)生分析和解決問題的能力，較好地滲透了分類討論、數(shù)形結(jié)合、化歸等數(shù)學(xué)思想.動(dòng)點(diǎn)問題較為復(fù)雜，導(dǎo)致很多學(xué)生遇到相關(guān)題目時(shí)無法及時(shí)找到解題思路.為了幫助學(xué)生提高解題能力，本文對(duì)中考中平面幾何動(dòng)點(diǎn)問題常考的兩大類題型，以2021年兩道中考題為例加以分析，并向?qū)W生講解相關(guān)的解題策略.

關(guān)鍵詞：平面幾何；動(dòng)點(diǎn)；初中數(shù)學(xué)

中圖分類號(hào)：G632 文獻(xiàn)標(biāo)識(shí)碼：A 文章編號(hào)：1008-0333（2023）08-0029-03

1 “化動(dòng)為靜”——?jiǎng)舆呣D(zhuǎn)移求解范圍問題

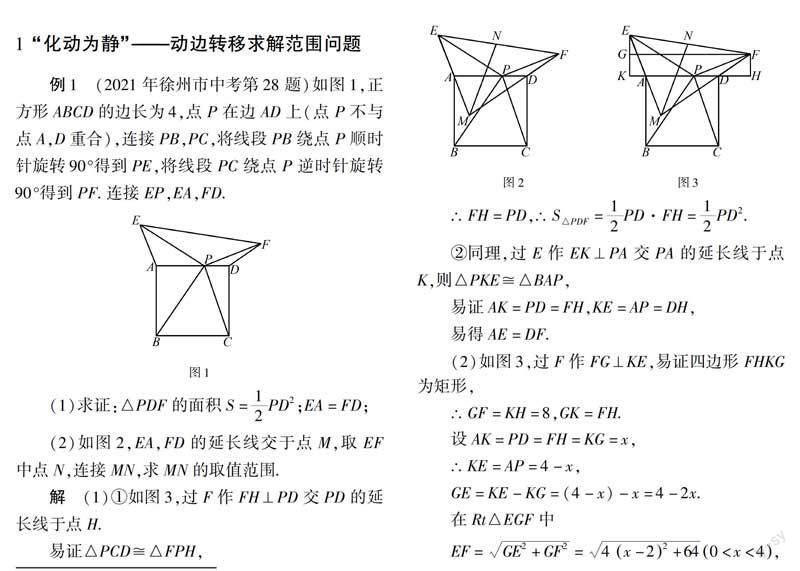
例1 （2021年徐州市中考第28題）如圖1，正方形ABCD的邊長(zhǎng)為4，點(diǎn)P在邊AD上（點(diǎn)P不與點(diǎn)A，D重合），連接PB，PC，將線段PB繞點(diǎn)P順時(shí)針旋轉(zhuǎn)90°得到PE，將線段PC繞點(diǎn)P逆時(shí)針旋轉(zhuǎn)90°得到PF.連接EP，EA，F(xiàn)D.

3 反思總結(jié)，提高學(xué)生解題能力

對(duì)于動(dòng)點(diǎn)問題，學(xué)生首先要能夠明辨題目中的變量和不變量.只有分清楚變量和不變量才能夠化動(dòng)為靜，將所求的變量轉(zhuǎn)化到恒定的不變量上.具體問題中通常是將運(yùn)動(dòng)的點(diǎn)或邊，轉(zhuǎn)移到不變的邊上，這樣問題也就迎刃而解了.其次，動(dòng)點(diǎn)在運(yùn)動(dòng)過程中的特殊點(diǎn)，也是解題的突破口之一，要抓住關(guān)鍵點(diǎn)，將一般情況特殊化，觀察運(yùn)動(dòng)過程，進(jìn)而能夠發(fā)現(xiàn)動(dòng)點(diǎn)的運(yùn)動(dòng)規(guī)律.對(duì)于與函數(shù)有關(guān)的動(dòng)點(diǎn)問題，要嘗試建立動(dòng)點(diǎn)運(yùn)動(dòng)過程中的函數(shù)關(guān)系，利用函數(shù)性質(zhì)進(jìn)行求解.

只要掌握了動(dòng)點(diǎn)問題的解題策略，不論動(dòng)點(diǎn)怎么動(dòng)，我們都能以不變應(yīng)萬變，順利求解此類試題.動(dòng)點(diǎn)問題常常較為綜合，求解過程也要運(yùn)用多種數(shù)學(xué)知識(shí)，所以能有效地考查學(xué)生的數(shù)學(xué)知識(shí)和數(shù)學(xué)能力，有效區(qū)分不同考生的數(shù)學(xué)學(xué)習(xí)水平，為中學(xué)階段的選拔提供一定依據(jù).

教師在教學(xué)中要注意培養(yǎng)學(xué)生的幾何素養(yǎng)，有意訓(xùn)練學(xué)生的動(dòng)態(tài)思維，將動(dòng)點(diǎn)問題中的“動(dòng)”與條件中的“靜”結(jié)合起來，學(xué)會(huì)運(yùn)用數(shù)形結(jié)合等數(shù)學(xué)思想方法，再結(jié)合專項(xiàng)訓(xùn)練，一定可以提高學(xué)生對(duì)動(dòng)點(diǎn)問題的求解能力.

參考文獻(xiàn)：

［1］王中文.初中數(shù)學(xué)動(dòng)點(diǎn)問題的解題策略[J].讀與寫（教育教學(xué)刊），2012，9（03）：115.

[2] 陳韌.初中數(shù)學(xué)動(dòng)點(diǎn)問題的解題策略分析[J].課程教育研究，2018（06）：143-144.

［責(zé)任編輯：李 璟］

收稿日期：2022-12-15

作者簡(jiǎn)介：蘇雅（1998.7-），女，研究生，從事初中數(shù)學(xué)教學(xué)研究.