“雙減”背景下初中數學單元作業設計的策略

劉燕　連麗萍

摘要：為了落實國家的“雙減”政策，落實減負提質增效，數學教師應當設計一系列能激發學生思維和主觀能動性的作業，為培養數學核心素養服務.筆者以八年級下學期數學第十九章《一次函數》為例，從關注數學文化，引導文獻檢索；深化核心知識，優化層級作業；提升信息素養，促進學科融合；展示數學價值，創設實踐活動等四個維度探索數學單元作業設計的策略，促進學生數學核心素養的發展.

關鍵詞：雙減；單元作業設計；數學核心素養

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2023）08-0020-03

“雙減”政策頒布實施后，作為數學教師應當認真思考從“量”和“質”上轉變作業布置模式，優化學生數學作業，讓作業發揮培根鑄魂、啟智增慧的作用.因此，數學教師應當設計一系列能激發學生思維和主觀能動性的作業，以提升學生的數學核心素養，切實保證將“減負提質”落到實處，為此筆者以八年級下學期數學第十九章《一次函數》為例，探索數學單元作業設計的策略.1關注數學文化，引導文獻檢索

“數學實力往往影響著國家實力，幾乎所有的重大發現都與數學的發展與進步相關.”解析幾何是通過建立坐標系，把幾何和代數聯系起來，利用代數工具解決幾何問題.它的起源可以追溯到古希臘數學家對圓錐曲線的研究.法國數學家笛卡兒首先引入了坐標系，牛頓、歐拉、拉格朗日等人對解析幾何的發展也發揮了重要作用.

在七年級下冊，學生們學習了平面直角坐標系，到本章學習一次函數，學生對解析幾何有比較粗淺的體會，但是為什么要建立解析幾何？它對于數學和現實世界的發展起了什么樣的作用？中國數學家對此研究有何貢獻等一系列問題接踵而至，教師們除了在課堂上可以做一個簡要的介紹，還可以在單元作業中提供相關閱讀材料，讓學生認識到數學發展的來龍去脈，逐步培養學生對數學的好奇心和求知欲.

2深化核心知識，優化層級作業

義務教育數學課程以習近平新時代中國特色社會主義思想為指導，要讓每個學生都能獲得良好的數學教育，不同的學生在數學上得到不同的發展.

“雙減”政策鼓勵布置分層、彈性、個性化作業.科學合理的層級作業可以兼顧到每一個學生，主要從作業難度和作業量兩個維度加以考量.從作業難度分析，作業要由淺入深，給不同的人不同的作業.按照作業的難易水平將作業分成不同的層級.第一層是基礎題型；第二層是能力提升題型，難度略高于第一層題，但大部分學生經過思考可以獨立完成；第三層是開放創新題型，難度高于第一二層，需要透徹理解，發散思維，才能完成.從作業量分析，基礎不扎實的學生只需完成第一層題，檢驗學生對基本概念、原理、法則、定理等知識的應用能力；對于具有一定的學習能力的學生完成第一二層題，考查學生對基本概念和基本原理遷移的應用；對于學習能力強的學生應選擇難度高于學生原有水平的，因此，可以只完成第二三層題，考查學生對知識深度加工的能力，培養學生數學思維的靈活性和獨創性.

例如，一次函數的定義、圖象和性質是本章的主要基礎知識，根據題目的條件求一次函數解析式，畫出圖象，了解性質是本章的基本技能.因此在單元作業設計中要注意體現“雙基”.但函數的內容具有一定的抽象性，數形結合的思想方法是本章的重點也是難點.因此在設計單元作業時除了要讓大部分學生掌握“雙基”，還要讓優等生的潛力有更大的發揮空間.因此，可以設計層級作業如下：

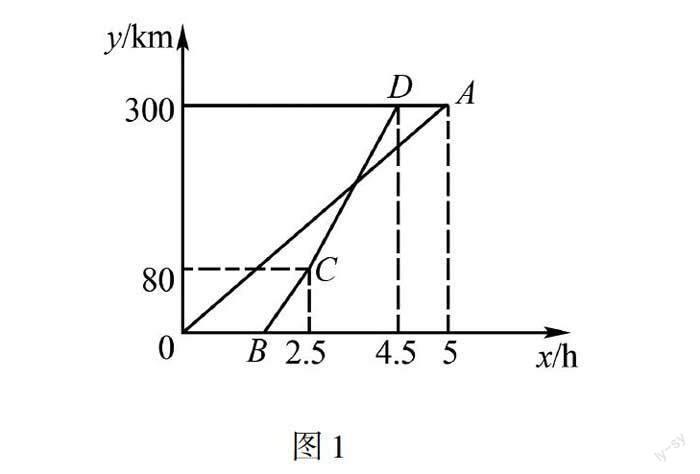
例1浙江金華與上海相距300km，甲乙兩車先后從金華出發前往上海，乙車比甲車晚出發1.5h，如圖1，線段OA表示甲車離金華的距離ykm與時間xh之間的函數關系；折線BCD表示乙車離金華的距離ykm與時間xh之間的函數關系．請根據圖象解答下列問題：

問題1甲車的速度是km/h，點B的坐標為；

問題2乙車到達上海時，求甲車與金華的距離；

問題3求CD線段的函數表達式；

問題4求出甲車和乙車離金華的距離y1、y2與時間x之間的函數關系式；

問題5乙車行駛多久后，兩車距離15km？對于學習后進的學生只要求完成問題1～4，對于中等生要求完成問題1～5，對于優等生要求完成問題3～5，還可以要求他們發散思維，結合題意看看還能提出什么問題，并完成解答.

以下問題6～8就是在教學實踐中，由學生提出的.

問題6在乙車行駛過程中，乙車行駛多久能追上甲車？

問題7結合圖象，回答：

當時，甲車離出發點更遠；

當時，乙車離出發點更遠；

問題8如果乙車保持剛開始的速度勻速行駛，能否在甲車到達上海之前追上甲車.

這樣的層級作業滿足了學生們個性化的需求，讓后進生不掉隊，讓中等生得到鞏固提升，讓優等生探索知識的能力得到培養，考查了學生的創新能力和創新意識.“雙減”政策要求做強做優免費線上學習服務，因此對于較難的題目，教師可以制作微課，讓有需要的學生掃二維碼即可觀看.

3提升信息素養，促進學科融合

課程標準指出要創設合理的信息化學習環境，提升學生的探究熱情，提高學生的信息素養.課本19.2.2的例2，讓學生畫出y=-6x與y=-6x+5的圖象，通過觀察圖象得到一次函數y=kx+b（k≠0）的圖象與直線y=kx（k≠0）的關系.學生發現當k相等時，兩直線的傾斜程度相同，自然而然就想進一步探索k與直線傾斜程度的關系.因此，在單元作業中可以設計利用信息技術解決以下問題.

例2（1）利用幾何畫板軟件畫出y=x+1，y=2.3x+1，y=5.8x+1，y=7.9x+1的圖象，觀察圖象，說說當k>0時，k對圖象傾斜程度的影響.

（2）利用幾何畫板軟件畫出y=-x+1，y=-2.3x+1，y=-5.8x+1，y=-7.9x+1的圖象，觀察圖象，說說當k<0時，k對圖象傾斜程度的影響.

（3）觀察以上函數圖象，說說k互為相反數時，圖象的特點.

這道數學與信息技術相融合的作業，讓學生借助信息技術手段，對課內的知識進行延伸，為高中解析幾何的深入學習做了鋪墊.在實際問題解決中，教師應善于利用現代信息技術，設計信息化的數學作業，增強學生的探究熱情，開闊學生的數學視野，促進信息技術與數學課程的融合.

4展示數學價值，創設實踐活動

“數學已成為航空航天、國防安全、生物醫藥、信息、能源、海洋、人工智能、先進制造等領域不可或缺的重要支撐”.數學的應用滲透到現代社會的各個方面.函數在研究自然界和現實生活中的變化規律及解決相關問題中有著廣泛的應用.因此，教師在單元作業中可設計實踐活動作業，以選擇方案為問題情境，讓學生用一次函數的知識解決方案優選問題，體會函數模型思想，提高運用函數的知識分析、解決實際問題的能力［1］.例如，可以設計實踐活動作業如下：

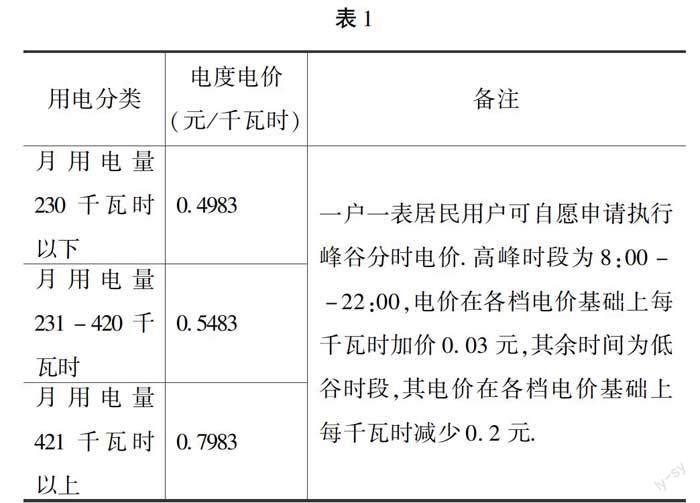
例3以福州居民“一戶一表”用戶生活用電費用為例，福州居民“一戶一表”用戶生活用電費用如表1：

本實踐活動引導學生搜集各自家庭的每月用電總量、高峰時段和低谷時段電量，通過計算得出自己家庭應選擇哪一種電價方式優惠，并推導出高峰時段電量和低谷時段電量之間達到什么樣的數量關系時，選擇執行峰谷分時電價.

教師在尊重學生意愿的基礎上合理分組，盡量每個小組后進生、中等生、優等生科學搭配，并指導學生制定合理可行的活動方案，引導學生合理分工，讓每個學生都為實踐活動承擔任務.

學生將整理搜集到的數據，按兩種繳費方式進行計算，并用表格和統計圖的方式呈現.各小組展示自己實踐活動的過程，分享在實踐活動中遇到的困難，以及如何解決的，分析結果，交流心得體會.教師引導學生進行總結和反思，引導學生發現不足，并指導如何改進，還要引導學生發現閃光點，鼓勵學生在今后的活動中揚長避短.

這類實踐活動型作業讓學生通過自己觀察、調查、同伴之間互相探索和交流完成，將課內所學應用于實際生活中，既開拓了學生的思路，又培養了學生的推理能力.

科學的單元作業設計改變了學生的學習方式，讓每位學生都能感受到良好的數學教育.數學閱讀材料讓學生對于數學的歷史和文化有了深入的了解；分層作業讓不同的學生有不同的發展、不同的收獲；跨學科作業適合現代科學技術與社會發展的需要；實踐活動作業打破了固有的作業形式，激發了學生學習數學的興趣，變被動學習為主動學習，養成了獨立思考的習慣、和同學合作交流的意識.整個過程與鐘啟泉教師提出的“單元設計一般遵循‘ADDIE模型”相吻合［2］，今后，教師們若能更加重視單元作業設計，那么每個學生都能在優化設計的作業中獲得自己的幸福體驗.

參考文獻：

［1］斯海霞，呂坤，張霞.初中數學單元作業設計特征分析及啟示——以20份單元作業設計為例［J］.中學數學月刊，2023（02）：51-54.

［2］鐘啟泉，學會單元設計［J］.新教育（科研版），2017（5）：1.

［責任編輯：李璟］

收稿日期：2022-12-15

作者簡介：劉燕（1969.6-），女，福建省南平人，本科，中學高級教師，從事中學數學教學研究；

連麗萍（1981.6-），女，福建省福州人，本科，中學一級教師，從事中學數學教學研究.

基金項目：本文為2021年度福州市教育信息技術研究立項課題《信息化環境下數學個性化作業設計》（課題編號FZDJ2021A27，主持人：劉燕）的研究成果之一.