數學建模教學：從問題提出到知識運用

鄭瑄

摘 要：杭州市阮洲奕老師上的一節題為“用吸管演奏樂曲”的數學課，開場生動，收尾升華，中間用環環相扣的問題鏈，一步一步地引導學生通過數據擬合建立吸管長度與所吹音調的函數模型，完成用吸管演奏奏樂曲的任務。由此得到關于數學建模教學的一些啟示：問題提出要真實自然、綜合開放，過程探究要從感性經驗上升到理性思考，知識運用要打破學科的界限。

關鍵詞：初中數學；數學建模；吸管奏樂；數據擬合；學科融合

近期，筆者參加了一個專題教研活動，聽了杭州市阮洲奕老師上的一節題為“用吸管演奏樂曲”的數學課。課上，阮老師引導學生通過數據擬合建立吸管長度與所吹音調的函數模型，完成用吸管演奏樂曲的任務。這節課使筆者受到了一些觸動，對數學建模教學的設計與實施有了更深的感悟。下面，先以欣賞的態度展現這節課的主要教學過程，再從教學啟示的角度談談筆者的感悟。

一、 教學過程欣賞

（一） 出人意表的開場

課始，大屏幕上出現五線譜，其上翻騰著各種音符。筆者和學生一樣滿懷好奇和期待，遐思翩躚：數學課怎么出現了樂譜？理性的數學與感性的音樂有什么關系？

“我們先來欣賞一段音樂。閉上眼睛，用心感受。”阮老師話音剛落，一股旋律流淌而出。如此，師生共同了進入一個音樂的磁場。

“好聽嗎？大家猜一猜：這段音樂是用什么樂器來演奏的呢？”學生猜測紛紜：笛子？排簫？卡祖笛？管風琴？……

“其實，這段音樂是用老師手中這根小小的吸管演奏的。”阮老師展示手中的吸管。學生驚嘆：哇哦！真沒想到！這是真的嗎？

緊接著，阮老師提出一個富有挑戰性的任務：“今天，我們就試著用吸管演奏樂曲。”

（二） 引人入勝的進程

挑戰性任務的提出出乎學生意料，那么，任務的完成如何引導學生入勝？阮老師通過環環相扣的問題鏈，一步一步地在學生的“最近發展區”搭建適切的學習支架，提供適當的解題線索，讓學生拾級而上，逐漸確定變量、設計實驗、收集數據、建立模型，從而利用數學知識解決音樂問題——特別是第四個問題，引導學生完成從定性到定量（從感性到理性）的飛躍。教學進程就在教師的發問、追問與學生的思考、實踐、討論、分享中逐漸展開——

師 （出示問題1）

吸管怎樣才能演奏音樂？

生 首先要能發出聲音，然后要能吹出不同的音調。

師 （出示問題2）

要吹出不同的音調，這又與哪些因素相關呢？

生 （眾說紛紜）

與空氣流速有關；與吸管的長度有關；與吸管的厚度有關；與吹氣的力度有關；與振動的頻率有關……

師 同學們的想法都很值得研究。今天，我們就先把問題聚焦到音調與吸管長度之間的關系上，看看長度改變了，音調到底會不會發生改變。（出示問題3）

改變吸管的長度，能吹出不同的音調嗎？有沒有同學愿意來試一試？

（兩位學生自告奮勇，上臺合作，一個剪、一個吹。大家發現：吸管剪得越短，吹出的音調越高。）

師 ?（出示問題4）

要想吹出中音la，應該使用長度為多少的吸管呢？

（學生陷入沉思之中。）

師 今天，我們就利用數學的方法來解決這個音樂的問題。不妨回想剛才的實踐嘗試——當吸管長度發生變化時，音調也隨之發生變化。在數學中，我們會聯想到什么知識呢？（出示問題5）

在數學中，我們如何研究兩個變量之間的關系？

生 （異口同聲）

利用函數。

師 對啊！長度和音調就是上述過程中的兩個變量，而函數正是數學中刻畫兩個變量之間對應關系的一種數學模型。（出示問題6）

用函數來研究，具體應怎么做？

生 先收集數據，再建立平面直角坐標系，畫出圖像，看看圖像長什么樣兒。

師 那么，要收集哪些數據呢？

生 要測量吸管的長度和用吸管吹出的音調。

生 在科學中，音調可以用振動頻率來表示，所以，測量音調就是測量振動頻率。

師 接下來，阮老師就帶領同學們一起收集數據。我們利用專業的聲學軟件（App）Phyphox測量振動頻率。取一根吸管，吹出穩定的波形時，軟件就會顯示出對應的振動頻率，這樣就可以得到相應的數據。

（師生合作收集實驗數據，結果如表1所示。）

師 觀察表中數據，大家有什么發現？

生 隨著吸管長度的增加，它的振動頻率逐漸降低，即它的音調慢慢變低。

師 為了更直觀地表示這組數據的變化規律，大家有什么方法？

生 可以在平面直角坐標系中描點，然后用光滑曲線連接，畫出圖像。

師 好，現在請同學們動手，在自己的學案紙上畫一畫這個函數的圖像。

（學生畫圖。）

師 觀察圖像，你認為可以用什么函數來刻畫這兩個變量之間的關系？

生 我認為它更接近于一個反比例函數。

師 其實，同學們畫的圖會存在一定的誤差。我們可以用現代科學技術更精準地擬合這個函數。請同學們在平板電腦上把所有的數據輸入老師提供的數據擬合軟件中。

（學生輸入數據后，軟件自動完成描點。師生先用一次函數模型試驗，發現很多點都不能落在一條直線上；再用反比例函數模型試驗，發現大多數點都落在一條反比例函數的曲線上。最后，計算機擬合出了這個反比例函數模型：f=86610/l。）

師 再回到剛才的問題4——要想吹出中音la，應該使用長度為多少的吸管呢？這個問題其實就變成已知反比例函數的某個函數值，求相應自變量值的簡單計算問題了。當然，先要利用“音調振動頻率表”查出中音la的振動頻率f=880Hz，從而可以算出吸管的長度l=984mm。（稍停）

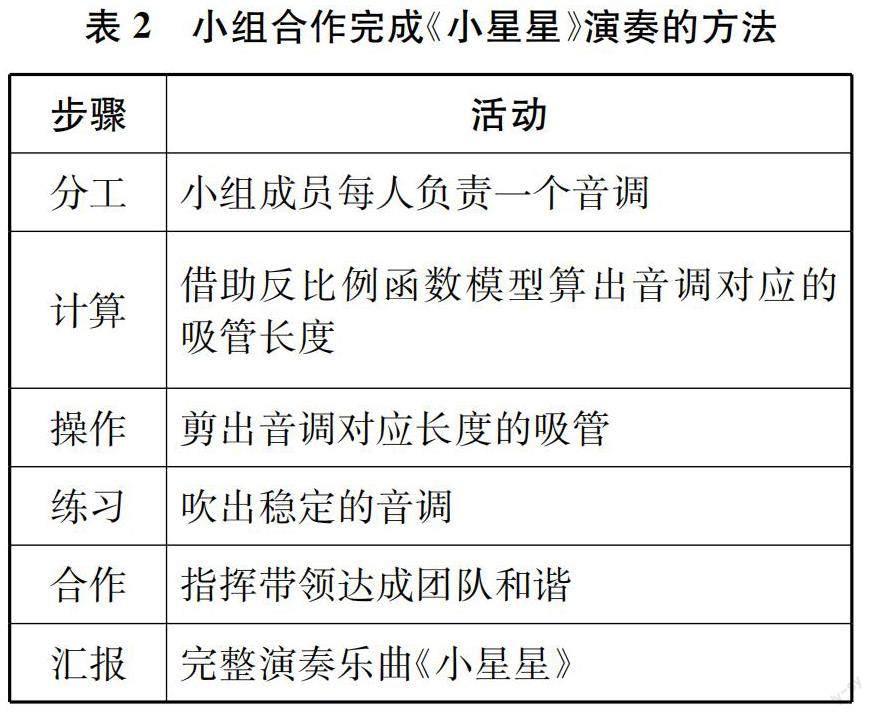
現在，阮老師要布置用吸管演奏樂曲的具體任務了——請各小組合作，根據樂譜吹奏莫扎特的樂曲《小星星》。（出示問題7）

七人小組要完成《小星星》的演奏，具體應該做？

（教師出示表2，提供完成任務的方法。各個小組開始活動，進入井然有序、忘我專注的狀態。）

師 這真的是阮老師聽過的最動人、最獨特的《小星星》了。

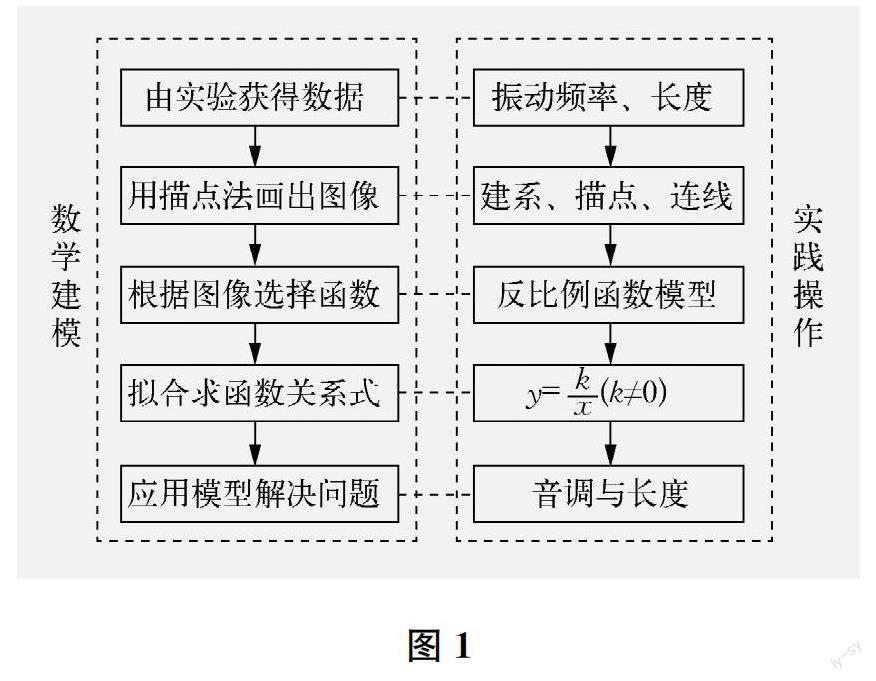
（教師引導學生回顧梳理整個數學建模的過程，得到圖1；體悟數學與音樂千絲萬縷的關系，得到下頁圖2。）

師 從古至今，數學與音樂一直是相輔相成的。2500年前，畢達哥拉斯第一次發現了音樂和數學的關系；中國古代通過數學運算研究音律；萊布尼茨認為音樂是一種隱藏的數學練習；傅立葉發現聲波是一種周期函數；而我們熟悉的音樂家貝多芬、肖邦、柴可夫斯基等，常用他們腦海中的曲線來譜曲。

（三）? 動人心弦的尾聲

這是一個令人動容的尾聲。素昧平生的師生，45分鐘的一節課，人生際遇中短短的緣聚，何為教育？筆者以為，衡量教育是否真正發生以及是否真正起到作用最真誠的標準，是看其有沒有激活和點燃學生的心靈，有沒有讓學生感知、感悟和感動。

師 同學們通過整節課的學習有什么感受和體會？

生 阮老師今天帶領我們經歷了一個完整的數學建模過程。我們平時都是先學函數，再到應用；而今天是先從生活中找音樂的應用，再回到數學中去找原理。真的很新穎、很神奇！

生 通過這節課，我知道數學還可以運用到生活中，可以與音樂相結合；感覺數學不只是紙上的運算，還是生活，有一種美麗的感受。

生 通過阮老師剛才舉出的那些古今中外名人軼事，我們知道，可以將數學運用在音樂中，也就是將數學運用于創造。阮老師這節課讓我感覺到數學學習的樂趣，使我更加熱愛生活，熱愛數學。

生 在這節課的學習過程中，我們為了研究數學與音樂的關系，用到了平板電腦等電子設備，還用了聲學軟件來測量聲音的振動頻率等。這使我感受到科技的力量，現代科學技術能夠有效幫助我們學習、研究。

生 這節課，我們一直在通過數學的美，彰顯音樂的韻律美。其實，我們還可以發散發聯想。比如，笛子、葫蘆絲都是通過開孔，運用氣流的振動來發出聲音的。所以，我們小組在討論的過程中，就從中汲取靈感，模仿其原理，在吸管上挖了很多的孔，制作了一種樂器。

（教師表揚了這個小組的創舉，也提出了意見：開孔太大，手捂不住。大家都快樂地笑出了聲。）

生 這節課教給我們，數學學習并不只是枯燥地掌握知識點，枯燥地“刷題”，單純地應付考試，更要將數學與生活結合。即教會了我們一種新的學習數學的方式，也讓我們體會到學習數學的樂趣。所以，非常感謝您！

生 這節課剛開始的時候，我完全想象不出數學與音樂究竟有什么關系，相信大多數同學也是一樣的感覺吧。但是，阮老師帶領我們一起探究，通過普通的吸管，讓音樂與數學進行了一個大大的碰撞。而且，小組同學之間討論得也很歡快，有一種在玩中學的感覺。然后，我還想問阮老師：數學源于生活，但也要回到生活，那么今天從吸管中學到的原理是否也可以用到其他東西上呢？

師 這個問題提得非常好！也就是說，我們能不能用今天學習的方法制作其他樂器？而且，改變樂器的載體后，剛才建立的反比例函數模型是否還適用？我們也許需要重新選擇函數模型，但是，其中蘊含的數學思想和研究方法是一脈相承的。實際上，這位同學也很好地說出了阮老師今天想給大家布置的作業——請每個小組運用不同的載體自制一個樂器，然后全班開一場不一樣的音樂會。到時候，記得發視頻給阮老師看哦。今天的課就上到這里。謝謝！

二、 教學啟示感悟

（一） 問題提出：真實自然、綜合開放

阮老師的課從本質上看，是帶領學生經歷了一次完整的數學建模過程。其實，初中數學教材中不乏要求學生進行數學建模的例子。比如，浙教版初中數學八年級上冊《5.5一次函數的簡單應用》的例1：

生物學家測得7條成熟的雄性鯨的全長y和吻尖到噴水孔的長度x的數據如表3所示。問：能否用一次函數刻畫x和y這兩個變量的關系？如果能，請求出這個一次函數的表達式。

同樣是讓學生經歷數學建模的過程，兩者的區別何在？筆者以為，教材舉的例子離學生的現實甚遠，而且數據的來源是提供式的，沒有讓學生理解測量這些數據的意義是什么。而阮老師課例中提出的問題貼近學生的現實，是真實自然的、有趣好玩的，富有吸引力，能夠培養學生提出問題的意識和能力；而且，是綜合開放的、結構不良的，充滿挑戰性，能讓學生經歷數學建模的全部過程。類似的例子還有“跑道上的數學問題”：何為400米標準半圓式跑道？如何畫出400米、800米分道跑的起跑線？……

數學建模的開端和關鍵是提出需要通過數學建模解決的有價值的問題。作為數學核心素養的表現，提出這樣的問題，需要在司空見慣的生活場景中、在錯綜復雜的學科情境中，用敏銳的數學眼光捕捉到有關的現象，轉化為相應的問題（任務）。其中蘊含著一系列心理活動：直覺——萌芽；關注——方向；醞釀——形成；理解——關系；提出——內心認定其有很好的生長趨勢。因此，教師不僅要具備這樣的意識和能力，而且要培養學生提出數學建模問題的意識和能力。

（二） 過程探究：從感性經驗上升到理性思考

中央電視臺《是真的嗎》欄目，曾經播出過一個關于吸管奏樂的節目。節目中，主持人向觀眾展示了一位網友提供的吸管長度數據，然后用按照如此長度制作的吸管吹出了音準很好的美妙音樂。這里展示的結果就是阮老師這節課帶領學生探究的問題。這個結果最初是怎么得到的呢？

當然，可以經過多次剪切、試音，從而非常接近音準，再將數據記錄下來。這種基于經驗的感性認知能夠帶來發現與創造，古往今來勞動人民用這樣的方法發現了大量知識，創造了大量財富。阮老師這節課也讓學生從感性認知出發展開探索：課始讓學生欣賞用吸管吹奏的樂曲，課中讓學生嘗試用吸管吹奏樂曲。

但若擁有數學素養，就可以用數學的眼光去觀察，用數學的思維去思考，用數學的語言去表達，從而進入理性研究的層面，高效地探尋精確的規律。正如阮老師這節課帶領學生做的：收集數據→借助技術→畫出圖像→計算機擬合→數學模型→回歸生活→解決問題。

總體而言，對好的數學建模問題的探索應該經歷一個從感性經驗上升到理性思考的過程。這也符合“大膽假設，小心求證”這一科學研究的一般范式。

（三） 知識運用：打破學科的界限

何珊云教授多次提到要“打破學科的界限”。她舉過這樣一個例子：你覺得“環游世界”會是一門什么課？大多數人的回答是“地理課”。而真實的學校課程（英國小學三年級）涉及11個學科，并以不同學科與環游世界的關聯作為學習內容和學習任務。

阮老師這節課亦然，不僅涉及數學和音樂，還涉及物理、材料、信息技術等學科。回顧阮老師這節課，其實學生在回答教師的問題時，呈現出了科學的思考——吸管奏樂可能與空氣流速有關、與振動頻率有關，只是阮老師沒有及時捕捉回應，抑或因為不在其預設中而忽略了。如果阮老師能對這些課堂生成給予適當的關注，引導學生課后展開自然而然的、能力所及的探究，那么這節課的教學價值將得到更充分的發揮。這也是我們在數學建模教學中應該特別注意的。

數學建模通常是基于問題和學習（problembased learning，簡稱PBL）或基于項目的學習（projectbased learning，也簡稱PBL）。其受到重視的根本原因就在于，我們生活的世界是一個復雜的世界，它是由無數問題、無數知識相互交織在一起的。其中的問題并不都是良構的，而常常是跨界的；知識是由問題引發的，其學科劃分常常是人為的；沒有跨界的“相輔”，就不易達成研究的“相成”。要培養學生的批判精神、創新意識、獨特思想，以適應當下與未來的現實，教育就要發生改變：讓學生不僅學習單一學科的知識，而且體驗更加真實而廣闊的世界。當然，這對教師的要求頗高，需要教師通過修煉從專才向通才轉型；對學生而言，也會在學習過程中感悟到學好數學以外其他學科的重要性。

進一步來看那些獲得偉大成就的人：阿基米德是古希臘偉大的哲學家、數學家、物理學家，還是百科式的科學家；弗朗西斯·培根是英國文藝復興時期的散文家、哲學家，也是實驗科學、近代歸納法的創始人；伯特蘭·羅素是英國著名的數學家、哲學家、邏輯學家、歷史學家，更是諾貝爾文學獎的獲得者……人為的學科劃分將世界割裂成若干個區域、若干個條塊，但是整個世界的整體聯系是真實存在的。學科的經緯愈分明，離教育的本質也愈偏遠。跨界無痕的學習，才是教育的本來面目。