課程思政視域下土木工程專業力學教學探析

曾廣尚

摘要：彈性力學是土木工程專業一門非常重要的課程，也是固體力學的一個重要分支。根據彈性力學的課程特點，文章從彈性力學與Schwartz交替法相結合處理多連通域孔洞問題以及類似案例解析等方面，探討教學方法，并在理論公式推導和應用分析過程中，深入挖掘相關知識點蘊含的課程思政元素，以期優化彈性力學基礎課與課程思政的協同育人效果。

關鍵詞：土木工程專業；彈性力學；Schwartz交替法；課程思政

彈性力學是力學、土木、機械、材料等理工科專業的基礎課程，它研究彈性物體在外力和其他外界因素作用下產生的變形與內力，也稱為彈性理論，是材料力學、結構力學、塑性力學和某些交叉學科的基礎。彈性力學課程的理論性強、概念抽象、公式復雜，且與數學理論聯系密切，是學生比較頭疼的課程。彈性力學課程中關于多連通域孔洞問題的理論在工程中應用非常廣泛，但在教學中比較難講透，是一個教學難點。因此，在學習過程中，學生會感到難以理解，在面對類似的力學問題時無從下手。筆者已經從事多年彈性力學研究，主要從幾個方面探討彈性力學結合Schwartz交替法求解多連通域力學問題的教學方法，并根據課程的特點，探索相關知識點的課程思政融合。

一、多連通域孔洞問題的處理方法——Schwartz交替法

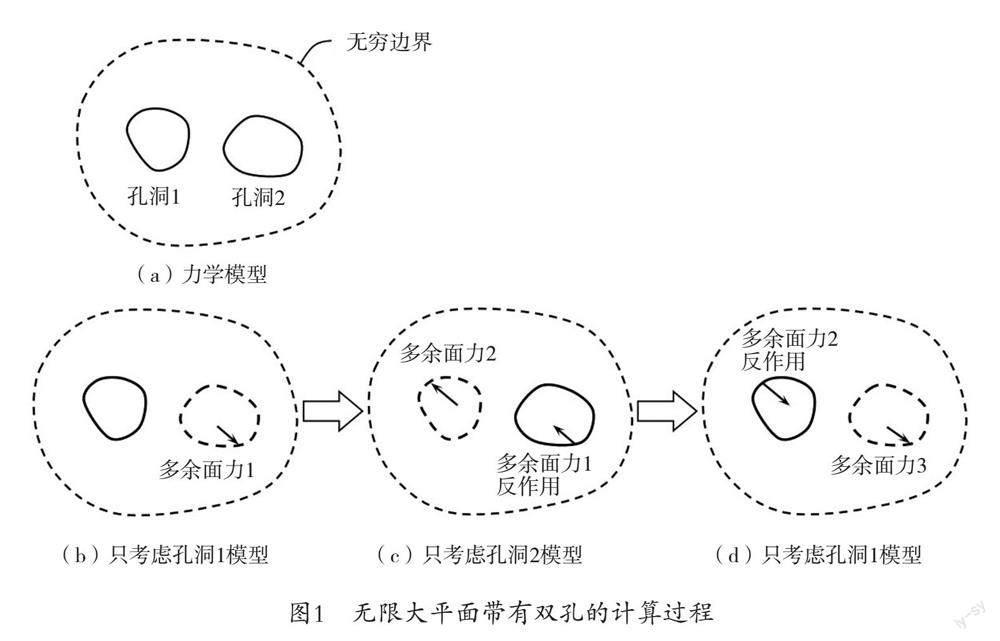
如圖1所示，為了加深學生對Schwartz交替法的理解，在教學中，教師可以將理論公式與更加直觀的模型圖相結合。

如圖1（a）所示，考慮一個無窮大的平面，里面包含兩個孔洞，即孔洞1和孔洞2，在無窮遠處有作用力的力學模型。由于這個力學模型存在兩個孔洞邊界，所以在數學上是一個雙連通域問題。對雙連通域問題，采用直接的求解方法來處理一般非常困難，甚至有些多連通域問題無法直接求解。為了使該復雜的力學問題變得更簡單，教師可以通過Schwartz交替法，把雙連通域問題拆分為兩個單連通域的問題分別處理，這兩個單連通域問題是分別考慮這兩個孔洞。具體的求解步驟如下。

第一步，只考慮孔洞1，如圖1（b）所示，是一個單孔問題。由于該力學模型只存在孔洞1一個邊界，所以這是一個單連通域問題。對單孔問題，教師可以利用彈性力學的方法求解出理論解答，接著根據理論解答可以求解出孔洞2虛擬邊界上的多余面力1。

第二步，只考慮孔洞2，將多余面力1反作用于孔洞2邊界上。如圖1（c）所示，該力學模型與圖1（b）的力學模型類似，也是一個單孔問題。由于該力學模型只存在孔洞2一個邊界，所以是一個單連通域問題。教師可以再利用彈性力學的方法求解出理論解答，接著根據理論解答求解出孔洞1虛擬邊界上的多余面力2。

第三步，只考慮孔洞1，將多余面力2反作用于孔洞1邊界上。如圖1（d）所示，該力學模型與圖1（b）的力學模型一樣，只是孔洞1邊界上的作用力與圖1（b）的不一樣，可以繼續利用彈性力學的方法求解出理論解答，接著根據理論解答求解出孔洞2虛擬邊界上的多余面力3。按照該方法一直交替迭代下去，兩個孔洞邊界上的多余面力會隨著迭代次數的增加而逐漸減小。當兩個孔洞邊界的多余面力足夠小時，即可停止迭代。

第四步，將每一步的計算結果疊加起來，即能得到無限大平面帶有雙孔力學響應的理論解答。這就是通過Schwartz交替法處理多連通域力學問題的基本思路。從數學上可以證明，按照該方法迭代下去得到的解答收斂于精確解。在實際計算中，Schwartz交替法的收斂速度是比較快的，其迭代次數可以根據工程問題的精度要求來確定，一般迭代幾步就可以得到很好的結果。

二、Schwartz交替法的案例解析

鑒于Schwartz交替法比較抽象難懂，并且在求解多孔應力集中問題還需要結合彈性力學知識，所以在講授過程中，教師需要結合具體的案例進行詳細分析：一方面，可以加深學生對彈性力學和Schwartz交替法的認識；另一方面，可以激發學生的學習興趣。在課堂教學中，筆者采用了以下方法。

第一，在介紹Schwartz交替法處理多連通域力學問題的原理之后，教師讓學生回顧曾經學過的結構力學中彎矩分配法的基本原理。例如，一般的連續梁結點角位移未知量的數目常有多個，彎矩分配法的基本原理也是每次計算時只考慮某一個結點角位移，其他結點角位移先用附加剛臂約束住，然后計算出其他結點由附加剛臂承受的不平衡力矩，接著依次單個釋放附加剛臂的約束，將不平衡力矩反作用，計算出其他結點由附加剛臂承受的不平衡力矩。按照該方法反復循環迭代下去，使各結點上的不平衡力矩逐漸減小，最后各結點的彎矩逐漸趨近于精確值。這可以讓學生在回顧結構力學知識的同時，更加透徹地理解Schwartz交替法。

第二，深埋雙孔隧道問題，只有兩個隧道邊界，也是一個雙連通域力學問題。教師可以運用Schwartz交替法結合彈性力學理論求解圍巖的應力和位移，即每次計算只考慮其中一個隧道，假定另一個隧道不存在，再通過彈性力學中的方法求解，然后反復交替迭代，使得兩個隧道邊界的多余面力足夠小，最后將每次的計算結果疊加起來所得到的最終解答趨近于精確解。

第三，淺埋單孔隧道問題，只有地表邊界和隧道邊界，也是一個雙連通域力學問題。教師可以運用Schwartz交替法結合彈性力學理論求解地層的應力和位移，即每次計算只考慮存在其中一個邊界問題（半平面不包含孔洞問題或者無窮大平面含有孔洞問題）。教師可以通過彈性力學中的方法來求解，然后反復交替迭代，使得兩個邊界的多余面力足夠小，最后將每次的計算結果疊加起來所得到的最終解答趨近于精確解。

第四，依此類推，運用Schwartz交替法結合彈性力學理論還可以解決更加復雜的力學問題，如半平面或無窮大平面含有任意個數孔洞的應力集中問題。因此，Schwartz交替法在處理多連通域力學問題時是非常便利的。

在講解完以上各案例之后，教師讓學生動手將每個案例的理論公式反復推導練習，學生對知識的理解會更加深刻。

三、彈性力學和Schwartz交替法教學中的課程思政

（一）愛國主義教育方面

彈性力學的理論知識非常重要，在課程思政教學過程中，教師可以通過展示實際工程案例，強調我國在土木工程方面不斷創新所取得的重大突破，培養學生的家國情懷與國際視野。例如，目前世界上最大的水利水電大壩——三峽大壩、世界上規模最大的跨海工程——港珠澳大橋、中國第一高樓——上海中心大廈、國家標志性建筑——國家體育場（鳥巢）等重要土建工程。教師通過典型的土木建筑工程案例，可以強化愛國主義教育，使學生充分了解我國在基礎建設方面取得的重大成就，并樹立專業報國的遠大理想。

（二）培養邏輯思維、發散思維和創新思維

彈性力學的公式非常多，推導比較復雜，是一門非常具有挑戰性的課程。Schwartz交替法原來是為了求解拉普拉斯方程的狄利克雷問題而提出的，該方法把雙連通域問題化為兩個單連通域問題進行處理。后來，有學者利用彈性力學結合Schwartz交替法有效地解決了多孔應力集中問題。如《圍巖力學分析中的解析方法》中通過彈性力學結合Schwartz交替法求解出了雙圓形孔洞問題的解答。在講解完雙圓形孔洞問題后，教師可以讓學生嘗試求解更加復雜的非圓形孔洞問題，以及多孔滲流問題，逐漸增加課程的難度。這樣的教學方式可以激發學生的求知欲，活躍課堂氣氛。學生在理論的推導訓練中，不僅提高了數學和力學思維交叉融合的能力，還提高了邏輯思維、發散思維和創新思維。

（三）培養化繁為簡，逐個突破問題的能力

Schwartz交替法是將多連通域問題化為一系列單連通域問題進行求解，也是一種逐次逼近的方法。換言之，Schwartz交替法是將一個復雜的問題拆分成一系列簡單的問題來處理，這種思想可以應用到學生的學習、生活中。在面臨復雜的問題時，一些學生會感到不知所措。其實，在很多情況下，學生可以將復雜的問題合理地轉化成若干個簡單的問題，將所有簡單的問題理清楚并解決好，這個復雜的問題也就迎刃而解了。因此，教師可以通過將Schwartz交替法原理與其他問題相聯系，引導學生抓住問題的本質，將問題化繁為簡。

（四）增強學生的專業責任意識、安全意識、行業標準規范意識

教師可以引入一些典型的工程事故案例，如2003年7月1日，正在建設中的上海軌道交通4號線某通道出現滲水引發坍塌，造成地面一幢建筑物發生傾斜，其裙房部分倒塌；2006 年1月22日，宜萬鐵路馬鹿菁隧道的平導洞在施工過程中發生特大突水事故；2010年7月11日，廣西賓陽縣那適2號隧道施工現場發生塌方事故。教師詳細講解相關工程事故案例發生的原因，讓學生充分了解這些工程事故發生的原因，增強學生的專業責任意識。

筆者以彈性力學結合Schwartz交替法求解多連通域問題的教學為例，結合啟發式教學法，引導學生在無窮大平面含有兩個孔的應力集中問題、半平面含有一個孔的應力集中問題的基礎上，思考半平面或無窮大平面含有任意個數孔洞的應力集中問題，從簡單的圓形孔洞問題拓展到復雜的非圓形孔洞問題。此外，筆者深入探索、挖掘與該教學內容相關的思政元素，并融入課堂教學，以思政元素開展德育工作，培養德才兼備的人才。

參考文獻：

[1]徐芝倫.彈性力學[M].北京：高等教育出版社，2016.

[2]朱慈勉，張偉平.結構力學[M].北京：高等教育出版社，2016.

[3]王學儉，石巖.新時代課程思政的內涵、特點、難點及應對策略[J].新疆師范大學學報（哲學社會科學版），2020（2）.

[4]陳子蔭.圍巖力學分析中的解析方法[M].北京：煤炭工業出版社，1994.

基金項目：上海市教委（人事處）高校青年教師培養資助計劃，項目編號：ZZSIT21023。

（作者單位：上海應用技術大學城市建設與安全工程學院）