初中方程中化歸思想的研究
許榮靜
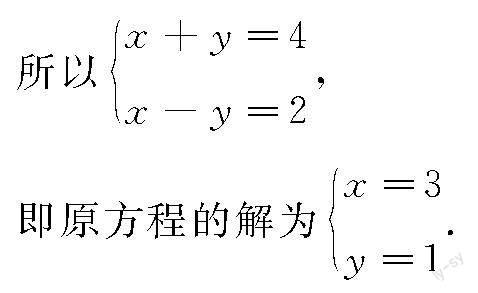


【摘要】化歸是轉化和歸結的簡稱,就是將問題化難為易、化繁為簡的過程.化歸思想作為最基礎的數學思想之一,是數學思想方法的精髓所在.化歸思想統籌著換元法、配方法等的運用,這些具體方法的產生都是以化未知為已知、化復雜為簡單為核心.將化歸應用于初中方程教學,對概念學習、方法掌握都有重大意義.
【關鍵詞】化歸思想;初中數學;解題教學
1 方程與代數式中的化歸思想
當x2+x+5的值為8時,求5x2+5x-2的值.
結論:5x2+5x-2=13.
分析:因為x2+x+5=8,
所以x2+x=3,
所以5x2+5x-2=5(x2+x)-2=13.
“式”是學習相應方程的前提.在求解方程的運算過程中,除了移項,其他的運算例如合并同類項、去括號、約分、添括號、通分等的知識都是包含在式的知識中學習的,因此方程求解可以轉化為將未知數移到等號另外一邊的“式”的運算.此題為化歸思想在概念性知識的應用.
2 一次方程(組)中的化歸思想
對于只含有兩個未知數的一次方程組,我們基本都可以利用去分母、去括號、消元進行求解,但是當將題目中數量關系變得更復雜時,再用去括號、通分、消元的方法就顯得很困難.此時考慮化歸思想,使用換元法去求解這類方程往往就可以變復雜為簡單.
結論:2a-2b=6.
則①+②可得2ax=4,
因為x=1,
所以2a=4,
由①②可得2by=2,
因為y=-1,
所以2b=-2,
所以2a-2b=4-(-2)=6.
此題利用加減消元進行轉化是最簡單且最快速的求解方法,此方法同樣也是化歸思想的一種具體體現.
3 分式方程中的化歸思想
因為x2-1>0,
所以x>1,
由原方程可知x>0,
所以y>0,
所以由②的平方可得x2+y2+2xy=8……③,
將①帶入③中,即(xy)2+2xy=8,
所以xy=2或者xy=-4<0(舍去),
若按照常規的解法,將方程先進行去分母、去括號、去根號等一系列操作,計算量大且初中階段很難完成求解.如果本著化歸的思想,就很容易想到可以利用換元法,在換元后的解題過程中,將分式方程轉化為二元方程組.雖然增加了變量,但方程組的求解過程會顯得更容易,關系也會更清晰.這也體現出化歸的應用并非是固定的,而是向著可能解決問題的方向歸結,隨機應變的.
4 一元二次方程中的化歸思想
分析:因為x2+4x-5=0,
所以x2+4x=5,
所以x2+4x+4=5+4,即(x+2)2=32,
在求解一元二次方程或者可化為一元二次方程的有關方程時,不論是使用配方法、公式法還是因式分解法,都是以化歸思想“化二次為一次”為指導的.不僅如此,通過體驗多次化歸的過程,學生自己就可以歸納總結出解代數方程的一些基本思路,即將高次方程化為低次方程、將無理方程化為有理方程,將分式方程化為整式方程.
5 結語
將化歸思想應用于方程思想教學中,促使學生意識到化歸在思維活動中的重要作用,通過不斷引導學生對方程概念學習與解題過程做出反思,讓學生明確方程應用題類型的劃分是基于化歸思想指導下的模型構建.最終在滲透和明確化歸思想相結合的過程中,不斷引導學生將學習化歸、掌握化歸、運用化歸三者結合起來.
本研究圍繞著化歸思想的含義,挖掘化歸思想在數學方程知識中的應用,將隱晦的化歸思想具現化,促使學生在教師富含化歸應用的教學活動中不斷學習化歸思想.將化歸應用于初中方程教學的這一過程,也是將化歸思想傳授給學生的過程,不斷研究化歸思想教學的方法,希望能夠切實為提升數學思想提供實踐參考.
參考文獻:
[1]楊海艷.淺談化歸思想在初中數學教學中的滲透[J].教學管理與教育研究,2022,7(19):6-7.
[2]潘成好.化歸思想在初中數學教學中的應用研究[J].讀寫算,2020(16):120.
[3]陳衛麗.例說解方程中的化歸轉化思想[J].初中數學教與學,2021(17):37-38+4.
[4]倪玨.七年級數學教學化歸思想的應用滲透[J].文理導航(中旬),2020(05):12+15.

