分類討論思想解初中數學問題的不同情形應用分析
張濤
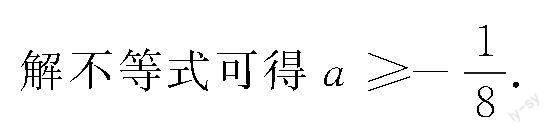
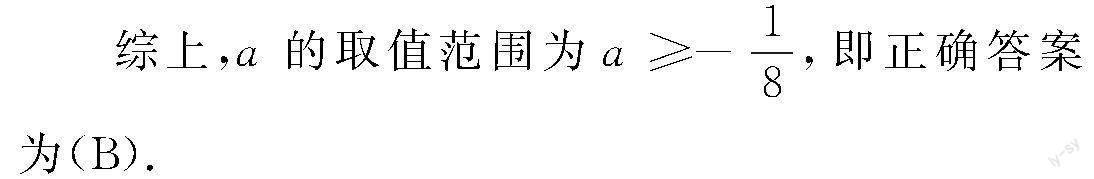
【摘要】分類討論思想是指在一些不確定的條件下,不能用統一的思路或結論解答問題時,按照可能出現的情況分別進行討論并解答問題的一種方法,也是解答初中數學問題的常見方法之一.本文主要對三角形問題、動點問題、方程問題的分類討論具體應用進行具體分析,結合具體例題總結分類討論思想的應用情形,以此幫助學生獲得更高的分數,更全面地思考問題.
【關鍵詞】初中數學;分類思想;解題研究
1 三角形問題分類討論
三角形的邊長和角度是考查的熱門角度,問題通常不會給出具體的三角形圖形,一些模棱兩可的條件導致多種三角形存在,直接解答有可能出現漏解和誤解的情況.對三角形問題分類討論,首先根據已知條件判斷三角形形狀是否明確,若不確定則需要分類討論,其次一些具有明確特征的三角形也需要分類討論,如直角三角形未說明直角邊和斜邊需要分類,等腰三角形未說明明確的腰和底也同樣需要分類討論.分類討論解題過程中,要注意三角形的分類準確不重復,才能正確解答問題.
例1 在△ABC中,∠B=25°,AD是BC邊上的高,并且AD2=BD·DC,則∠BCA的度數為.
剖析 該問題沒有說明△ABC的具體形狀,故高AD有兩種情況,分別在三角形內部和三角形外部,畫出兩種情況對應的圖形,結合已知條件和相似三角形分析,即可得知問題所求角度.
解
①如圖1,當三角形的高AD位于△ABC內部時,
由AD2=BD·DC可得△ABD∽△CAD,
因為∠B+∠BAD=90°,∠B=∠CAD,
所以∠CAD+∠BAD=∠BAC=90°,即△ABC為直角三角形,
因為∠B=25°,
所以∠BCA=90°-∠B=65°.
②如圖2,當三角形的高AD位于△ABC外部時,
由AD2=BD·DC可得△ABD∽△CAD,
因為∠B=∠CAD=25°,
所以∠BCA=∠CAD+∠ADC=25°+90°=115°.
綜上,∠BCA的度數為65°或115°.
2 動點問題分類討論
初中數學中動點問題通常以幾何圖形作為問題背景,當動點運動到不同位置時對應的情況也有所不同,故需要分類討論來解答問題.運用分類討論解答動點問題時,首先應根據動點所在的不同位置進行分類,如動點位于幾何圖形的不同邊長進行分類,其次在不同情況下分析問題涉及的函數關系,最后對所有情況進行綜合從而得出答案.動點問題常常會涉及函數關系,故熟練掌握函數類型和解析式求解有助于更高效地解答這類問題.
例2 如圖3,正方形ABCD的邊長為3cm,動點M從點B出發以3cm/s的速度沿BC-CD-DA運動,到達點A停止運動,另一動點N同時從B點出發,以1cm/s的速度沿BA向點A運動,到達點A停止運動,設點M的運動時間為xs,△AMN的面積為ycm2,則y關于x的函數圖象是(? )
剖析 動點M與動點N都在運動,但點N運動不改變邊長位置,故解題時應根據點M處于不同線段進行分類討論,分別有點M在BC上、在CD上、在AD上三種不同情況,結合三角形面積公式表示y和x的關系得到函數表達式,即可對圖象進行判斷和排除,最終符合所有情況的圖形即為正確答案.
解析 由題意可得BN=x,
①當0≤x≤1時,點M在BC上,
BM=3x,AN=3-x,
故(C)錯誤;
②當1≤x≤2時,點M在CD上,
故(D)錯誤;
③當2≤x≤3時,點M在AD上,
AM=9-3x,
故(B)錯誤.
綜上,正確答案為(A).
3 方程問題分類討論
與方程有關的初中數學問題也同樣是考查的熱門題型,涉及的方程類型有一元一次、一元二次、二元一次方程,問題常常會因為存在不確定范圍的參數導致方程類型不明確,需要運用分類討論方法解題.分類討論可以對方程的類型做出討論,也可以對一元二次函數的實數根個數進行討論,解答方程類問題,需要熟記一些方程的概念和實數根之間的關系表達式,結合分類討論方法靈活運用這些知識點即可解答問題.
例3 關于x的方程a-1x2+3x-2=0有實數根,則a的取值范圍為(? )
剖析 由于方程的最高次項系數是a-1,a-1=0和a-1≠0分別對應兩種不同類型的方程,分情況討論一元一次方程和一元二次方程有實數根時對應的參數a的取值范圍,即可求出正確的答案.
解析 ①當a-1≠0時,即a≠1,
由題意可得Δ=32-4a-1×-2≥0,
②當a-1=0時,即a=1,
可知一元一次方程3x-2=0有實數根,
故a=1成立.
4 結語
在解答一些數學問題時,常常會因為沒有明確的定義或范圍導致多種情況的出現,分類討論思想的靈活運用是解答這些問題的關鍵.在三角形問題中,通常根據邊長、角度兩個角度進行分類,討論不同三角形的具體情況;在動點問題中,常常根據動點所處的不同位置進行分類,討論不同位置對應的函數關系;在方程問題中,主要根據方程類型、實數根個數進行分類,討論對應的情況.在這些題型中應用分類討論思想,有助于提高學生的解題效率,也能幫助學生更全面地分析問題,解決問題.

