聚焦內容探索主線，實踐探究教學感悟

劉勤鳳

［摘? 要］ “三角形的中位線”這節內容對學生的知識儲備和思想水平要求較高，整個內容圍繞概念、性質、定理展開，具有一定的層次性和邏輯性. 教學過程中，教師要把握教學核心，提取主線，精設探究環節，引導學生進行實踐探究. 文章深入分析教學內容，開展教學探討，并進行思考感悟.

［關鍵詞］ 三角形中位線；教學探索；教學感悟

“三角形的中位線”是蘇科版義務教育教科書八年級下冊第九章的重要教學內容，中位線的概念教學和性質定理是教學的關鍵. 教學中教師應當充分調動學生參與活動，讓學生經歷探究過程，獲得知識的自然生長.

關于教學內容的分析

教材將“三角形的中位線”內容安排在“平行四邊形的性質和判定”之后，此時學生已經掌握了三角形的性質以及全等三角形的相關知識，故教學內容可視為平行四邊形研究的延伸. 實際教學時，教師可以利用平行四邊形的知識內容輔助探究.

“三角形的中位線”這一內容的教學核心是中位線的概念和性質定理，無論是概念還是性質定理，對于學生來說均較為陌生. 教學時，教師要把握學情，遵循學生的認知規律，采用實踐發現、自主思考、實驗探究的導學模式，圍繞“中位線”開展概念認識、性質定理探究. 教師設計豐富的活動，能讓學生經歷數學抽象轉化的探索過程，能讓學生體驗發現問題、解決問題的過程.

基于上述內容及目標分析，實際教學時筆者建議采用如下探究方式：

（1）折紙實踐，發現中位線；

（2）拼接實驗，感知中位線的性質；

（3）思維推理，探索中位線的性質定理；

（4）靈活運用，探究性質定理的應用策略.

關于教學的實踐探討

根據上述章節內容分析及教學編排，實際教學時教師可按照“發現中位線→感知中位線的性質→探究性質定理→定理應用探究”這一主線，合理設計教學活動，讓學生參與教學過程，掌握知識，提升能力.

1. 趣味折紙，發現中位線

當下的課堂教學倡導以“動”啟智，由“變”探學，即營造豐富、生動的課堂，讓學生在活動中發現知識、探索知識. 對于三角形中位線的探索，教師教學時可結合折紙活動，引導學生動手實踐，自主探究.

折紙活動：利用直角三角形折出中位線

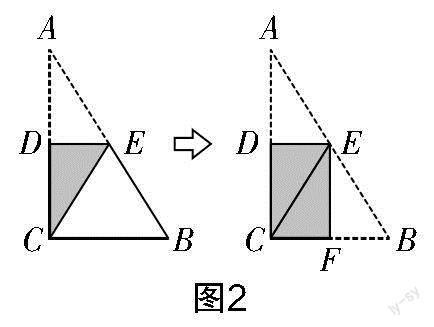
（1）請學生預先準備直角三角形，將三角形按照圖1所示的方式折疊，使得點A和點C重合，觀察折痕，看有什么發現.

（2）嘗試按照圖2所示的方式再次折疊，看看又有什么發現.

讓學生參與折紙，能激發學生的興趣. 學生完成折紙操作后，需要教師引導學生關注折痕與直角三角形一邊的位置關系，以及折痕的兩個端點的位置特點. 學生的思維能力存在差異，教學中教師可以讓學生進行小組討論，共享觀點，從而發現折紙活動中DE，EF分別與邊BC，AC的數量關系和位置關系.

接下來教師適時給出三角形中位線的定義，關注定義中“兩邊中點”這一關鍵詞，引導學生思考“同一三角形中可作幾條中位線”，并從直角三角形拓展到一般三角形，讓學生全面認識三角形的中位線.

2. 拼接活動，感知性質

中位線的性質是探究的重點，完成概念教學后，教師同樣可以設計剪紙活動，引導學生進行折紙拼接，直觀感知中位線的性質.

剪紙活動：拼接發現性質.

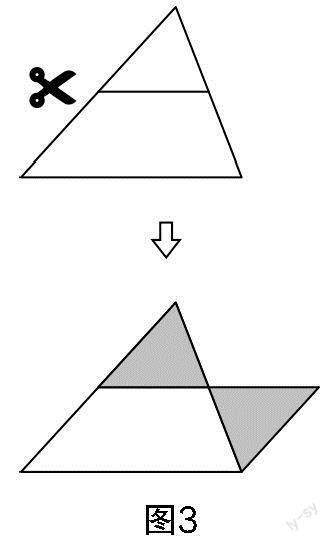
師：請同學們準備一個三角形，畫出任意一條中位線，然后沿著中位線將三角形剪成兩部分.

思考：如何拼接可將兩部分拼成一個平行四邊形？

設問：觀察拼成的四邊形，可以得到哪些結論？

本環節的實踐操作性較強，需要學生操作與思考相結合. 拼接四邊形有兩種策略，以上述圖3的方案為例. 教學中教師要引導學生把握拼接過程中三角形旋轉的特性，從與第三邊的數量和位置兩大關系入手進行思考.

教師引導時可由拼接圖建立幾何模型，如圖4所示，并設置如下問題.

問題1：△CGF和△BEF是什么關系？可以得出怎樣的結論？

問題2：分組測量GF和EF、GE和AB的長度，可以得出四邊形GABE有什么特點？

問題3：可知GF+FE=GE，從中可以得出怎樣的結論？

問題4：請從數量和位置兩方面來總結GF與AB之間的關系.

教學中教師要引導學生利用幾何語言和文字語言來進行性質定理的概括. 而采用拼接實踐和引導思考的方式，能夠讓學生在活動中發現三角形中位線的性質. 活動化靜為動、動靜結合，既注重知識的整體性構建，又可激發學生的求知欲. 同時，操作實踐過程可深化學生理解知識，活動中學生可感受轉化思想，掌握幾何探究的方法.

3. 思維推理，定理證明

通過實踐操作，學生對三角形中位線的性質有了初步的了解. 但定理的證明建議采用思維推理的方式，即從幾何視角，引導學生利用所學知識進行推理證明. 定理的證明方式有很多，可從補圖和幾何旋轉兩大視角來進行.

【證明探究1：補圖證明】

證明思路：補充圖形→構建全等三角形→提取平行四邊形→推導幾何結論

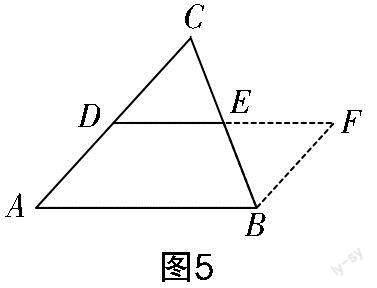
具體過程如下：如圖5所示，已知DE為△ABC的中位線，延長DE至點F，使得EF=DE，連接BF.

全等證明——DE=EF，∠CED=∠BEF，CE=BE，則有△CED≌△BEF，從而有CD=BF，∠CDE=∠EFB，可證AD∥BF.

平行四邊形提取——已知AD∥BF，BF=CD=AD，所以四邊形ADFB為平行四邊形.

結論推導——由于四邊形ADFB為平行四邊形，所以AB=DF=2DE，DE∥AB.

【證明探究2：旋轉證明】

該證明依托幾何旋轉特性，參照的是折紙拼接的思路. 如以活動中的圖形（圖4）為例，思路過程為：旋轉△CGF→共線證明→提取平行四邊形→推導幾何結論.

具體過程如下：已知GF為△ABC的中位線，如圖6所示，將△CGF繞點F順時針旋轉180°，使得點C旋轉到點B的位置，得到△BEF.

幾何旋轉——根據旋轉特性可知△CGF≌△BEF，于是可推知∠GFC=∠BFE，GF=FE，CG=BE.

共線證明——因為∠GFC+∠GFB=180°，∠GFC=∠BFE，所以∠GFB+∠BFE=180°. 所以G，F，E三點共線.

平行四邊形提取——已知∠CGF=∠FEB，所以CG∥BE，即AG∥BE. 又知BE=CG=AG，所以四邊形GABE為平行四邊形.

結論推導——由于四邊形GABE為平行四邊形，所以AB=GE=2GF，AB∥GF.

上述采用的補圖和旋轉證明方法，均以平行四邊形的性質為紐帶，注重思維推理的過程. 這種教學方式立足學生的知識水平，注重知識之間的相互聯系，構建了圖形探索的多種證法及途徑，有利于發散學生的思維.

4. 定理的應用探究

中位線的性質定理在幾何中有著廣泛的應用，教學中教師要引導學生關注定理的數量關系和位置關系兩部分內容，應用探究時可從解決實際問題和求解幾何綜合題兩大視角來進行.

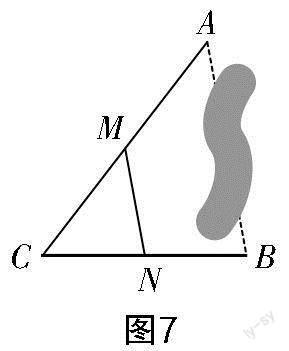
實際應用：如圖7所示，A，B兩點被池塘隔開，在AB外選一點C，連接AC和BC，這樣便可求出A，B兩點間的實際距離，你知道這根據的是什么原理嗎？

教學引導：教師引導學生參考中位線的知識，在AC和BC邊上各取中點M和N，然后利用中位線的性質得出AB=2MN，再通過測量MN的距離推導出AB的距離.

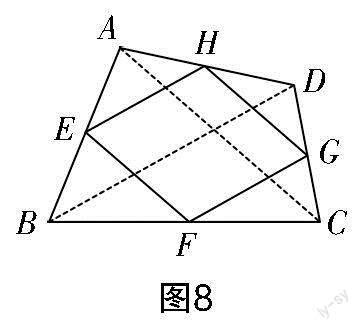
綜合應用：如圖8所示，E，F，G，H四點分別是四邊形ABCD四條邊的中點，猜想四邊形EFGH的形狀并證明.

教學引導：教師引導學生連接AC和BD，分別證明EH，FG，HG，EF分別為對應三角形的中位線，再利用中位線的性質得到EH∥BD∥FG，HG∥AC∥EF，從而證明四邊形EFGH為平行四邊形.

關于教學的思考與感悟

1. 把握教學重點，規劃設計主線

教材在安排“三角形的中位線”內容時具有針對性，是對平行四邊形相關知識的延伸. 教學時教師要充分定位中位線，把握教學重點，基于教學核心，規劃教學主線. 教師要基于教學主線來重構教材，引導學生感知中位線、探索中位線性質、論證性質定理，最終達到靈活運用的目的. 所以教師在分析教材內容時要深刻、全面，核心突出，主線鮮明.

2. 活動引導探究，知識自然生成

該內容涵蓋了概念和性質定理，探究性極強，對學生而言理解上具有一定的難度，但采用活動探究的方式就可以讓知識定理自然生成，并提升學生的探究能力. 活動設計需要兼顧操作實踐與問題引導，要讓學生參與活動，通過自主觀察、操作感知新知，教師則在各環節合理設計引導性問題，調動學生的思維，讓學生提出猜想、分析推理、獲得結論.

3. 合情推理演繹，注重思維培養

知識探究過程中的思維引導既是教學的關鍵，又是知識升華的重要方式，尤其是性質定理教學中，教師要引導學生合情推理，發現問題并提出猜想，掌握相應的探究方法. 教學中教師要融合思想方法，將歸納、類比、特殊化、一般化等思想方法融入教學中，關注學生的思維活動，給學生留足思考空間，使學生積累探究經驗的同時獲得思維的提升.