吃透基本圖形對提升學生數學學力的研究

楊麗萍

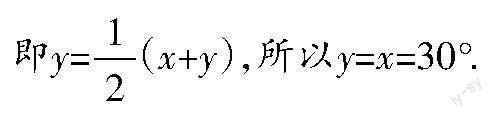
［摘? 要］ 平面幾何中的基本圖形是指幾何問題中常見的、具有典型特征，能夠得到常用結論的一些圖形. 基本圖形的掌握，有助于提高學生的幾何直觀和想象能力，再通過猜測、驗證、發現結論，能從某種程度上有效促進學生幾何思維的發展.

［關鍵詞］ 基本圖形；數學教學；數學學力.

《義務教育數學課程標準（2022年版）》指出，數學源于對現實世界的抽象，我們在學數學的過程中，可以通過對數量和數量關系、圖形和圖形關系的抽象、提煉，得到新的研究對象具備的結論或關系. 教師的教育教學應注重對基礎知識、基本技能的教學，并督促學生理解基礎知識、掌握基本技能. 掌握“知識與技能”是學生發展的最基礎目標，同時要落實“數學思考”“問題解決”“情感態度”等目標. 在教學中，教師應注重學生對所學知識的理解與掌握，讓學生體會數學知識之間的關聯，實現數學知識真正意義上的內化. 當然，學生掌握數學知識，絕對不能依賴死記硬背，而應在理解的基礎上應用知識，并不斷鞏固、深化、內化知識. 筆者認為，根據課程標準的指導意見，教師在教學中，應注重培養學生的數學學力，使學生進一步領悟數學核心素養（數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析）. 數學學力與數學核心素養之間并不是相互獨立的，二者相輔相成. 數學核心素養對數學教學具有明確的指導意義，起著統領性的作用. 數學學力則可以看作是在核心素養指導下數學學習中較為實用的具體操作方法，它是數學核心素養的現實操作路徑，具有可操作性、具體化的特點.

學生都想學好數學這門課，但無奈自身數學學力的缺乏，使得絕大部分學生學得非常吃力. 筆者也經常聽到身邊的同事這樣吐槽：“這道題我都講了無數遍了，怎么還有這么多人做不對？”從這句話中可以得到兩個信息：一，這道題經常考，在平時的練習中出現的頻次較高，姑且說它是典型題；二，學生的學習效率不高，一個高頻出現的練習題，學生多次接觸后仍有部分做不對. 基于這兩點，筆者深刻地體會到，在平時的教學中教師應采取措施去提升、發展學生的數學學力. 數學家波利亞曾經主張：與其做大量的難題，不如把一道題的各個側面研究通透，這樣會積累更好的經驗，提高解決其他問題的能力. 基于波利亞的主張，教師在教學中應深挖問題本源. 平面幾何問題的本源是一些基本圖形，具體指幾何問題中常見的、具有典型特征，能夠得到常用結論的一些圖形. 基于某一類基本圖形的變式題或拓展題比比皆是，學生只要熟練掌握基本圖形，經歷猜測、驗證、發現結論的過程，便能求解. 在求解的過程中，學生提高了幾何直觀和想象能力，發展了數學思維，對提升數學學力起到了立竿見影的效果. 下面以基本圖形“飛鏢形”在解題中的靈活應用為例，進行具體闡述.

基本圖形——“飛鏢形”

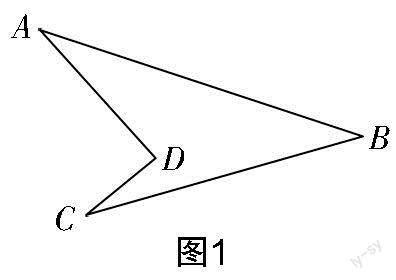
如圖1所示的凹四邊形稱為“飛鏢形”，在“飛鏢形”圖形中，∠ADC與∠A，∠C，∠B之間的數量關系為∠ADC=∠A+∠C+∠B. 該數量關系可以通過添加輔助線（連接BD并延長），并利用三角形的外角性質得到.

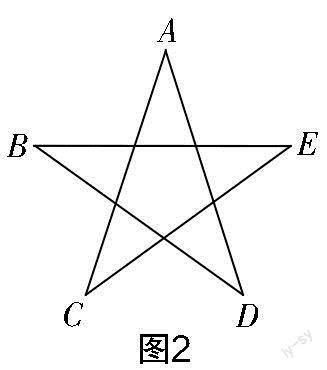
試題1? 一個五角星如圖2所示，則∠A+∠B+∠C+∠D+∠E=_____.

對于此題，有些學生無從下手，但是仔細觀察圖形，不難發現該圖形中含有基本圖形“飛鏢形”，利用“飛鏢形”的重要結論，再結合三角形的外角性質，很容易得到該題的答案為180°.

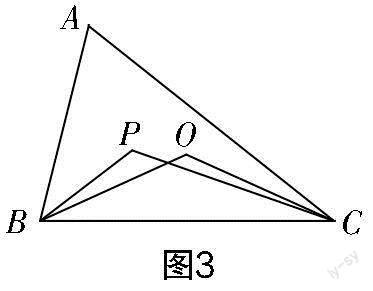
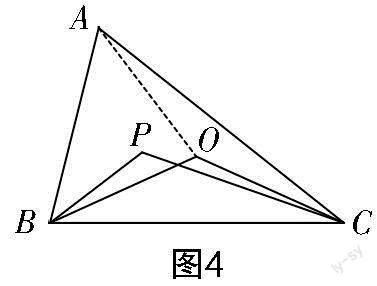
試題2? 如圖3所示，P是△ABC三個內角平分線的交點，O是△ABC三邊垂直平分線的交點. 若∠BPC=115°，則∠BOC=______.

∠OCA+∠BAC=∠OAB+∠OAC+∠BAC=∠BAC+∠BAC=2∠BAC=100°.

以上兩題的解決，說明了在復雜圖形中提煉出基本圖形的重要性. 所以教師在教學中一定要引導和幫助學生提煉出基本圖形，并要求學生記住基本圖形相應的結論.

變式1? 在四邊形ABCD中，∠A=x，∠C=y.

（1）∠ABC+∠ADC=______（用含有x，y的代數式表示）.

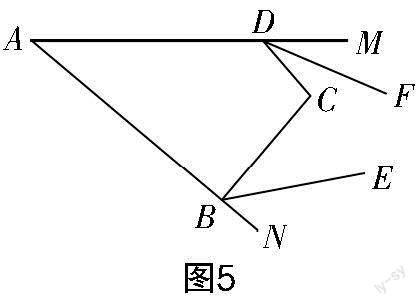
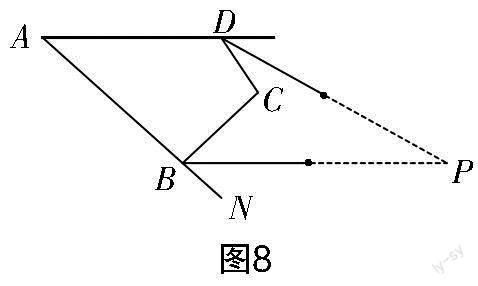
（2）如圖5所示，BE，DF分別為∠ABC的外角平分線和∠ADC的外角平分線.

①若BE∥DF，x=30°，則y=______；

②當y=2x時，若BE與DF交于點P，且∠DPB=20°，求y的值.

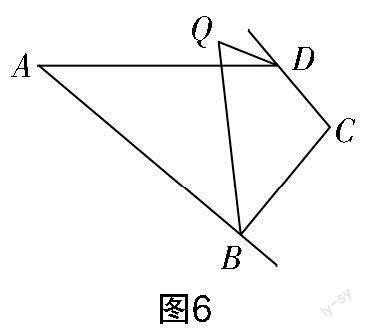
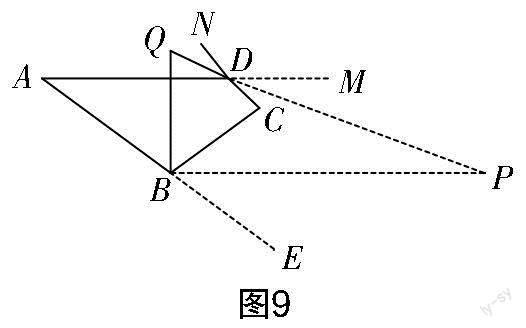
（3）如圖6所示，∠ABC的平分線與∠ADC的外角平分線交于點Q，則∠Q=______（用含有x，y的代數式表示）.

第（1）題比較簡單，利用四邊形的內角和為360°就可以得到∠ABC+∠ADC=360°-x-y.

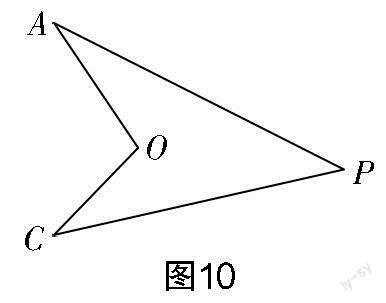
變式2? 我們將圖10所示的凹四邊形稱為“飛鏢形”. 在“飛鏢形”中，我們很容易得到∠AOC與∠A，∠C，∠P存在數量關系∠AOC=∠A+∠C+∠P.

利用“飛鏢形”模型解決下列問題：

（1）如圖11所示，若AP平分∠BAD，CP平分∠BCD，∠B=28°，∠D=48°，求∠P的大小；

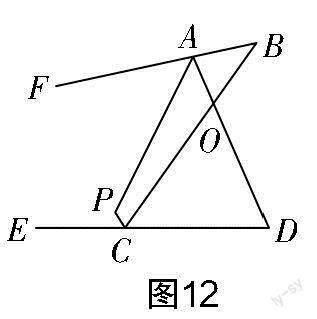
（2）如圖12所示，已知直線AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P與∠B，∠D的關系，并說明理由；

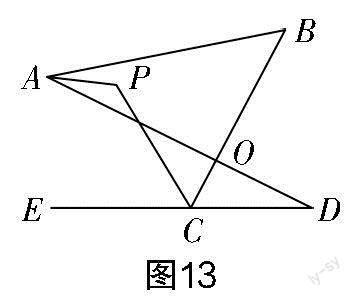
（3）如圖13所示，已知直線AP平分∠BAD，CP平分∠BCD的外角∠BCE，則∠P與∠B，∠D的關系為______.

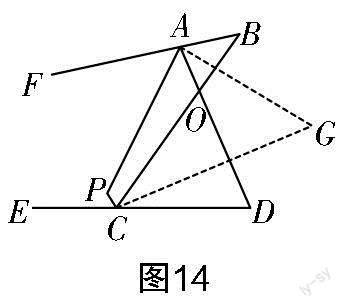
對于第（3）題，有了第（2）題的解題經驗，該題不難想到輔助線：作∠DCO的平分線交AP的延長線于點G（如圖15所示）. 圖15中仍含有兩個

解后反思

上面2道變式題都是測試中的壓軸題，在學生看來，無疑難度非常大. 一部分有畏難情緒的學生，光看題目中復雜的圖形就望而卻步了. 而我們在解決上面兩道“難題”時 ，能從復雜圖形中找到熟悉的基本圖形──“飛鏢形”，在難度層層遞進的梯度問題解決中，運用了類比、追本溯源的方法，從而輕松、靈活地解決了“難題”.? 以研究平面圖形為主的初中幾何，隨著所學知識的增多、內容的加深，一些幾何題的綜合性和復雜性也不斷增加，學生在解題過程中需要養成良好的數學圖形觀察習慣，要將復雜圖形轉化或者類比為常見的基本圖形. 在教學中，對于復雜題型、圖形，教師要善于引導學生進行去復雜化，轉化、提煉出基本圖形或轉化成熟悉的知識去解決. 長此以往地訓練，必然有利于學生數學學力的培養與提升. “基本圖形”只是初中數學幾何中的一小部分，通過吃透“基本圖形”來提升數學學力的措施也啟發我們，可以從與學生聯系比較密切的典型題型出發，通過學生對于典型題型的理解與吃透來讓學生積累解題經驗，形成“模式”. 這樣，在學生面對稍難或一些變式題型時，就可以透過現象看本質，通過類比，洞察解題規律與本質，從而在解題時達到事半功倍的效果.