基于“概念圖” 的初中數學教學設計與思考

摘要：文中結合展示課“圓的對稱性”（第1課時）給出了教學設計實踐過程及其思考，借助“概念圖”圍繞教材、學生、教法三方面開展教學設計.同時，給出了自己的經驗總結：使用概念圖開展教學設計，整體把握教學設計；充分考慮學生學情；創“模型圖”助力“三會”；設問題串，遷移經驗.

關鍵詞：概念圖；教學設計；學情；模型圖；問題串

近日，筆者應邀赴外地參加同課異構課堂教學活動，課題是“圓的對稱性”第1課時.拿到課題后，筆者先鉆研教材，吃透教材，進而了解學情，研究教法.本人多年來對使用“概念圖”組織教學進行了大量的實踐探索，本節課也可以使用“概念圖”開展教學.

“概念圖”是由約瑟夫·D·諾瓦克提出的，是一種知識以及知識之間的關系的網絡圖形化表征，也是思維可視化的表征.一幅概念圖一般由“節點”“鏈接”和“有關文字標注”組成.“概念圖”作為教學設計的工具，有利于教師從一堂課的整體角度入手備課，幫助教師整體把握知識框架和教學思路，增強教師的教學技能.

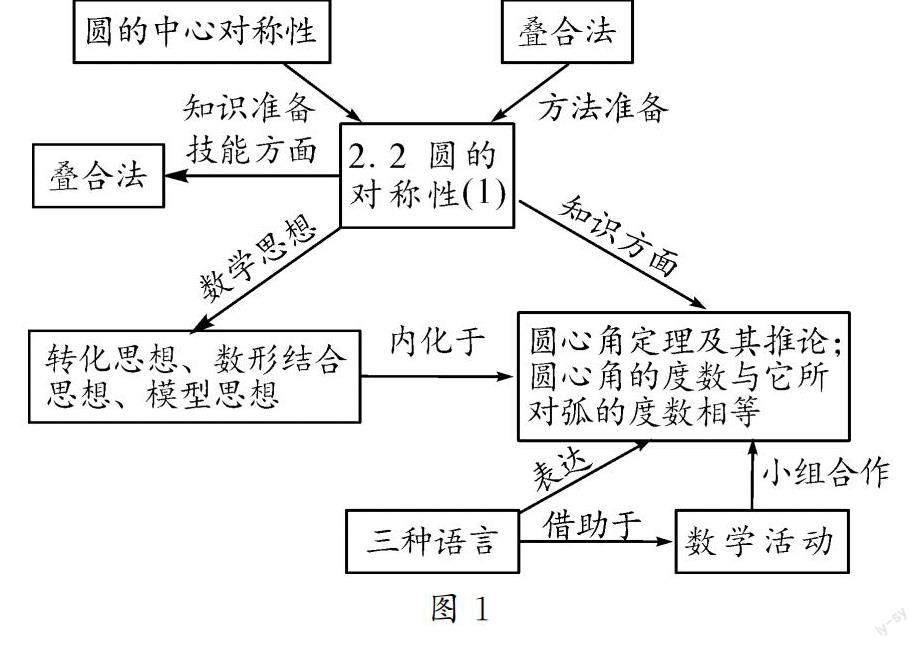
圍繞怎樣才能上好這節課進行教學設計，筆者先找到了相關“節點”：圓心角定理及其推論，疊合法，轉化思想、數形結合思想、模型思想，三種語言，等等.相關的“標注”：知識準備、方法準備、知識方面、技能方面、數學思想等.用箭頭“鏈接”各“節點”.緊接著，設計了一個本節課的鏈式概念圖^［1］（如圖1）.

下面從教材研究、“學生”研究、教法研究三方面來闡述筆者借助概念圖在開展教學設計中的應用、實踐與思考.

1 基于概念圖的初中數學教學設計的實踐

1.1 教材研究

教師獨立開展教學設計，在教學設計中揣摩教材的編寫意圖，把握教材，對教學內容進行精選和有效整合，合理選擇教學策略，編擬教學設計，從而增強自我研究能力.本節課是“圓的對稱性”第一節新授課，通過鉆研教材，筆者發現中心對稱性的知識與疊合的方法是學習本節課的基礎.為此，筆者通過概念圖中的知識準備與方法準備來設計教學.

環節1：情境創設，提出問題.

（1）摩天輪繞固定軸心旋轉180°，它都與初始位置重合嗎？摩天輪繞固定軸心旋轉任意角度，它都與初始位置重合嗎？（2）回顧上節課所學內容，什么是等弧？用什么方法驗證兩條弧是等弧？

設計意圖：通過復習中心對稱圖形為本節課內容作鋪墊.接著通過圓繞圓心的旋轉感受它的旋轉不變性.在此過程中使用疊合的方法，為本節課的學法指導作了鋪墊.

環節2：第一個實踐探索——操作、猜想、證明.

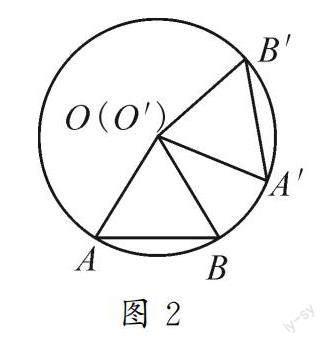
（1）在兩張透明紙片上，分別作半徑相等的⊙O和⊙O′.（2）在⊙O和⊙O′中，分別作相等的圓心角∠AOB，∠A′O′B′，連接AB，A′B′.（3）將兩張紙片疊在一起，使⊙O與⊙O′重合（如圖2）.

（4）固定圓心，將其中一個圓旋轉某個角度，使得OA與OA′重合.你發現了什么？請與同學們交流.

設計意圖：引導學生經歷“操作—觀察—猜想—說理”的過程，旨在讓學生通過自主探究和合作交流探索圓心角定理，感受圓心角、弧、弦之間的關系.引導學生用三種語言掌握，尤其是符號語言.

說明：概念圖可以使教師從整體上把握所教內容.但上課時每個環節之間的過渡只有通過精細化的預設，才能更好地啟發學生進行下一環節.例如，情境創設之后的引入語——下面我們用圓的中心對稱性和疊合法來探究本節課的內容.完成實踐探索之后的引入語——借助“蛋筒模型”來感受，在同圓或等圓中，等弧、等弦、相等的圓心角之間可以相互轉化.相等的圓心角轉化為相等的弧.于是可以得到“在同圓或等圓中，圓心角的度數與它所對的弧的度數相等”.小結反思環節后的引入語——本節課我們用圓的旋轉不變性和疊合法來探究了相關性質，下節課我們用軸對稱性和疊合法共同探究圓的垂徑定理.

過渡性語言起到承上啟下的作用，引導學生體會前后知識的聯系，對于概念圖教學發揮著重要作用.

1.2 “學生”研究

上課不是簡單地將教材內容傳授給學生，也不是學生配合教師完成任務，而是引導學生進行經驗改造，用教材所體現的經驗來豐富、發展學生的已有經驗.在備課時，筆者會設身處地站在學生的角度來思考怎樣學習才能更有效.只有關注學生需要的教學，才有助于發揮學生學習的主體性及增強學生學習的責任感，促進學生自主發展.圍繞概念圖中知識方面、技能方面、數學思想，筆者精心設計問題導入.

環節3：第一個實踐探索環節的變式.

（1）在同圓或等圓中，如果圓心角所對的弧相等，那么它們所對的弦相等嗎？這兩個圓心角相等嗎？為什么？（2）在同圓或等圓中，如果圓心角所對的弦相等，那么它們所對的弧相等嗎？這兩個圓心角相等嗎？為什么？

設計意圖：引導學生經歷“操作—觀察—猜想—說理”的過程，旨在讓學生通過自主探究和合作交流探索圓心角、弧、弦之間的關系.為探索圓心角、弧、弦之間的關系，共提出兩個問題，學生在解決第一個問題后，會積累一定的經驗與方法，為后面問題的解決提供幫助.在探究過程中，采用“疊合法”說明兩條弧相等.通過思考、探索，得出相應的結論并嘗試說理，鼓勵學生用多種方法和手段進行探究.圓心角定理及其推論生成之后引導學生用三種語言掌握，尤其是符號語言.另外，通過“蛋筒模型”引導學生更形象地理解、記憶和掌握等弧、等弦、等圓心角的相互轉化.

這樣引導學生自主探索，激發思維，前后銜接緊密.學生也會因為探索目標明確而動力十足.

以問題為切入點的設置符合學生的認知規律，但是如果只是簡單地將問題擺出，而沒有提示學生后面的問題與第一個問題之間的關系，學生的探索過程難免會割裂整個知識生成過程的完整性.為此，筆者在第一個問題提出后先設置這樣的問題：如果將問題（1）中的條件與其中一個結論互換位置，得到的命題正確嗎？你能寫出推理過程嗎？史寧中教授曾經說過：“幾何教學要注重原型啟發.”為了能讓學生更好地使用這三個定理，自如轉化“弧、弦、角”三個等量.筆者預設了“蛋筒模型”的圖片，引導學生借助生活中的圖片來形象理解數學概念及相關轉化，觀察模型中對應的弧、弦、圓心角，感受在同圓或等圓中，等弧、等弦、等圓心角可以相互轉化.

1.3 教法研究

古代教育家孔子將啟發式教學概括為“不憤不啟，不悱不發”.教師的“啟”是為了促進學生的“思”.圖1中圓心角定理及其推論的三種語言的表達要借助于數學活動來實現，而數學活動的開展要依賴于小組合作.為了能讓學生更好地參與到數學活動中去，備教法時，筆者在設計過程中堅持啟發式的教學方法，通過設計問題、解決問題，進行師生互動、生生交流，啟發學生感悟知識的生成過程.

上課時，若教師處理不當，往往會出現如下情況：如學生被動的參與多，主動的參與少，即學生的參與只是對教師要求的應對，而不是自主的表現.學生的淺層性參與多，深層性參與少，即學生的參與主要基于教材的知識與答案，而不是基于自己個性化思考的質疑，這種參與沒有帶來智慧，更談不上學會深度學習.深度學習是學習者以高階思維的發展和實際問題的解決為目標，以整合的知識為內容，積極主動地、批判地學習新的知識和思想，并將它們融入到原有的認知結構中，且能將已有的知識遷移到新的情境中的一種學習.

下面結合本節課的授課片斷，體現筆者是如何開展學生的深度學習的.

師：下面我們小結一下，在同圓或等圓中，相等的兩弧所對的兩弦、兩圓心角相等嗎？（大多數同學躍躍欲試.）

生1：相等.

師：真棒！在同圓或等圓中，相等的兩弦所對的圓心角相等嗎？兩等弦所對的劣弧相等嗎？

生2：相等.（大多數學生先用手比劃.）

生3：我們還能得到：在同圓或等圓中，兩個相等的圓心角所對的兩條弧、兩條弦相等.

師：太棒了！兩等弧、兩等弦、兩等圓心角在同圓或等圓中是可以相互轉化的.為了更好地理解、記憶，你能否用生活中的實物模型來展示它們呢？

學生先是沉默，但眼珠在轉動，手指在比劃，接著聲音就大起來了.

生4：蛋筒.（投影展示）這是我剛畫出的兩個蛋筒模型，下面部分可以看作兩圓心角……

師：你真有數學眼光，想象力很豐富.

為了能讓學生更主動地參與，更主動地進行高階思維、深度思考，即進行自主性、探究性學習及合作性學習，教師應當讓學生“有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程”，這也是《義務教育數學課程標準（2022年版）》提出的要求.衡量教學是否采用了先進的教法，關鍵看是否啟發了學生的思維，讓學生真正成為學習的主人.

環節4：第二個實踐探索環節.

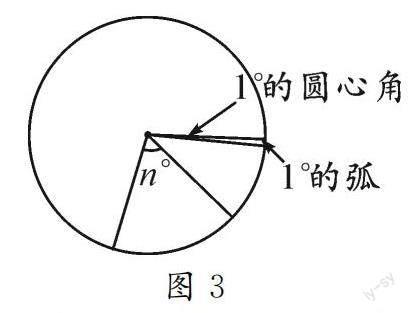
如圖3所示，1°的圓心角對應1°的弧，n°的圓心角對應n°的弧，n°的弧對應n°的圓心角.思考：圓心角的度數與它所對的弧的度數相等嗎？

設計意圖：鞏固圓心角定理，在同圓或等圓中，把相等的圓心角轉化為相等的弧是圓心角定理的應用和內化.在學習過程中，將剛學過的定理遷移到新的情境中，引導學生自主、探究性地深度學習，積累數學活動經驗.

2 基于概念圖開展初中數學教學設計的思考

2.1 整體把握教學設計

使用概念圖可以幫助教師從整體上把握本節課的知識要點、脈絡、框架，對教材進行深度分析；超越教材從“雙基”到“四基”，培養學生從“二能”到“四能”；從多個維度把握教材的完整內涵.從文字到符號的理解建構，讓學生從知識到素養內化提升，真是“會當凌絕頂，一覽眾山小”.利用概念圖，可以提示教師在上課時使用過渡性語言的時機，進而更自信、更淡定地面對每個學生，同時會讓學生感受到教師清晰的上課思路.

2.2 充分考慮學生學情

美國著名心理學家奧蘇泊爾指出：“影響學習的唯一重要的因素，就是學習者已經知道了什么.”學生學情的深度分析主要從以下三個方面入手：一是學生的前理解.分析學生的先知、先驗，從中定位學生有可能存在的困難之處，進而尋找解決策略.二是學生的內源性.分析學生的興趣、思維、情感的需要，從中定位學生興趣的引發處、思維的生長點和情感的共鳴處.三是學生的發展區.分析學生的最近發展區，從中定位學生的發展層次水平，進而選擇例題、習題及講授方式.上節課，學生學習了圓的基本概念，已經運用疊合的操作活動探究了軸對稱、中心對稱等知識，積累了相關的數學基本活動經驗.本節課的設計在此基礎上，主要讓學生充分動手操作、觀察、猜想、驗證、說理，發展學生的語言表達能力和思維能力.

2.3 創“模型圖”，助力“三會”

設計教學時，筆者創造了“蛋筒”這個模型圖.這個模型很形象，它便于學生理解弧、弦、角三者間的相互轉化，而且深化了記憶；助推學生形象思維向抽象思維的過渡，讓推理過程可視化，加深了知識概念圖的生成.創造性地使用模型圖，可以降低知識應用的難度.使用模型圖，學生“想圖形、說推理”，更容易用符號有條理地表達，進而逐步引導學生學會“用數學的思維思考世界，用數學的語言表達世界”.

2.4 設問題串，遷移經驗

蘇格拉底曾說：“最好的教學方法不是給他們成功的答案，而是向他們提問題.”指向學生關鍵能力和必備品格的問題一定是有價值的問題，它關聯著教材的核心概念.

課后專家們的評課也印證了筆者的一些預設：本節課的教學環節清楚，教師語言過渡自然；教師從實際生活中的場景入手，激發學生的學習興趣，再通過有目的的操作探究、合作交流、成果展示，啟發學生推導、直觀體驗圓心角定理及其推論；注重數學思考和問題解決，教師設計了一連串的問題，通過不斷的提問，問思路、問道理，及時組織學生交流思維過程，提供思考問題的方法，展現解決問題的途徑.

因此，分析教材、學情、教法，巧用過渡性語言及設置問題串是使用“概念圖”開展教學設計要考慮的要素.創造實物模型輔助學生形象地理解，因而突破了重難點，體現了深度教學設計的理念.嘗試使用“概念圖”備課，啟發學生深入挖掘知識“節點”的內涵及知識“節點”間的聯系，引導學生從符號學習走向學科思想和意義系統的建構，培養學生的創新思維和問題解決的能力，提升數學核心素養.

參考文獻：

［1］袁健.指向數學學科核心素養的概念圖教學設計模式探究［J］.中學數學，2021（2）：13-15.

［1］曹一鳴.數學教學設計與實施［M］.北京：北京師范大學出版社，2021.

［2］中華人民共和國教育部.義務教育數學課程標準（2011年版）［S］.北京：北京師范大學出版社，2011.

［4］李松林，賀慧，張燕.深度學習究竟是什么樣的學習［J］.教育科學研究，2018（10）：54-58.