數形結合思想在二次函數問題中的巧用

謝成強

【摘? 要】? 二次函數的圖象與性質是中考的必考內容.二次函數是數形結合的好素材，考查學生畫圖、識圖、用圖的能力，考查學生數據處理能力和數學運算能力.

【關鍵詞】? 初中數學；數形結合；二次函數

二次函數是中學數學的重要內容，其很多性質都在圖象上得以呈現.正如華羅庚說“數無形時少直覺，形少數時難入微”，二次函數的圖象會告訴我們二次函數系數之間的關系以及更多的有用信息.本文分類剖析數形結合思想在二次函數問題中的應用.

1? 利用二次函數圖象求參數范圍

例1? （2022·四川南充）已知點在拋物線上，當且時，都有，則m的取值范圍為（? ?）

（A）. （B）. （C）. （D）.

分析? 根據題意可得，拋物線的對稱軸為，然后分四種情況進行討論分析，最后進行綜合即可得出結果．

解析? 根據題意可得，拋物線的對稱軸為，

①當0<m<時，恒成立；

②當時，恒不成立；

③當時，使恒成立，

∴m，

∴m，，

④當時，恒不成立；

綜上可得：，故選（A）．

點評? 本題考查拋物線與點的關系，考查二次函數的基本性質，學會從題目中提取有用信息，熟練掌握二次函數的基本性質是解決本題的關鍵．

2? 利用二次函數圖象解決代數式的最值問題

例2? （2022·涼山州）已知實數a、b滿足a﹣b2＝4，則代數式a2﹣3b2+a﹣14的最小值是? ? ?．

分析? 根據a﹣b2＝4得出b2＝a﹣4，代入代數式a2﹣3b2+a﹣14中，然后結合二次函數的性質即可得到答案．

解析? ∵a﹣b2＝4，

∴b2＝a﹣4，

∴原式＝a2﹣3（a﹣4）+a﹣14

＝a2﹣3a+12+a﹣14

＝a2﹣2a﹣2

＝a2﹣2a+1﹣1﹣2

＝（a﹣1）2﹣3.

∵1＞0，

又∵b2＝a﹣4≥0，

∴a≥4，

∵1＞0，

∴當a≥4時，原式的值隨著a的增大而增大，

∴當a＝4時，原式取最小值為6，

故答案為：6．

點評? 本題巧妙之處就在于：從求代數式的最值問題聯想到二次函數的最值．解題的關鍵是靈活掌握配方法，熟練運用代數式的性質，完成本題．

3? 利用函數圖象確定其他函數圖象

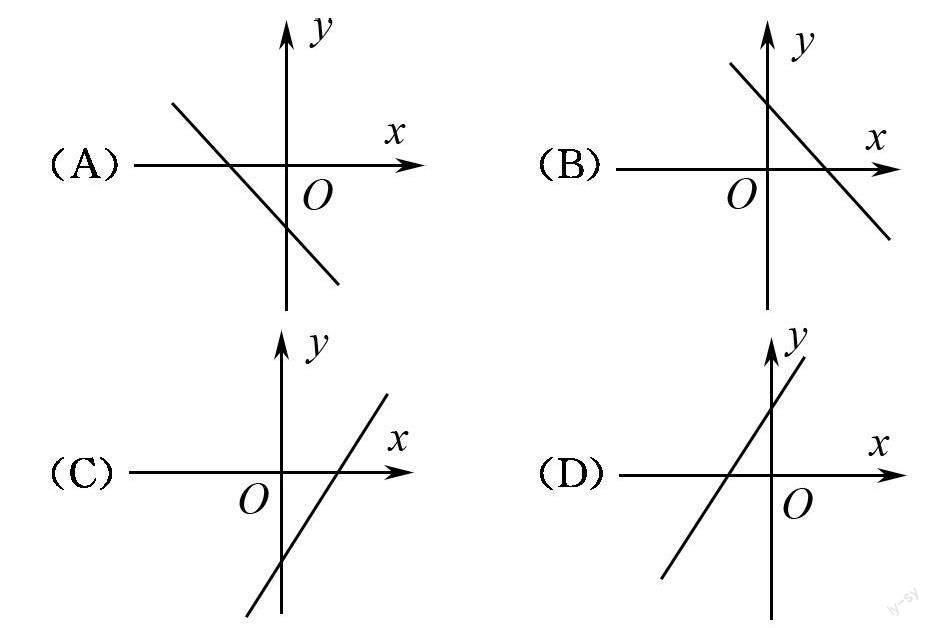
例3? （2020自貢）函數與y＝ax2+bx+c的圖象如圖1所示，則函數y＝kx﹣b的大致圖象為（? ?）

圖1

（A）（B）（C）（D）

分析? 先利用已知圖中的反比例圖象判斷k的符號，利用二次函數圖象判斷b的符號，即可判斷正誤.

解析 根據反比例函數的圖象位于一、三象限知k＞0，

根據二次函數的圖象，知a＜0，b＜0，

∴函數y＝kx﹣b的大致圖象經過一、二、三象限，

因此本題選（D）．

點評? 本題考查了反比例、一次函數、二次函數的圖象與性質等知識，考查二次函數的頂點坐標、開口方向和對稱軸等．

4? 利用兩個圖象的交點個數求參數范圍

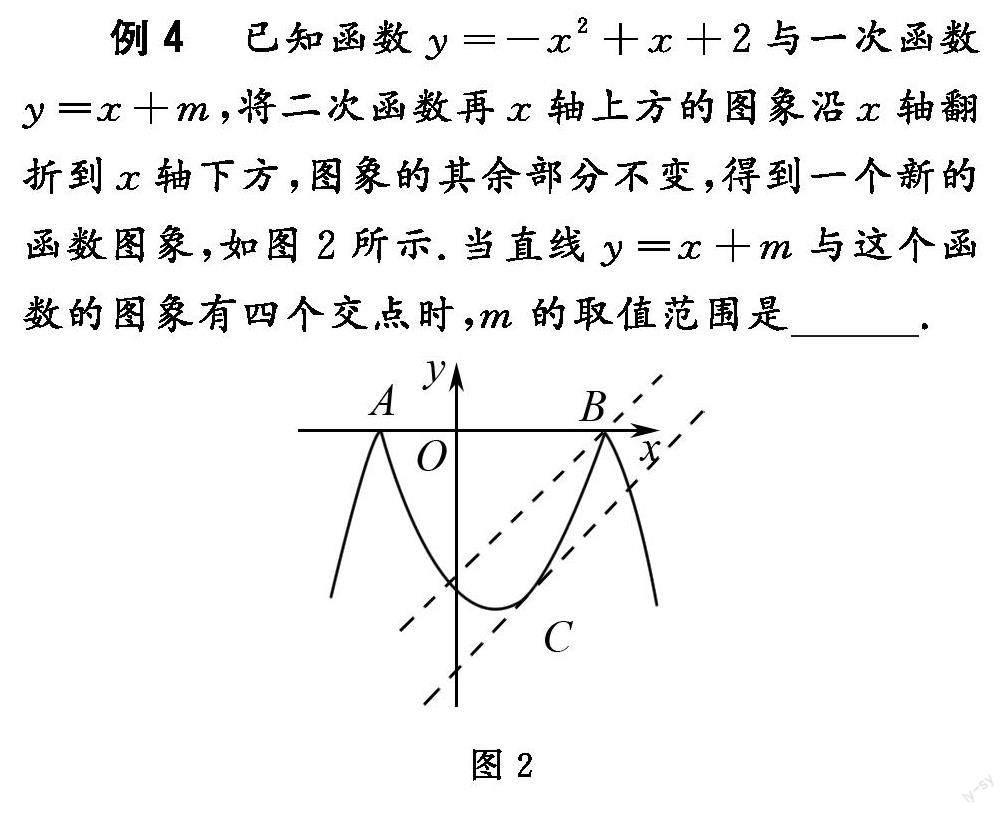
例4? 已知函數y＝-｜﹣x2+x+2｜與一次函數y＝x+m，當直線y＝x+m與這個函數的圖象有四個交點時，m的取值范圍是_______．

分析? 函數y＝-｜﹣x2+x+2｜的圖象是將二次函數y＝﹣x2+x+2在x軸上方的圖象沿x軸翻折到x軸下方，圖象的其余部分不變，得到一個新的函數圖象，如圖2所示，過點B作直線y＝x+m1，將直線向下平移到恰在點C處相切，則一次函數y＝x+m在兩條直線之間時，兩個圖象有4個交點，即可求解．

解析? 如圖所示，過點B作直線y＝x+m1，將直線向下平移到恰在點C處相切，

則一次函數y＝x+m在兩條直線之間時，兩個圖象有4個交點，

令y＝﹣x2+x+2＝0，解得：x＝﹣1或2，即點B坐標（2，0），

翻折拋物線的表達式為：y＝（x﹣2）（x+1）＝x2﹣x﹣2，

將一次函數與二次函數表達式聯立并整理得：x2﹣2x﹣2﹣m＝0，

由Δ＝b2﹣4ac＝4+4（2+m）＝0，解得：m＝﹣3，

當一次函數過點B時，將點B坐標代入y＝x+m，得0＝2+m，則m＝﹣2.

點評? 本題是二次函數圖象與其他函數圖象相結合問題，解決此問題時，先作出函數圖象，結合兩個函數的圖象，求解參數范圍.

5? 由二次函數圖象判斷二次函數系數關系

例5? （2022·湖北隨州）如圖3，已知開口向下的拋物線與x軸交于點對稱軸為直線．則下列結論：①；②；③函數的最大值為；④若關于x的方數無實數根，則．正確的有（? ?）

圖3

（A）1個.? （B）2個.? （C）3個.? （D）4個.

分析? 根據二次函數的圖象，結合二次函數的對稱軸和頂點坐標的性質得出a，b，c的關系.

解析? 由圖象可知，圖象開口向下，a＜0，對稱軸為x=1，故，故b＞0，且，則，故②正確.

∵圖象與y軸的交點為正半軸，∴c＞0，則abc＜0，故①錯誤.

由圖象可知當x=1時，函數取最大值，將x=1，代入，中得：，

由圖象可知函數與x軸交點為（﹣1，0），對稱軸為x=1，故函數圖象與x軸的另一交點為（3，0），

設函數解析式為：，

將交點坐標代入得：，故化簡得：，

將x=1，代入可得：，故函數的最大值為-4a，故③正確.

變形為：要使方程無實數根，

則，將c=-3a，，代入得：，

因為a＜0，則，則，

綜上所述，因此④正確.

所以②③④正確，故選（C）．

點評? 本題主要考查二次函數的交點式和一般式，同時考查二次函數的最值，對稱軸及交點坐標，數形結合思想化解本題的難點．根據二次函數的圖象與性質，對四個結論逐一判斷即可.