核心素養視域下的單元教學

薛彩霞

［摘 要］文章以蘇教版小學數學四年級下冊“運算律”單元學習為例，闡述核心素養視域下的單元教學策略，通過單元目標的制訂、教學內容的整合、單元學習主題的確定，全面深化學生對運算律的認識。

［關鍵詞］運算律；單元教學；核心素養

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2024）05-0049-04

在核心素養視域下，以主題引領單元教學，要做到：1.目標制訂，建立核心素養導向的學習目標，選擇與主題相匹配的核心素養表現；2.主題確定，結構化整合教學內容，遵循數學學科邏輯和學生學習邏輯；3.解決問題，綜合本學科知識和方法運用，綜合運用數學與其他學科的知識和方法解決實際問題。另外，在教學中還要遵循學生的認知規律，不斷調整和優化主題探究的進程，以此促進數學課程育人方式和學生學習方式的變革。

運算律，即運算的規律。加法和乘法的計算過程蘊含著具有普遍意義的規律。在計算過程中，學生可以通過演繹推理，將這些規律運用于具體計算。在運算律的教學過程中，教師要引導學生關注數學深層次的潛在結構，并用符號表達這種具有一般性的規律，以提升學生數學思維能力。

一、單元內容分析

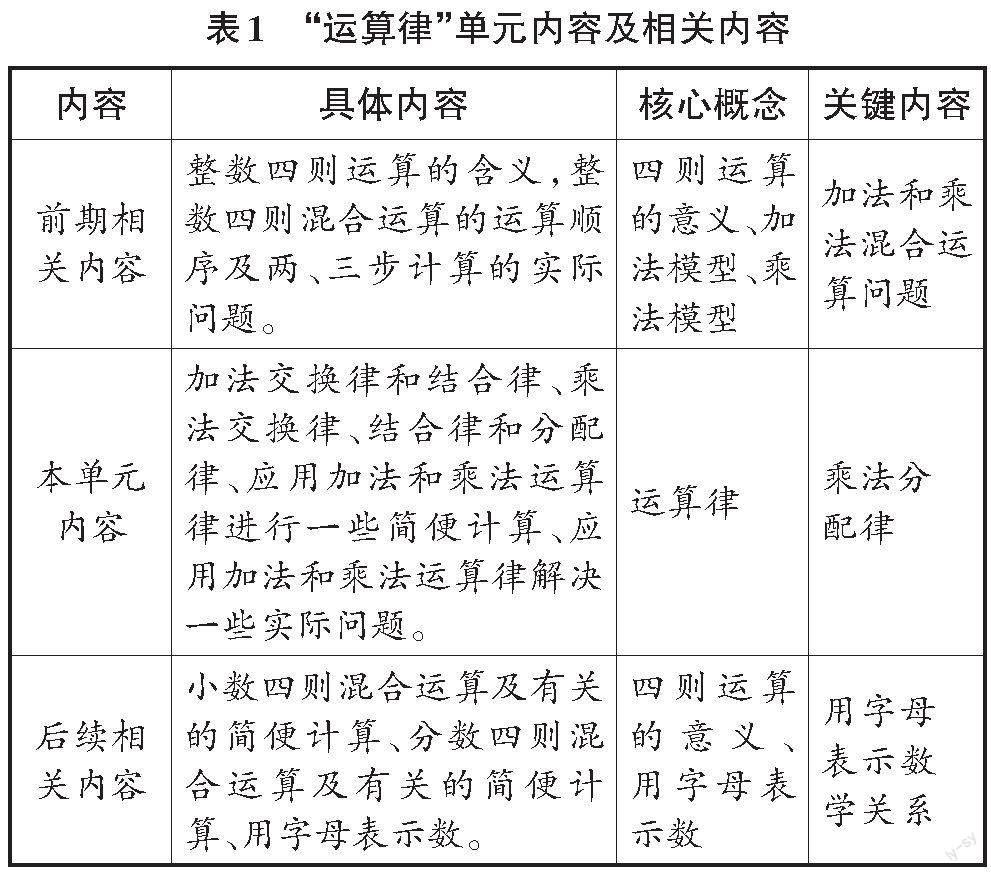
“運算律”單元內容及相關內容見表1。

（一）目標制訂指向核心素養

《義務教育數學課程標準（2022年版）》（以下簡稱《課程標準》）對運算律的內容要求是：探索并理解運算律（加法交換律和結合律、乘法交換律和結合律、乘法對加法的分配律），能用字母表示運算律。以此為基礎，基于“教—學—評”一致性教學理念，筆者從學業要求、具體表現、素養指向三個方面，制訂了單元學習目標（見表2）。

對學業要求，從“教”的角度入手，明確學生需要掌握的知識技能；對具體表現，從“學”的角度入手，細化學生探究的具體行為表征；對素養指向，從“評”的角度入手，掌握學生學習過程中核心素養的具體表現。單元學習目標從學業要求、具體表現、素養指向三個方面進行分析解讀，更具體、操作性更強，讓教師的“教”和學生的“學”更適切。

（二）教學內容結構化整合

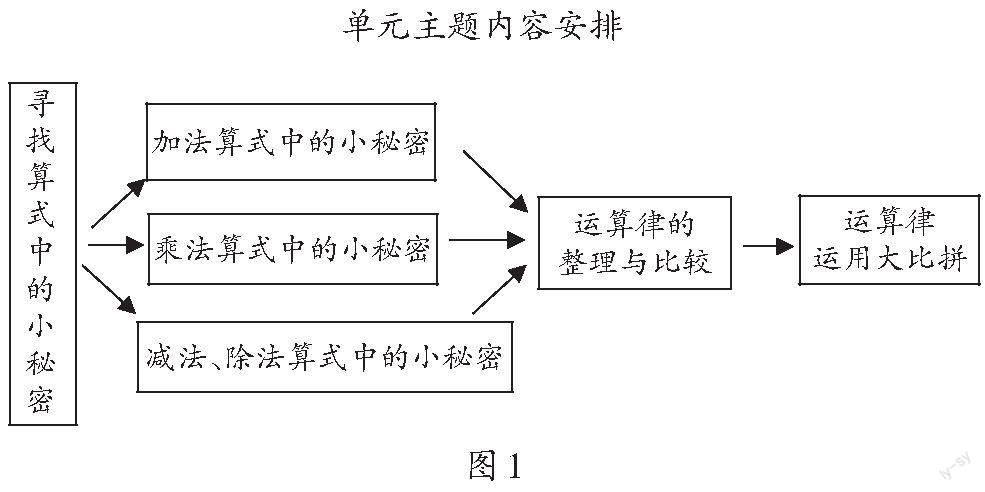
基于兒童立場，由“生活邏輯”和“學科邏輯”生成“學習邏輯”。筆者依據課程標準理念和課程內容，設計單元主題“尋找算式中的小秘密”（如圖1），并將單元主題進行拆解，降低學生的學習難度。

通過主題引領，整體建構單元知識，并通過對學習過程的回顧反思，促進學生形成對核心知識和學習歷程的深刻理解，培養學生解決問題、溝通與合作等重要能力，發展學生的批判性思維。

（三）主題引領情境化設計

《課程標準》對運算律內容的教學提示是：通過實際問題和具體計算，引導學生用歸納的方法探索運算律、用字母表示運算律，感知運算律是確定算理和算法的重要依據，形成初步的代數思維。

筆者在教學中利用校外實踐基地“開心農場”，結合“尋找算式中的小秘密”這一單元主題，通過信息技術的運用，創設農場探險活動情境。通過開展農場探險活動，讓學生在合作探究中，進行深入持續的規律探索，在富有挑戰性的情境活動中，調動現有的知識、能力、經驗等創造性地解決問題，從而達到培養學生核心素養的目的。

二、教學實踐

（一）經歷“猜想—驗證”的過程，使推理有序

運算律的學習過程通常是：解決一個實際問題—看到一個數學現象—進行類似的試驗推理—從眾多案例中抽象概括—用符號表示所發現的規律。以加法交換律為例。

1.學習例題，初步發現問題

師：操場上有28個男生跳繩，17個女生跳繩，23個女生踢毽子，一共有多少人跳繩？

生1：28+17=45（人），一共有45人跳繩。

生2：17+28=45（人），一共有45人跳繩。

師：這兩個算式有什么關系？

生3：結果相等。

2.小組討論，說理“相等”

師：用多種方式證明28+17=17+28。

生4：可以結合實際問題來證明。28+17和17+28都是求跳繩的人數，所以兩個算式的結果相同。

生5：可以通過計算證明。因為28+17=45，17+28=45，所以28+17=17+28。

生6：可以通過畫線段圖（如圖2）來證明。

生7：可以利用加法的意義來證明。算式28+17和17+28都是求28和17合起來是多少，所以28+17=17+28。

3.舉例對比，總結規律

師：照樣子寫出其他類似的算式，觀察比較這些算式，你有什么發現？把你的發現用喜歡的方法表示出來。

……

通過自主探索、對比研究，學生深刻認識了加法交換律。在教學中，教師給學生留出自主探索、合作交流的時間與空間，借助豐富、有趣、高效的學習活動，引導學生充分觀察、比較、歸納、類比，有助于學生積累研究經驗、培養推理意識、提升思維能力。

（二）多種方式驗證規律，讓推理有據

如何讓抽象的思維具體化、形象化？這需要教師從數學知識的本質出發，引導學生通過數形結合的方式理解知識，降低學習難度。以乘法分配律為例。

1.以問題引導反思

（教學乘法分配律后，教師引導學生對學習過程進行回顧反思。）

師：不計算，怎樣證明（5+2）×3=5×3+2×3？

2.小組合作，多角度思考

組1：可以利用乘法的意義來證明。左邊算式（5+2）×3表示7個3相加，右邊算式5×3+2×3表示5個3加2個3，實際也是7個3相加。兩個算式都是求7個3是多少，所以結果相同。

組2：可以畫圖證明（如圖3）。兩個算式都是求圓片的總數，故兩個算式相等。

組3：可以用長方形的面積來證明。長5厘米、寬3厘米的長方形和長2厘米、寬3厘米的長方形的面積之和，與將這兩個長方形拼成一個長7厘米、寬3厘米的長方形的面積相等（如圖4），故（5+2）×3=5×3+2×3。

通過“觀察—猜想—驗證”這一過程體會乘法分配律，學生對乘法分配律的理解并不深刻。對此，教師可以進一步提出問題，讓學生通過小組合作，借助已有經驗，發揮創造力和想象力，從乘法的意義、數形結合等角度，進行驗證。通過數與形的碰撞，可以使學生鞏固對乘法分配律這一抽象數學規律的認識，深化學生對其本質的理解。

（三）回顧反思解讀算理，提升思維

運算律是整數加法和乘法計算法則的推理依據。學習中，計算教學在前，運算律教學在后，計算方法沒有從運算律進行推理。在教學運算律后，教師可以借助運算律，引導學生對已經學習過的計算法則進行再認識，促進學生對計算法則形成更深層次的理解。以乘法分配律的回顧反思為例。

師：在之前的學習中，哪些知識應用過乘法分配律？

生1：在兩位數乘一位數時有用過，如72×6的筆算（如圖5），把72各數位上的數依次與6相乘，依據的是乘法分配律。

生2：在三位數乘兩位數時也有用過，如128×16的筆算（如圖6），先把128各數位上的數依次與16各數位上的數相乘，再把兩次的計算結果相加，依據的也是乘法分配律。

通過回顧，學生經歷了用運算律解釋以往熟悉運算的算理和算法的過程，并通過數學圖式和語言解讀，體會到運算律是運算的固有規律，是確定算理算法的重要依據，加深了對運算律的理解，形成了初步的推理意識。

（四）繪制思維導圖，完善知識結構

知識是由符號表征、邏輯形式和意義三個內在要素相互關聯組成的。學生學習的過程就是將“知識”作為素材，通過感知與理解、抽象與遷移、體驗與感悟，完成自身的知識體系的架構，實現自身的成長與發展。繪制思維導圖，有利于學生把握知識之間的聯系，完善知識結構。

對“運算律”單元知識點的梳理要做到全面準確，不僅要注重對不同運算律進行分析和比較，還要注重對運算律進行分類比較。筆者引導學生繪制“運算律”單元思維導圖（如圖7），幫助學生整體構建對運算律的認識。

《課程標準》指出，數學課程要培養的學生核心素養，主要包括以下三個方面：會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界。綜上所述，核心素養視域下的單元整體教學，以教學內容的本質及其所體現的核心素養表現為統領，將具有內在一致性的知識進行整合。在單元整體教學中，教師設計單元主題，串聯各知識點，整體建構單元知識體系，能幫助學生更好地感悟數學內容的本質、關注數學內容之間的關聯，更有效地建立體現數學學科本質、對未來學習有支撐意義的結構化的數學知識體系。

［ 參 考 文 獻 ］

[1] 中華人民共和國教育部.義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022.

[2]黃欣然，喻平.布魯納認知結構學習理論對小學數學教學的啟示[J].教育研究與評論（小學教育教學），2023（1）：14-21.

[3]高嵩，陳曉端.論當代主題式教學中的課程知識整合[J].課程·教材·教法，2020，40（5）：79-86.