借助數形結合 發展幾何直觀

王衛東

摘? 要：幾何直觀是數學核心素養的主要表現之一。文章基于教學過程，逐步闡述如何借助數形結合思想，促使學生在平面直角坐標系的數形轉換的學習中，充分積累數學學習的基本活動經驗，感悟數形結合思想的魅力，發展幾何直觀能力，從而培養學生的數學核心素養。

關鍵詞：初中數學；數形結合；幾何直觀

《義務教育數學課程標準（2022年版）》關于幾何直觀的內涵是這樣表述的：幾何直觀主要是指運用圖表描述和分析問題的意識與習慣。能夠感知各種幾何圖形及其組成元素，依據圖形的特征進行分類；根據語言描述畫出相應的圖形，分析圖形的性質；建立形與數的聯系，構建數學問題的直觀模型；利用圖表分析實際情境與數學問題，探索解決問題的思路。

實數與數軸上的點一一對應的關系，使“點”與“數”有了和諧的統一。數可以用直線上的點來表示，反之直線上的點也可以用數來表示；絕對值與距離的關聯，讓點與點之間的距離可以用數來表達；平面直角坐標系的建立，讓“數”和“形”有了完美的結合。也就是說，可以用代數的方法來研究解決幾何問題，也可以從幾何的視角研究解決代數問題。初中階段，數形結合是學生學習數學和解決數學問題的基本思想，也是培養學生幾何直觀能力的重要路徑之一。

在用代數的方法研究解決幾何圖形問題和借助幾何圖形研究解決代數問題中，平面直角坐標系是有效的數學工具，也是數形結合的平臺。在平面直角坐標系中，有序數對可以用來刻畫點的位置，還可以刻畫圖形的位置和形狀。它能描述兩個變量之間的依存關系，讓學生利用靜態的圖形研究動態的變化過程。下面以浙教版《義務教育教科書·數學》八年級上冊“4.3 坐標平面內圖形的軸對稱和平移”第1課時的教學為例，嘗試引導學生在積累基本活動經驗的過程中感悟數形結合思想的魅力，發展幾何直觀能力。

一、明方向，定內容，由形想數

為明確本節課數學問題的研究方向和學習內容，教師先展示一組能體現圖形的軸對稱、平移、旋轉變化在日常生活中應用的圖片（略），并設計一組問題鏈讓學生進行自主探究和實踐操作。

問題1：從數學應用的角度看，這些圖片所蘊含的數學知識可以分為幾類？分類的依據是什么？

問題2：分別說說軸對稱圖形和圖形的對稱軸，兩者的概念和性質各是什么？

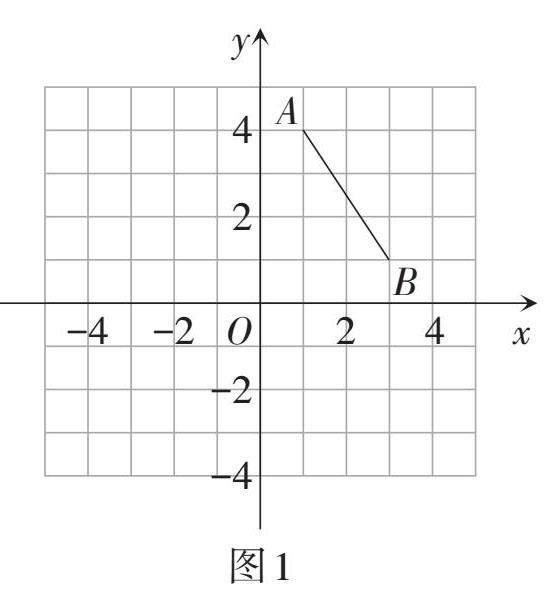
問題3：如圖1，在平面直角坐標系中作出線段AB關于y軸對稱的線段[A′B′，] 分別寫出點A，B，[A′，B′]的坐標，并觀察A，B兩點，以及與它們的對應點[A′，B′]的坐標，你有什么發現？

本環節是從日常生活的具體事例中抽象出數學知識，觸發學生已有的數學知識和經驗，通過簡單作圖和回答問題，引導學生主動參與到新知識的探究中，從而明確本節課的研究方向和學習內容。這是一個完整的數學思維過程。從觀察現實生活中的軸對稱現象，到在平面直角坐標系中作軸對稱圖形，再到寫相應的坐標及最后思考各坐標的特征，這是從幾何直觀（作圖）到代數表達的一個由“形”到“數”、發展學生幾何直觀能力的活動過程。在這個數學思維過程中，學生能夠基本確定本節課主要是研究“數”和“形”的關系。

二、引入數，升華形，由形助數

在平面直角坐標系中，研究點的變化規律是研究平面直角坐標系中圖形問題的基本路徑之一。新知識和新方法的探究應該符合低起點、小切口的原則，讓學生經歷由特殊到一般的探究過程。在問題的解決過程中，學生受限于個人的思維水平和能力差異，所獲得的經驗和抽象概括內容是不同的。因此，在學生獨立思考的基礎上，教師應該提倡合作交流，發展學生的批判思維和質疑精神。如何引導學生進行合作交流呢？這時，教師可以引入對點的坐標這種“數”的思考，讓學生在思考中得到對刻畫點在平面直角坐標系中這種“形”的深度體驗。

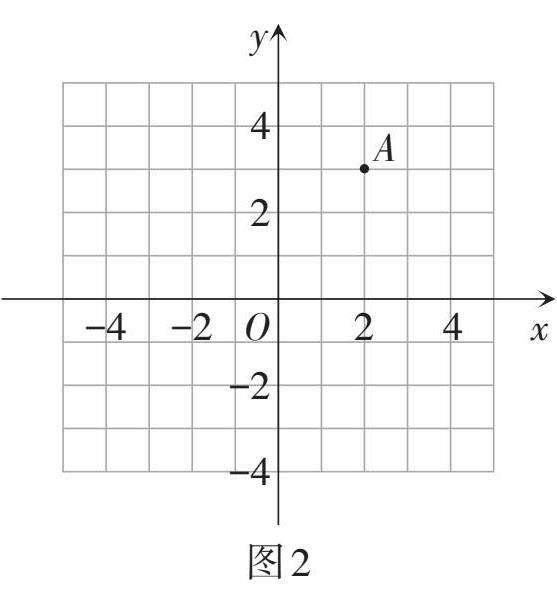
問題4：在圖2中分別作出點[A2，3]關于x軸的對稱點A1，以及關于y軸的對稱點A2，并寫出點A1，A2的坐標，比較對應點的坐標，你有什么發現？

問題5：取不同的點，再次驗證你發現的結論，并與同伴交流。

在平面直角坐標系中，點[Aa，b]關于x軸的對稱點A1的坐標為[a，-b，] 關于y軸的對稱點A2的坐標為[-a，b。] 在寫點A1，A2坐標的過程中，學生經歷了由特殊到一般的提出猜想、驗證猜想的思維過程。最后，由點的軸對稱（形）到發現點的坐標（數）規律，學生經歷了由形到數的體驗、感悟過程。在與同伴的交流過程中，學生經歷了質疑、批判、評價、決策的過程。而問題鏈的解決，是從引入“數”開始，以升華“形”結束的，是一個幾何直觀與代數表達相融合的過程，使學生體驗到了“數”和“形”是相輔相成的。

三、形助數，尋路徑，由形定數

為進一步發展學生的幾何直觀，使學生能從觀察“形”的結構特征得到“數”的表達特征，從“數”的表達特征想象“形”的結構特征，實現數形結合，這就要求教師倒推教學過程中問題鏈的設計，從而促使學生再度探究數與形的關聯，尋找解決問題的路徑。

問題6：如圖3 ，作出點[A2，3]關于直線x = -1的對稱點A1，以及關于直線y = 1的對稱點A2，并寫出點A1和A2的坐標。

問題7：在問題6中，連接AA1交直線x = -1于

點M1，連接AA2交直線y = 1于點M2，直接寫出點M1和M2的坐標。

問題8：若點[P6，2]和點[Q-2，2]關于某條直線對稱，試直接寫出該直線的表達式。

在平面直角坐標系中，點[A2，3]關于直線x = -1的對稱點A1的坐標為[-4，3，] 關于直線y = 1的對稱點A2的坐標為[2，-1。] 點[P6，2]和點[Q-2，2]關于直線x = 2對稱。因為對稱軸發生了變化，所以對稱點的坐標不再是簡單的符號變化。因此，在問題6和問題7中，學生從作出對稱點到寫出點的坐標，是對數形的淺層結合。而在問題8中，學生從根據點的坐標在平面直角坐標系中描出點，到畫出P，Q兩點的對稱軸，最后寫出對稱軸的表達式，這是一個具體可操作的可視化過程。在這個過程中，學生探究數形之間的關聯，從形中尋找數，使得數形深度結合，從而獲得一個具體的、有深度的、數形結合的活動經驗。

四、融數形，提能力，數形相融

在明確探究問題的線索和研究解決問題的方法之后，學生的學習再度走向深入。如何從點關于軸對稱的學習深入到點關于第一、三象限角平分線對稱的學習，以及由此得出任意一個線段中點坐標的學習。此時，教師應該提供關聯性知識和解決問題的問題鏈，并在問題鏈的深度挖掘中使學生鞏固數形結合思想，發展學生的幾何直觀能力。

問題9：寫出點[A2，3]關于第一、三象限角平分線對稱的點的坐標，以及點[Pa，b]關于第一、三象限角平分線對稱的點的坐標。

問題10：已知線段AB的兩個端點的坐標分別為[A4，-1，B2，3，] 試寫出線段AB的中點M的坐標，并與同伴交流你的思考過程。

有了前面解決問題的經驗，對問題9的解決，學生基本能畫出如圖4所示的圖形，從而解決問題。

對于問題10，大部分學生無從下手，少部分學生通過畫圖猜想出正確答案，但無法解釋其中的原理。此時，教師引導學生回顧并觀察問題7中點M1與點A和點A1，點M2與點A和點A2之間的坐標關系，并提出猜想，通過畫圖驗證猜想是否成立。學生立刻發現問題7中的點M1的橫坐標為[2+-42=-1，] 點M2的縱坐標為[3+-12=1，] 而點M1，M2分別是線段AA1和線段AA2的中點，于是提出初步猜想：中點橫坐標就是線段兩端點橫坐標之和的一半，中點縱坐標就是線段兩端點縱坐標之和的一半。因此，問題10中的點M的坐標是[3，1。]

對于怎樣證明猜想的準確性，學生可以利用圖形的軸對稱性質和三角形全等性質構造圖形來驗證。教師引導學生主動發現與坐標軸平行的特殊線段中點坐標與線段端點坐標存在關聯，從而引發學生猜想：一般情況下的線段中點坐標是不是也如此，并利用圖形來驗證猜想是否成立。在這個過程中，學生經歷了提出猜想、畫圖驗證、證明猜想的全過程。在與同伴的交流中，學生則經歷了批判、選擇和決策的數學思維全過程，促進數形結合，進一步發展了幾何直觀能力，培養了數學核心素養。

五、建框架，促思維，形成學習經驗

構建學習框架，是落實學生核心素養和發展學生數學思維的有效載體，是尋找解決問題的手段和方法，也是解決問題的核心環節。因此，在課堂小結環節，教師要學會放手，提供給學生思考的方向和必要的思考時間，讓學生自主進行歸納小結。關于本節課的學習，師生對以下幾個方面進行歸納小結。

（1）這節課的重點是什么？難點是什么？

（2）在平面直角坐標系中研究圖形問題時，其研究的基本對象是什么？從點關于坐標軸對稱，到關于平行于坐標軸的直線對稱，再到關于象限的角平分線對稱，最后到求平面直角坐標系中任意線段的中點坐標，在整個過程中，我們解決問題的核心方法是什么？

雖然學生的歸納各有不同，但大家對于數形結合思想、幾何直觀能力的認識達成了共識。在本節課的學習中，我們以兩條坐標軸作為對稱軸，從觀察點的坐標的變化規律入手，到如何刻畫點在平面直角坐標系中位置的“形”的思考，從而獲得原始的直接經驗；再到對稱軸為直線x = -1和直線y = 1時，感受點的坐標“數”的變與不變，深入探究變化中的不變性，從而積累活動經驗；到最后以直線y = x為對稱軸寫出對稱點的坐標，以及拓展到能在平面直角坐標系中求出任意一條線段中點的坐標，獲得理性數學經驗。數形結合思想貫穿了整個學習活動，使學生獲得了充分體驗，逐步發展了幾何直觀能力。

六、教學反思

對于本節課，如果只按照教材的課時分配進行教學，教學內容止步在點關于坐標軸對稱和作圖形關于坐標軸對稱，那么本課時的教學就只是注重教授知識，忽略了“在平面直角坐標系中研究對稱性問題”這條關鍵教學主線，也難以對后續研究二次函數圖象的軸對稱性和反比例函數圖象中心對稱進行知識關聯，很難形成系統性的知識整合。忽視初中階段研究圖形和函數圖象的軸對稱性問題，會導致學生學習數學知識體系破碎化，缺乏數學學習的連續性，限制學生的思維發展，使學生的數學學習局限于單一課時內容的學習，長遠來看不利于學生數學核心素養的發展。我們還要深度思考：這節課的教學對后續的學習能起什么作用？對學生哪方面的數學思想方法有培養和提升作用？對于幾何直觀素養的發展提供了什么樣的學習路徑？這需要教師繼續思考、實踐與提煉。

參考文獻：

［1］中華人民共和國教育部. 義務教育數學課程標準（2022年版）［M］. 北京：北京師范大學出版社，2022.

［2］趙桂芳. 加強尺規作圖? 建立幾何直觀［J］. 遼寧教育，2022（21）：5-9.