基于數(shù)學(xué)思想的空間向量與立體幾何問題的解題技巧與方法

牛曉琳

【摘要】空間向量與立體幾何作為每年高考命題中的一大主干知識(shí)，是高考數(shù)學(xué)試卷解答題中的重要類型之一.文章借助空間向量與立體幾何中的數(shù)學(xué)思想，從函數(shù)與方程思想、分類討論思想、數(shù)形結(jié)合思想等入手，通過實(shí)例剖析，闡述數(shù)學(xué)思想的應(yīng)用技巧與方式，引領(lǐng)并指導(dǎo)數(shù)學(xué)教學(xué)與復(fù)習(xí)備考.

【關(guān)鍵詞】空間向量；立體幾何；數(shù)學(xué)思想；解題應(yīng)用

引 言

空間向量與立體幾何中，重點(diǎn)是利用空間向量來解決有關(guān)的立體幾何問題，將幾何的綜合推理和向量的代數(shù)運(yùn)算有機(jī)地結(jié)合起來，為我們的數(shù)學(xué)思維活動(dòng)開辟更加廣闊的天地，更好地培養(yǎng)分析問題、解決問題的能力.在具體解決立體幾何問題的過程中，往往離不開數(shù)學(xué)思想方法的應(yīng)用.

一、函數(shù)與方程思想的應(yīng)用

在立體幾何中，通過建立空間直角坐標(biāo)系，把空間中的線段、角、距離等問題用數(shù)表示，然后通過分析變量間的對(duì)應(yīng)關(guān)系，建立方程或方程組或者構(gòu)造方程或方程組，使問題獲得解決.有關(guān)線段、角度、面積、體積的計(jì)算，經(jīng)常需要用構(gòu)造方程或建立函數(shù)關(guān)系式的方法加以解決.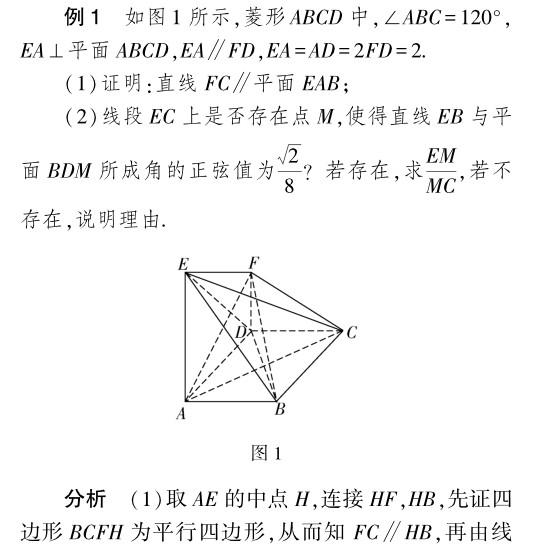

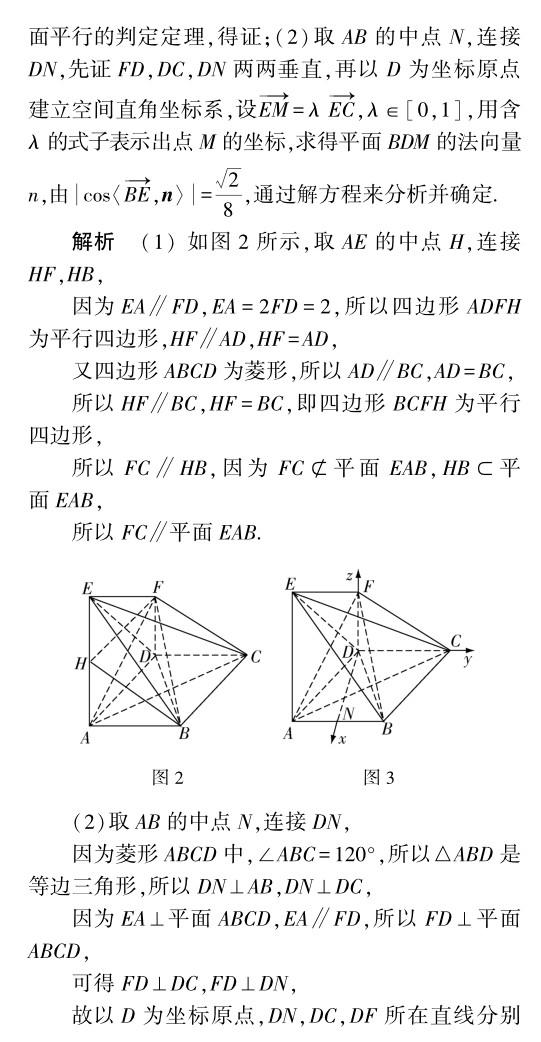
分析 （1）通過合理構(gòu)建空間直角坐標(biāo)系，設(shè)出線段CP=x，利用兩向量坐標(biāo)的確定，結(jié)合垂直關(guān)系轉(zhuǎn)化為數(shù)量積0，合理構(gòu)建對(duì)應(yīng)的關(guān)系式，再根據(jù)方程的根的個(gè)數(shù)來討論點(diǎn)的存在性問題；（2）由（1）可知a=2，進(jìn)而分別求解兩個(gè)半平面的法向量，利用數(shù)量積公式來求解對(duì)應(yīng)的二面角的平面角的余弦值即可.

解析 （1）建立如圖5所示的空間直角坐標(biāo)系，其中直線DC為x軸，直線DA為y軸，直線DD1為z軸.

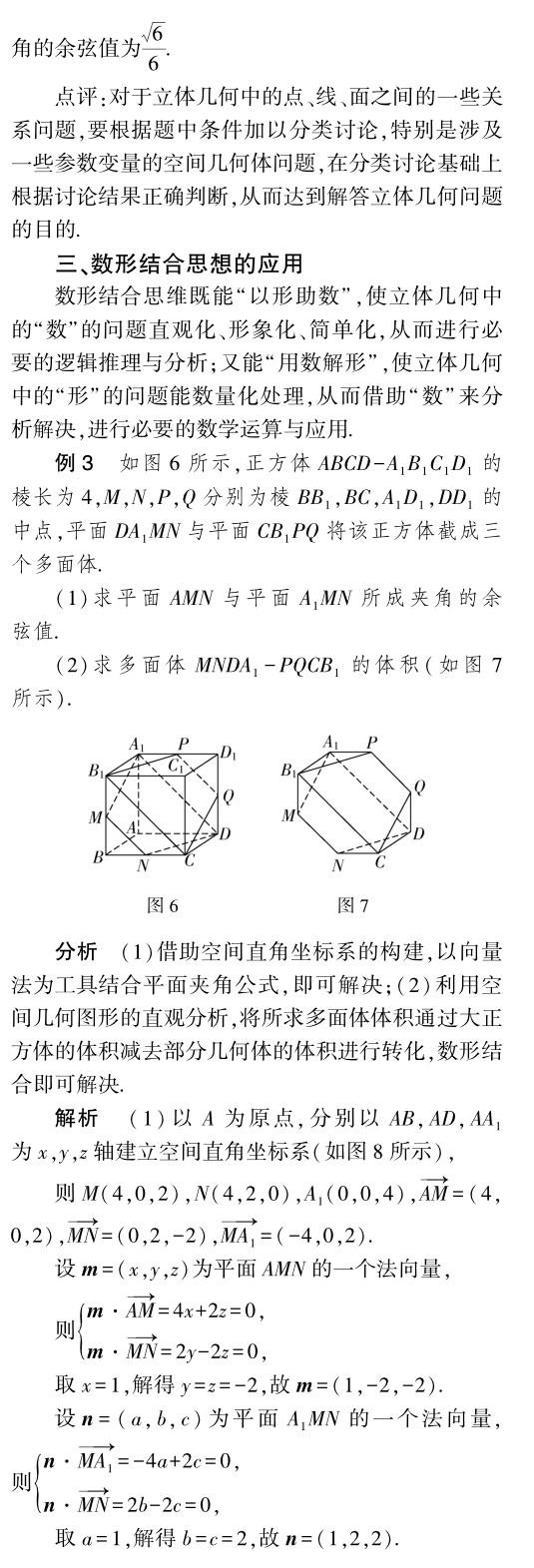
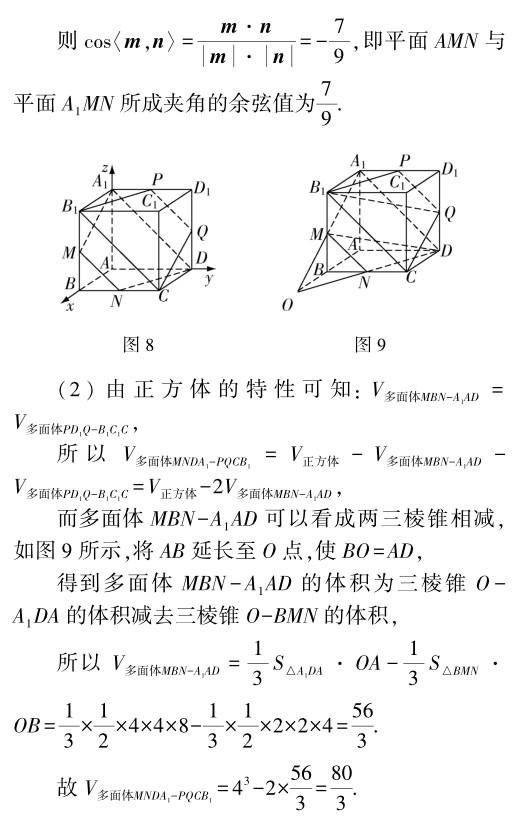
點(diǎn)評(píng)：立體幾何問題的空間想象與直觀圖形，都離不開數(shù)形結(jié)合思想的應(yīng)用，由題設(shè)條件中的“數(shù)”與“形”的信息結(jié)合，又結(jié)合邏輯推理或數(shù)學(xué)運(yùn)算這兩個(gè)層面“數(shù)”與“形”的應(yīng)用來達(dá)到目的，是解決立體幾何問題中最為常見的技巧.

結(jié) 語(yǔ)

數(shù)學(xué)思想比數(shù)學(xué)概念更具有抽象概括水平，后者比前者更具有具體性、豐富性，前者比后者更具有深刻性、拓展性.在空間向量與立體幾何的綜合問題中，結(jié)合基本知識(shí)點(diǎn)與豐富的數(shù)學(xué)思想方法的交匯與融合，總結(jié)其一般解題技巧與策略，合理應(yīng)用數(shù)學(xué)思想方法引領(lǐng)，全面提升數(shù)學(xué)思維品質(zhì)與數(shù)學(xué)基本能力，必然會(huì)達(dá)到事半功倍的良好效果.

【參考文獻(xiàn)】

[1]王婷婷.高中數(shù)學(xué)“立體幾何初步”單元教學(xué)研究[D].呼和浩特：內(nèi)蒙古師范大學(xué)，2023.

[2]張林華.活用數(shù)學(xué)化歸思想提升立幾解題能力：以2022年浙江省數(shù)學(xué)高考第19題為例[J].中學(xué)教研（數(shù)學(xué)），2022（12）：34-36.

[3]張佳媛.高中數(shù)學(xué)人教A版新舊教材“立體幾何”部分的比較研究[D].哈爾濱：哈爾濱師范大學(xué)，2021.